Содержание
- 2. Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y
- 3. y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры
- 4. 0 y x y=g (x) y=f (x) b a y = f (x), y = g
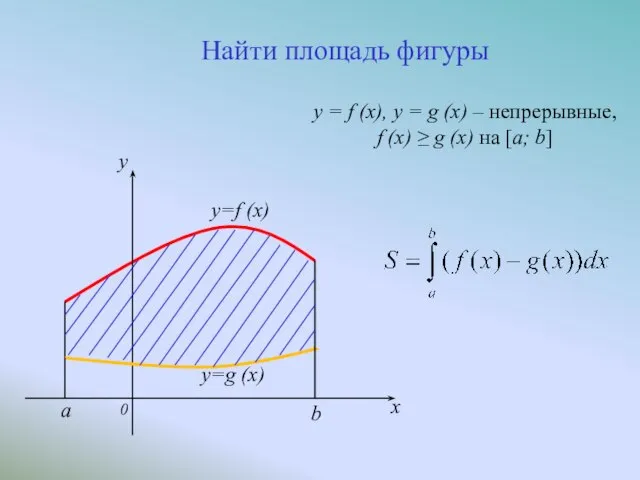
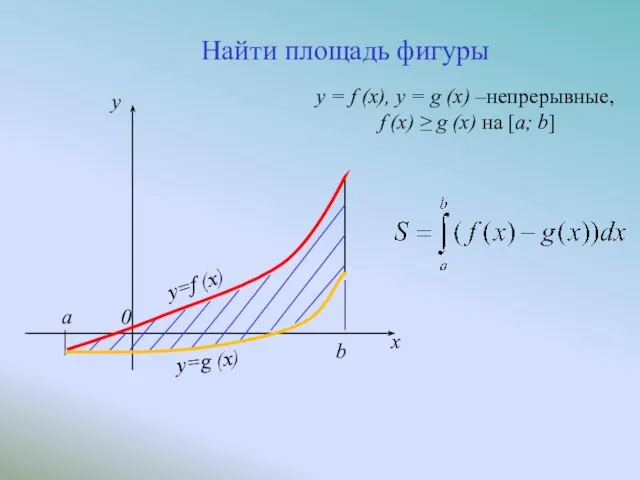
- 5. y=f (x) a y=g (x) b 0 y x Найти площадь фигуры y = f (x),
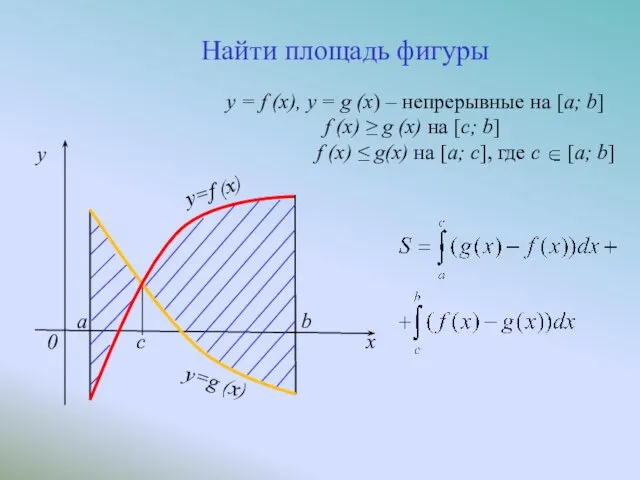
- 6. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
- 7. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
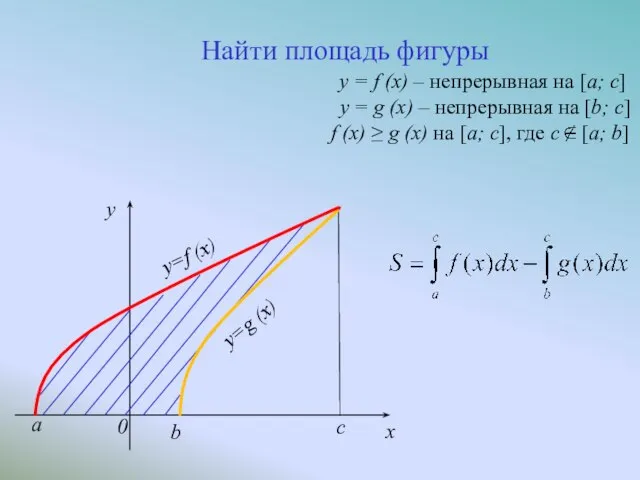
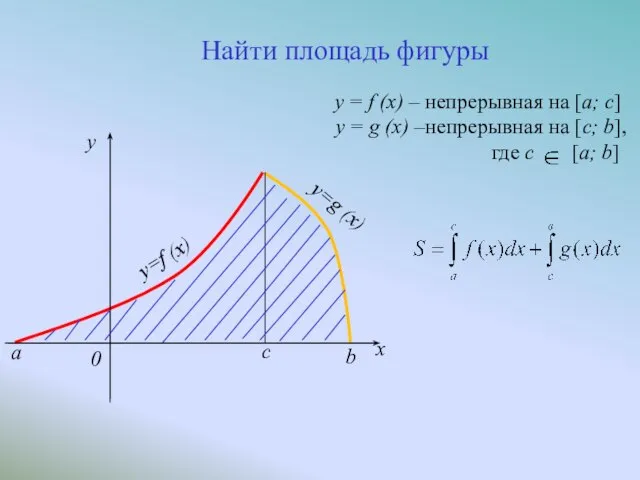
- 8. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
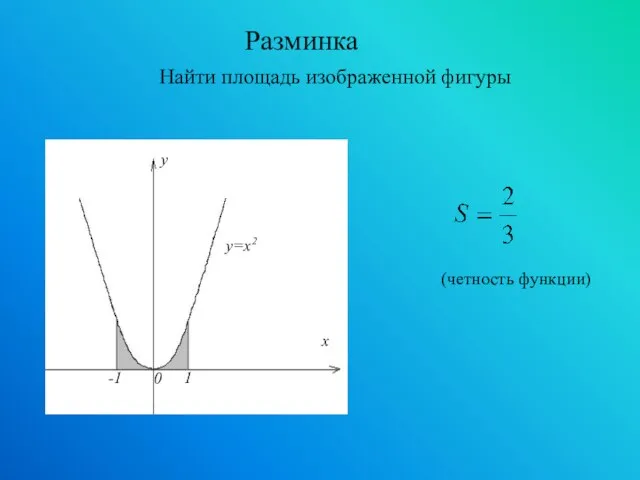
- 9. (четность функции) Разминка Найти площадь изображенной фигуры
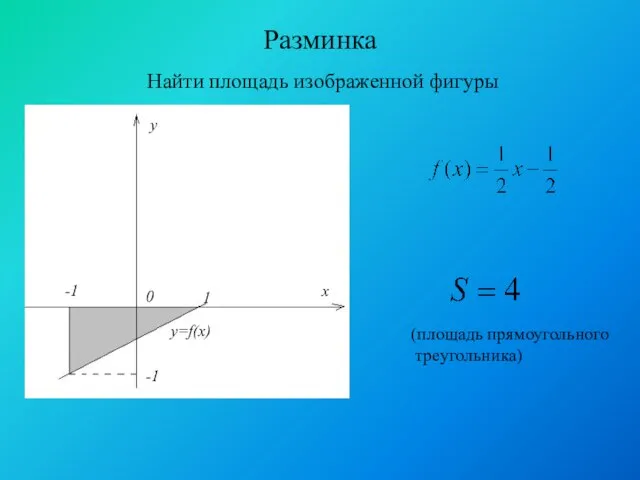
- 10. Разминка Найти площадь изображенной фигуры (площадь прямоугольного треугольника)
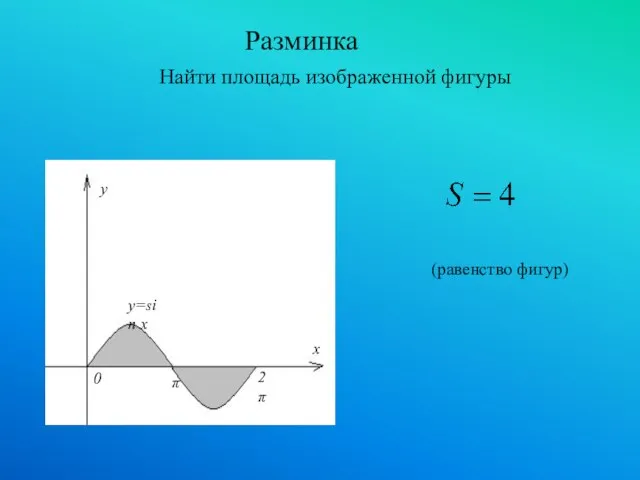
- 11. Разминка Найти площадь изображенной фигуры (равенство фигур)
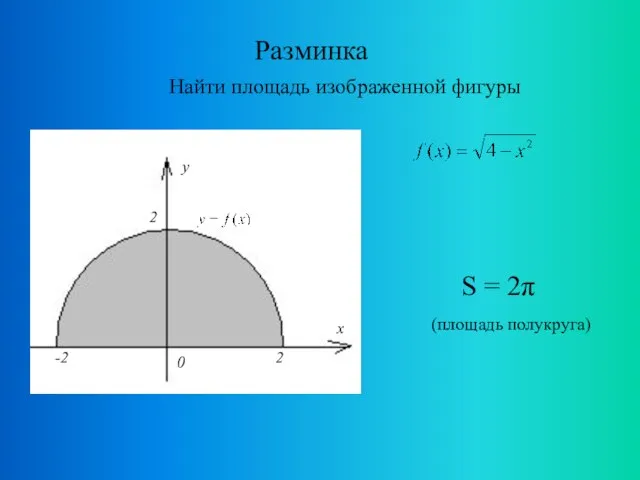
- 12. Разминка Найти площадь изображенной фигуры S = 2π (площадь полукруга)
- 13. Разминка Найти площадь изображенной фигуры S = 1 (площадь треугольника)
- 14. Задачи 1) Найти площадь фигуры, ограниченной линиями
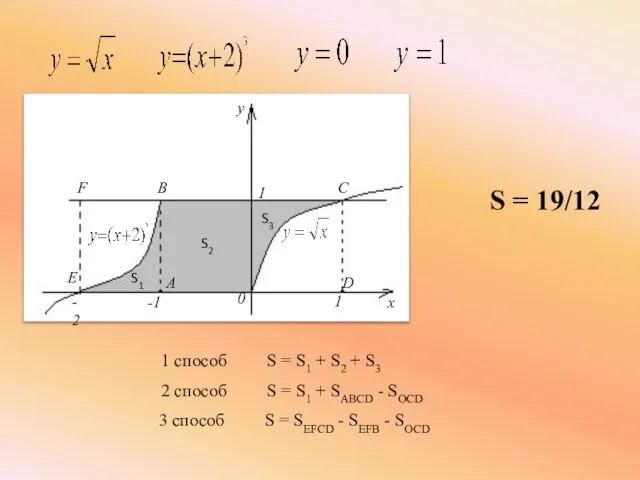
- 15. 1 способ S = S1 + S2 + S3 S = 19/12 2 способ S =
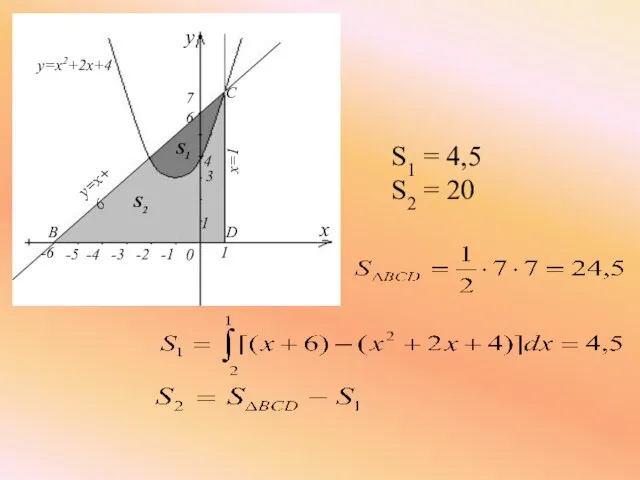
- 16. 2) Фигура, ограниченная линиями y=x+6, x=1, y=0, делится параболой y=x2 + 2x + 4 на две
- 17. S1 = 4,5 S2 = 20 1
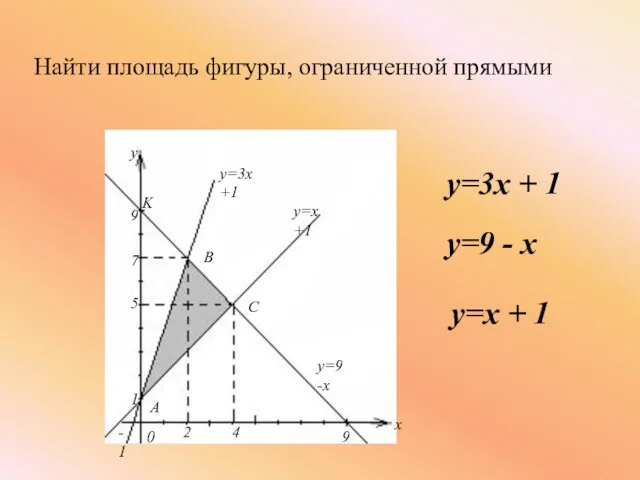
- 18. Найти площадь фигуры, ограниченной прямыми y=3x + 1 y=9 - x y=x + 1
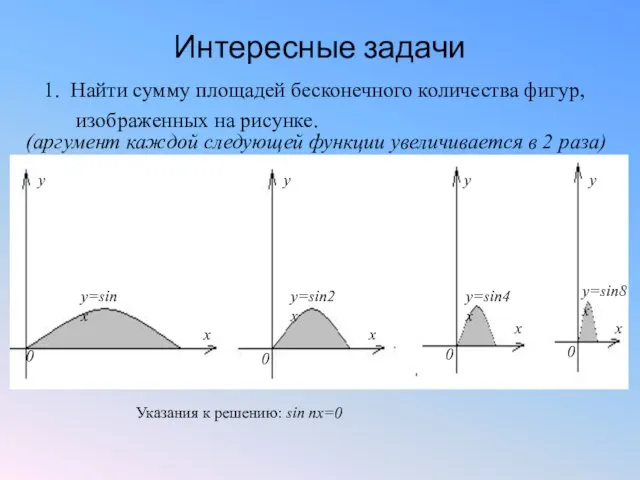
- 19. Интересные задачи 1. Найти сумму площадей бесконечного количества фигур, изображенных на рисунке. (аргумент каждой следующей функции
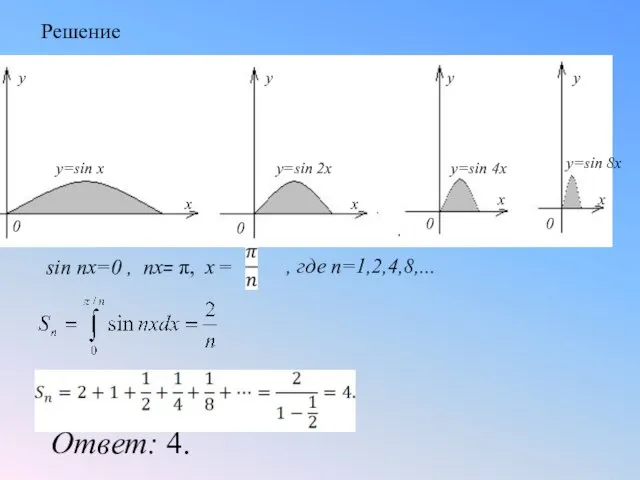
- 20. Ответ: 4. , где n=1,2,4,8,... sin nx=0 , nx= π, x = Решение
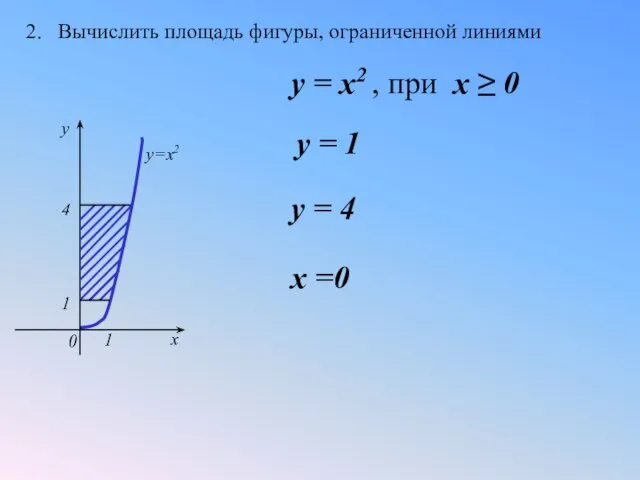
- 21. 2. Вычислить площадь фигуры, ограниченной линиями 1 1 4 0 x y y=x2 y = 1
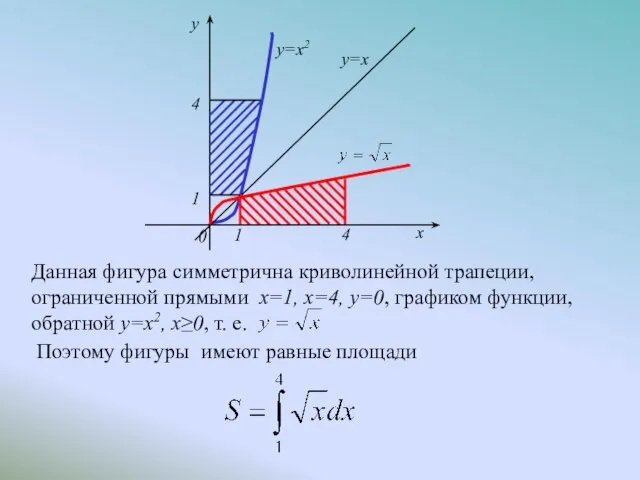
- 22. Данная фигура симметрична криволинейной трапеции, ограниченной прямыми x=1, x=4, y=0, графиком функции, обратной y=x2, x≥0, т.
- 23. Если фигура ограничена линиями x=ϕ1(y), x=ϕ2(y), y=c; y=d, где c то ее площадь может быть вычислена
- 25. Скачать презентацию
![Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/484237/slide-1.jpg)
![y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/484237/slide-2.jpg)




 Арифметические действия над положительными и отрицательными числами
Арифметические действия над положительными и отрицательными числами Презентация на тему Организационная структура системы таможенных органов РФ
Презентация на тему Организационная структура системы таможенных органов РФ Презентация на тему Даниил Заточник
Презентация на тему Даниил Заточник Мой лучший друг - математик
Мой лучший друг - математик Решение систем линейных уравнений с тремя переменными - презентация по Алгебре_
Решение систем линейных уравнений с тремя переменными - презентация по Алгебре_ Логарифмы и их свойства
Логарифмы и их свойства  В6 элементы теории вероятностей
В6 элементы теории вероятностей Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Методика обучения решению линейных неравенств с одной переменной
Методика обучения решению линейных неравенств с одной переменной Preobrazovanie-dvoynyh-radikalov.ppt
Preobrazovanie-dvoynyh-radikalov.ppt Определение производной функции y=f(x) в точке
Определение производной функции y=f(x) в точке Алгебраический тренажёр
Алгебраический тренажёр Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов
Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов  План урока
План урока Issledovanie-funkciy-i-postroenie-grafikov.ppt
Issledovanie-funkciy-i-postroenie-grafikov.ppt Урок по теме «Интеграл. Формула Ньютона-Лейбница с элентами поготовки к ЕГЭ» Учитель математики МБОУ «Колюбакинская СОШ» Смолина
Урок по теме «Интеграл. Формула Ньютона-Лейбница с элентами поготовки к ЕГЭ» Учитель математики МБОУ «Колюбакинская СОШ» Смолина Презентация на тему Основные отечественные концепции управления качеством
Презентация на тему Основные отечественные концепции управления качеством  Презентация на тему Классические типы коллизионных привязок
Презентация на тему Классические типы коллизионных привязок  primenenie-proizvodnoy-funkcii.ppt
primenenie-proizvodnoy-funkcii.ppt Степенная функция - презентация по Алгебре_
Степенная функция - презентация по Алгебре_ Logarifmicheskaya-funkciya.ppt
Logarifmicheskaya-funkciya.ppt Презентация на тему Цели и задачи прокурорского надзора
Презентация на тему Цели и задачи прокурорского надзора  Презентация на тему Суд в США
Презентация на тему Суд в США Свойства степени
Свойства степени Технологии промысловой подготовки нефти и газа
Технологии промысловой подготовки нефти и газа Презентация на тему Тест Мюнстерберга на восприятие и внимание
Презентация на тему Тест Мюнстерберга на восприятие и внимание  Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными  Теорема Виета (8 класс)
Теорема Виета (8 класс)