Metod-racionalizacii.pptx

Решение неравенств - важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные неравенства, поэтому мы решили рассмотреть один из способов решения неравенств – метод рационализации. В школьной программе он не изучается, но его применение значительно облегчает решение задания С3 ЕГЭ, в частности логарифмических и показательных неравенств.
Введение

Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:
Теоретическое
обоснование метода

Рассмотрим логарифмическое неравенство вида
, (1)
где - некоторые функции
Теорема 1.
Логарифмическое неравенство
равносильно следующей системе неравенств:
(2)
Сведение логарифмического
неравенства к системе
рациональных неравенств

Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство.
Если , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство
Если , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство
Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода.
Терема доказана.
Доказательство

Теперь рассмотрим показательное неравенство вида
3)
Так же, как в предыдущем пункте, - некоторые функции.
И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям. В первом основание степени положительно, но меньше единицы (знак неравенства обращается), во втором случае основание степени больше единицы (знак неравенства сохраняется).
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.
Сведение показательных
неравенств к системе
рациональных неравенств

Теорема 2.
Показательное неравенство
равносильно следующей системе неравенств:
(4)

Если , то первый множитель третьего неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство
.
Если , то первый множитель третьего неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство
.
Доказательство

Выделим некоторые выражения F и соответствующие им рационализирующие выражения G, где f, g, h, p, q – выражения с переменной x (h > 0,h
1, f > 0, g > 0),
1).
а – фиксированное число (a > 0, a

Доказательство
Пусть loga f- loga g> 0, то есть loga f> loga g, причём a > 0, a ≠ 1, f > 0, g > 0.
Если 0 < a < 1, то по свойству убывающей логарифмической функции имеем f < g. Значит, выполняется система неравенств
a -1<0
f – g < 0
Откуда следует неравенство (a – 1)(f – g) > 0 верное на области определения выражения F = loga f- logag.
Если a > 1, то f > g. Следовательно, имеет место неравенство (a – 1)(f – g)> 0. Обратно, если выполняется неравенство (a – 1)(f – g)> 0 на области допустимых значений (a > 0, a ≠ 1, f > 0, g > 0), то оно на этой области равносильно совокупности двух систем.
a – 1<0 a – 1 > 0
f – g < 0 f – g > 0
Из каждой системы следует неравенство loga f> loga g, то есть loga f- loga g> 0.
Аналогично, рассматриваются неравенства F < 0, F ≤ 0, F ≥ 0.

Пусть некоторое число а > 0 и а ≠ 1, тогда имеем
=
Знак последнего выражения совпадает со знаком выражения
или (h-1)(f-g) .

Так как
=
то, используя замены 2а и 2б, получаем, что знак последнего выражения совпадает со знаком выражения (f - 1)(g - 1)(h - 1)(g – f).

Из неравенства > 0 следует . Пусть число а > 1, тогда loga > loga или (h – g)loga h > 0.
Отсюда с учётом замены 1б и условия a > 1 получаем
(f – g)(a – 1)(h – 1) > 0, (f – g)(h – 1) > 0.
Аналогично, доказываются неравенства F < 0, F ≤ 0, F ≥ 0.
Доказательство проводится аналогично доказательству 4.
Доказательство замены 6 следует из равносильности неравенств | p | > | q | и p2 > q2 ( | p | < | q | и p2 < q2).

Решить неравенство:
Решение:
Пример 1.

-
-
+
+
-2
2
1
ОТВЕТ:

Решить неравенство:
Решение:
Пример 2.

-
+
-2
1
0
ОТВЕТ:
-1
-1
0
1
+
-
-
+

Решить неравенство:
Решение:
Пример 3.

Пример 4.
Решить неравенство:
Решение:

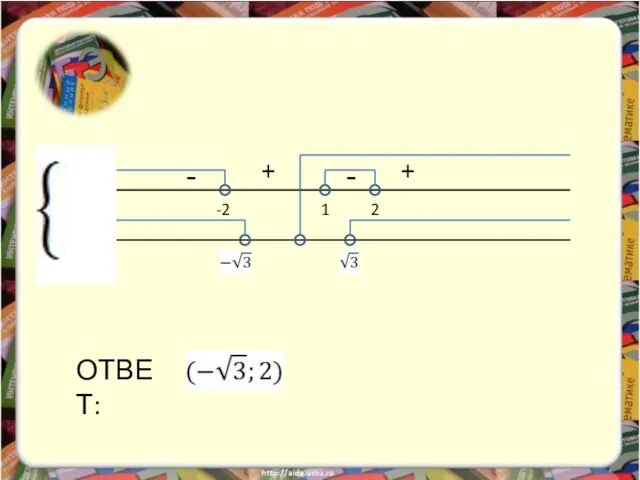
Пример 5.
Пример 6.
Пример 7.
Пример 8.
ОТВЕТ
ОТВЕТ
ОТВЕТ
ОТВЕТ
Решите примеры

Пример 9.
Пример 10.
Пример 11.
ОТВЕТ
ОТВЕТ
ОТВЕТ

-
+
1/2
3
2
ОТВЕТ:
+
-
0
-1
Пример 5
НАЗАД

-
+
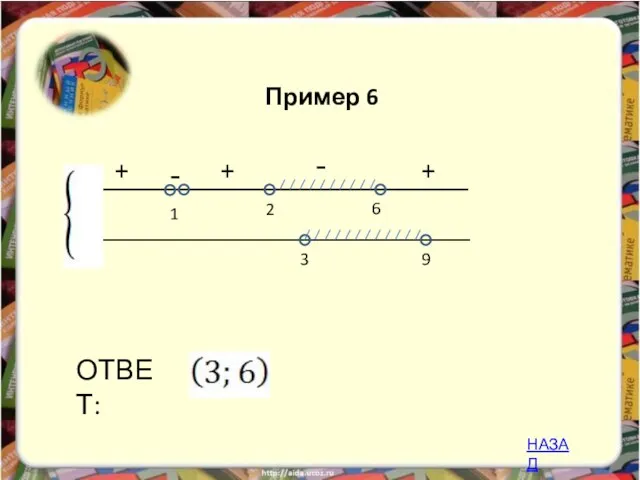
6
2
ОТВЕТ:
1
3
9
+
-
+
Пример 6
НАЗАД

+
-
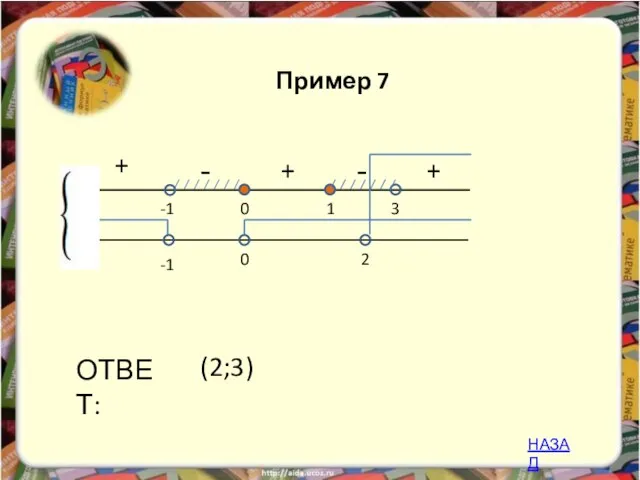
-1
3
1
ОТВЕТ:
0
-1
0
2
+
-
+
(2;3)
Пример 7
НАЗАД

-
+
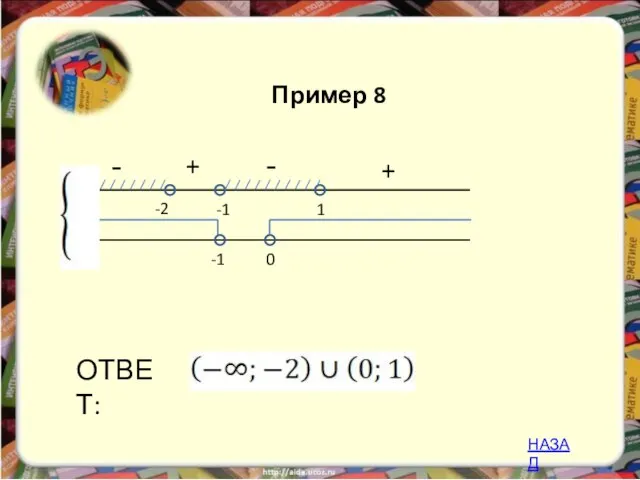
-2
1
ОТВЕТ:
-1
-1
0
+
-
Пример 8
НАЗАД

-
+
-3
1
0
ОТВЕТ:
-1
-1/2
4
+
+
-
Пример 9
НАЗАД

-
+
3
ОТВЕТ:
1
1
2
+
+
-
Пример 10
НАЗАД

3/2
ОТВЕТ:
0
5/4
Пример 11