Темы: График квадратичной функции. Неравенства с одной переменной.

Квадратичная функция и ее график.
Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая переменная, a,b,c -некоторые числа, причём a ≠ 0.
Графиком квадратичной функции является парабола
Алгоритм построения параболы.
f(x) = ax² + bx + c
Направление ветвей
Вершина ( x = -b ∕ 2a; y = f(x ). )
Ось симметрии.
Таблица значений
Построение графика

Пример построения графика квадратичной функции.
F(x)= 2x² + 8x +2
1) Ветви 2) х = -b ∕ 2a= -8∕ 2•2= -2
y = f(x )= 2•(-2)² + 8•(-2)+2= -6
O (-2;-6)
3)
4)
у
х
-2
-6

Неравенства второй степени с одной переменной.
Неравенства вида ax²+bx+c>0 и ax²+bx+c<0, где х – переменная, a,b,c – некоторые числа, причём а ≠ 0, называют неравенствами второй степени с одной переменной.
Алгоритм решения квадратного неравенства.
1) Вводим функцию (у…..),
2) Находим нули функции (у=0),
3) Определяем направление ветвей,
4) Делаем схематический рисунок ,
5) Выбираем ответ.

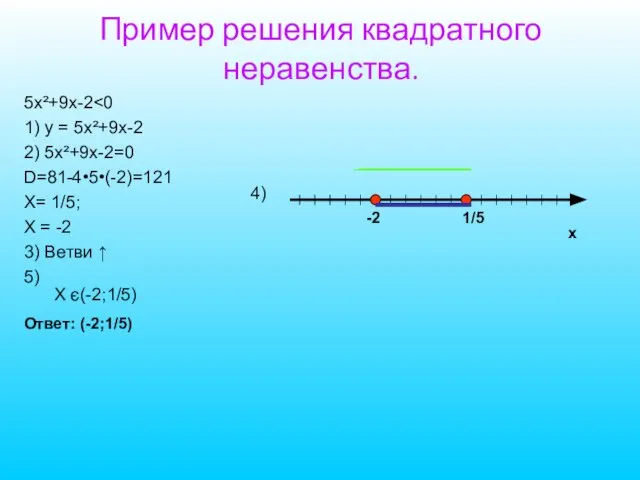
Пример решения квадратного неравенства.
5х²+9х-2<0
1) у = 5х²+9х-2
2) 5х²+9х-2=0
D=81-4•5•(-2)=121
Х= 1/5;
Х = -2
3) Ветви ↑
5)
х
-2
4)
Х є(-2;1/5)
1/5
Ответ: (-2;1/5)