Применения матриц в экономике

Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m  n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аi j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:

МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО
СКЛАДЫВАТЬ И ВЫЧИТАТЬ

ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ
МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B

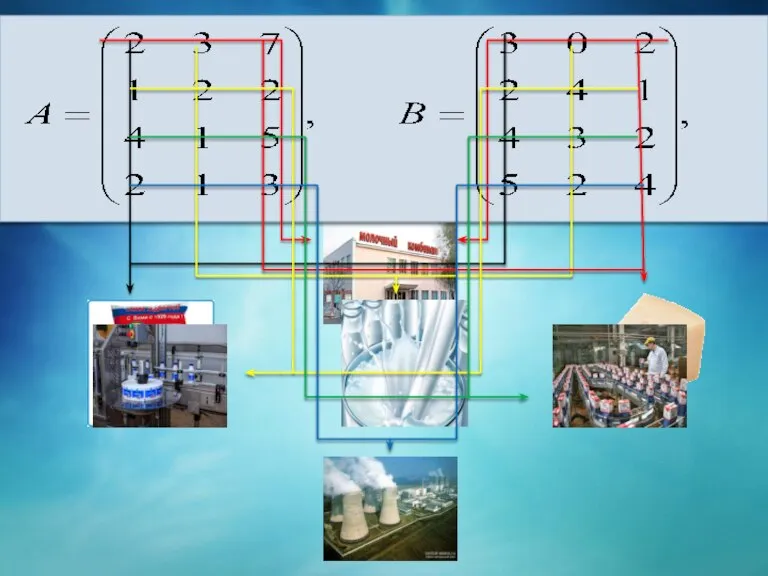
Понятие матрицы часто используется в практической деятельности.
Например, данные о выпуске продукции нескольких видов в каждом квартале года или нормы затрат нескольких видов ресурсов на производство продукции нескольких типов и т.д. удобно записать в виде матриц.

В некоторой отросли m заводов выпускают n типов продукции. Матрица Amxn- задает объемы продукции на каждом заводе в первом квартале, матрица Bmxn-соответственно во втором;
(aij, bij) - объемы продукции j–го типа на i–м заводе
в 1-м и 2-м кварталах соответственно:

Найти:
а) объемы продукции;
б) прирост объемов производства во втором квартале по сравнению с первым по видам продукции и заводам;
в) стоимостное выражение выпущенной продукции за полгода (в долларах), если –курс доллара по отношению к самону.

а) Объемы продукции за полугодие определяются суммой матриц А и В, т.е.
С=А+В =
где сij=аij+bij–объем продукции j–го типа, произведенный за полугодие i–м заводом

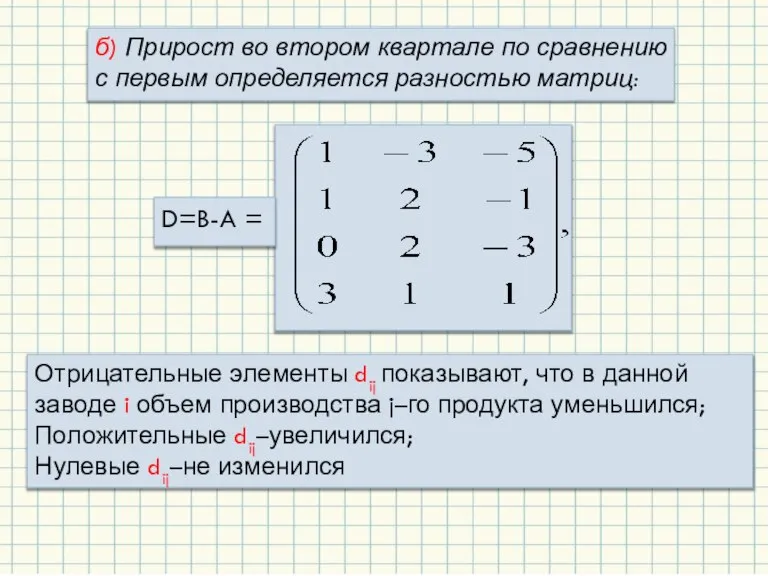
б) Прирост во втором квартале по сравнению с первым определяется разностью матриц:
D=B-A =
Отрицательные элементы dij показывают, что в данной заводе i объем производства j–го продукта уменьшился;
Положительные dij–увеличился;
Нулевые dij–не изменился

в) Произведение дает выражение стоимости объемов производства за квартал в долларах по каждому заводу и каждому предприятию:

Предприятие производит n типов продукции, объемы выпуска заданы матрицей A1xn. Цена реализации единицы i-го типа продукции в j-м регионе задана матрицей Bnxk, где k-число регионов, в которых реализуется продукция
Найти C-матрицу выручки по регионам.

A1x3 =(100, 200, 100);

Выручка определяется матрицей C1xk = A1xn x Bnxn
причем – это выручка
предприятия в j–м регионе: