Содержание
- 2. QUELQUES REMARQUES PRELIMINAIRES Un mouvement harmonique simple existe lorsqu’une force de rappel est appliquée au système.
- 3. Il peut se produire un phénomène de résonance dans le cas où le système est entraîné
- 4. TERMINOLOGIE Mouvement périodique Mouvement ou évènement qui se répète à des intervalles réguliers T période du
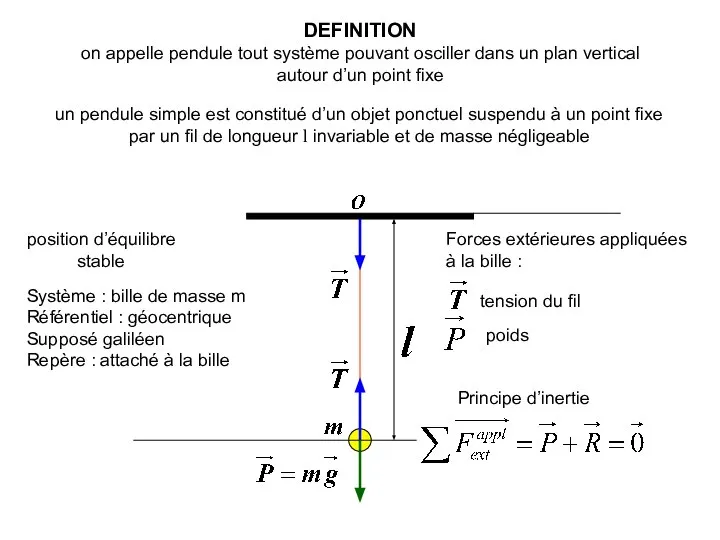
- 5. DEFINITION on appelle pendule tout système pouvant osciller dans un plan vertical autour d’un point fixe
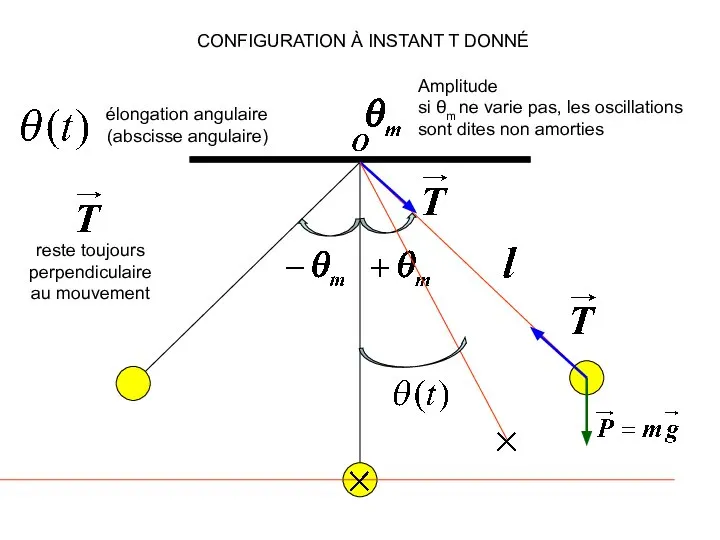
- 6. élongation angulaire (abscisse angulaire) Amplitude si θm ne varie pas, les oscillations sont dites non amorties
- 7. CONFIGURATION À INSTANT T DONNÉ Projections sur les axes du repère
- 8. projection sur les deux axes perpendiculaires Ox, tangente au mouvement Oy, axe radial POSITION D’ÉQUILIBRE STATIQUE
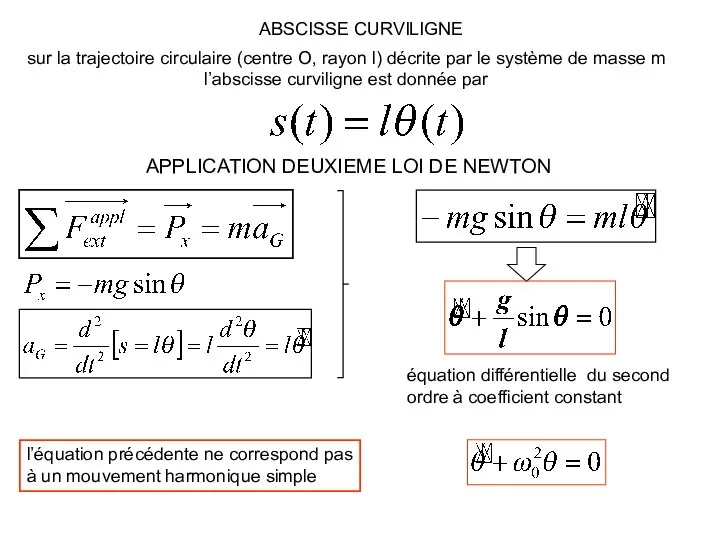
- 9. ABSCISSE CURVILIGNE sur la trajectoire circulaire (centre O, rayon l) décrite par le système de masse
- 10. HYPOTHESE DES PETITES OSCILLATIONS ISOCHRONISME équation du mouvement dans ces conditions on retrouve l’écriture générale du
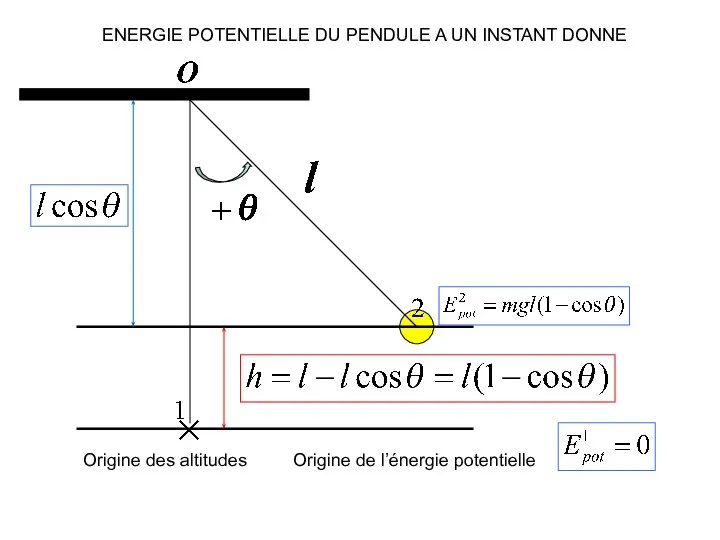
- 11. ENERGIE POTENTIELLE DU PENDULE A UN INSTANT DONNE Origine des altitudes Origine de l’énergie potentielle
- 12. ENERGIE CINETIQUE DU PENDULE A UN INSTANT DONNE Rappel de l’abscisse curviligne : VITESSE
- 13. ENERGIE MECANIQUE DU PENDULE A UN INSTANT DONNE Le système est isolé, pas de frottements, il
- 14. VARIATION DE L’ÉNERGIE MÉCANIQUE EN FONCTION DU TEMPS L’énergie mécanique est constante donc : On aboutit
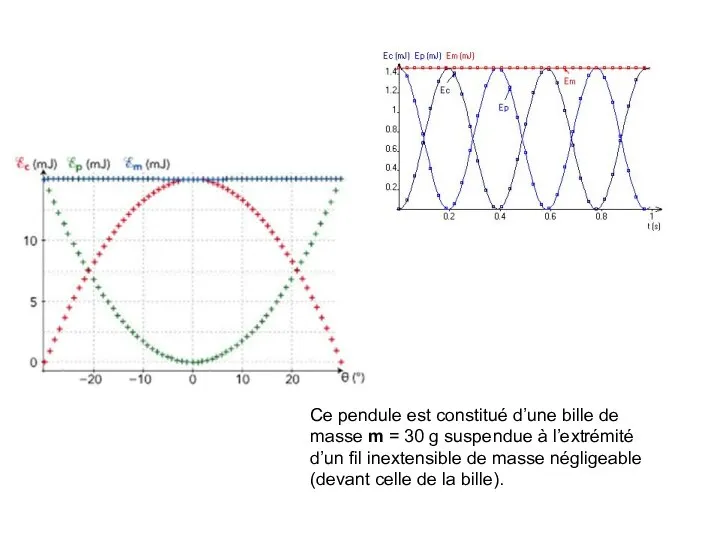
- 15. Ce pendule est constitué d’une bille de masse m = 30 g suspendue à l’extrémité d’un
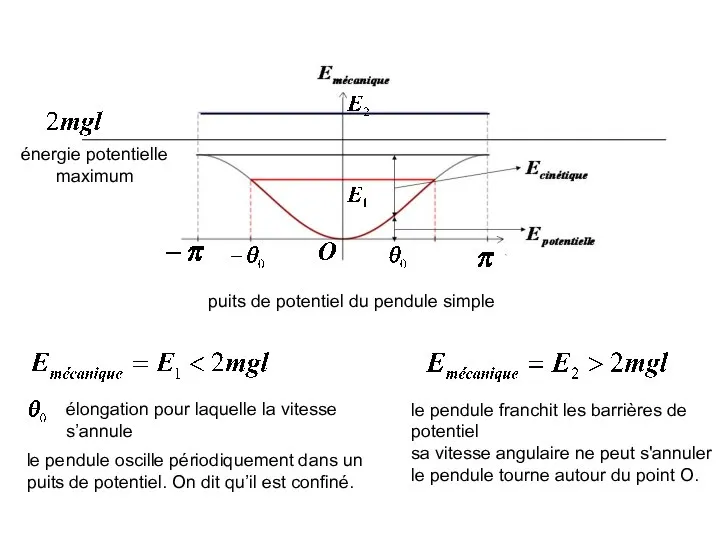
- 16. énergie potentielle maximum puits de potentiel du pendule simple le pendule oscille périodiquement dans un puits
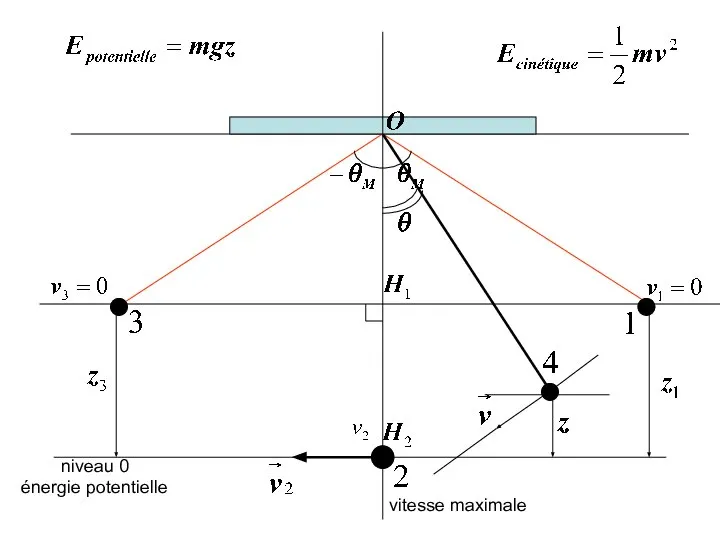
- 17. niveau 0 énergie potentielle vitesse maximale
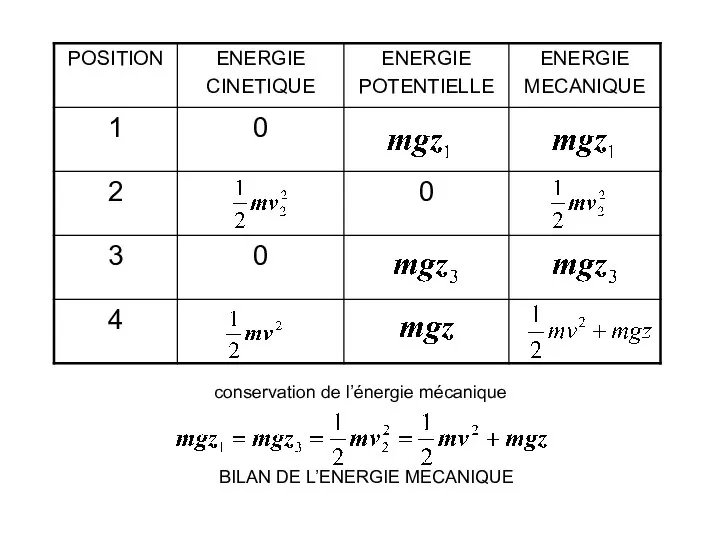
- 18. conservation de l’énergie mécanique BILAN DE L’ENERGIE MECANIQUE
- 20. Скачать презентацию









 Транзистор. Виды транзисторов
Транзистор. Виды транзисторов Газовые законы
Газовые законы Двоступеневі гіроскопи
Двоступеневі гіроскопи Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Изделие и техническая информация о нем
Изделие и техническая информация о нем Презентация по физике "Его Величество - Электричество" -
Презентация по физике "Его Величество - Электричество" -  Вклад Д.И. Менделеева в развитие метрологии
Вклад Д.И. Менделеева в развитие метрологии The atom
The atom Общие сведения о системе пуска
Общие сведения о системе пуска Плотность вещества
Плотность вещества Единая система допусков и посадок деталей и узлов машин, принципы её построения
Единая система допусков и посадок деталей и узлов машин, принципы её построения Источники электрического тока
Источники электрического тока Реактивное движение
Реактивное движение Электроизмерительные приборы, закон Ампера
Электроизмерительные приборы, закон Ампера Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели
Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели Презентация на тему Плавание тел
Презентация на тему Плавание тел  Сила Лоренца
Сила Лоренца Игровая встреча. Великие физики
Игровая встреча. Великие физики Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9)
Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9) УФ-спектроскопия. Часть 1
УФ-спектроскопия. Часть 1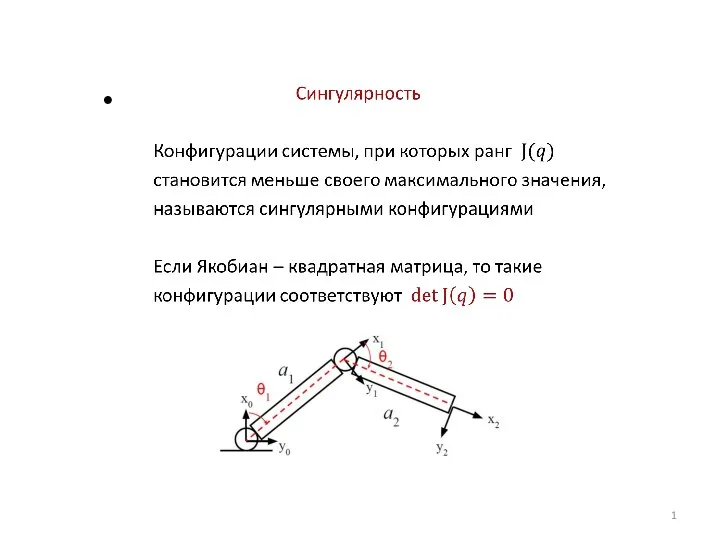 Сингулярность. Сингулярные конфигурации
Сингулярность. Сингулярные конфигурации Техосмотр
Техосмотр Презентация на тему Солнце (11 класс)
Презентация на тему Солнце (11 класс)  Задачи по технической механике. Сложение ускорений
Задачи по технической механике. Сложение ускорений Постоянные магниты. Магнитное поле Земли
Постоянные магниты. Магнитное поле Земли Оценка прочности плоской фермы при нагреве
Оценка прочности плоской фермы при нагреве Презентация на тему Влияние радиоактивного излучения на живые организмы
Презентация на тему Влияние радиоактивного излучения на живые организмы  Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв
Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв