Содержание
- 2. Десять решений одной задачи Ровно 35 лет назад автор этой статьи принял участие в своей первой
- 3. Все решения задач можно разделить на 2 группы 1. Решения, отравленные ядом цивилизации 2. Собирательные решения
- 4. РЕШЕНИЕ 1 РЕШЕНИЕ 2 РЕШЕНИЕ 3 РЕШЕНИЕ 4 РЕШЕНИЕ 5 РЕШЕНИЕ 6 РЕШЕНИЕ 7 РЕШЕНИЕ 8
- 5. Решение 1 C N P B D M Q A E Если из суммы углов пяти
- 6. Решение 2 Рассмотрим пятиугольник ABCDE. Сумма углов звезды равна сумме углов пятиугольника ABCDE минус сумма углов
- 7. Решение 3 Соединим точку O, взятую внутри звезды, с ее вершинами. Сумма углов звезды будет равна
- 8. C N P B D M Q R A E Решение 4 Соберем углы звезды в
- 9. C N P B D M Q R A E Решение 5 Рассмотрим треугольник ACE, углы
- 10. C N P B D M Q R A E Решение 6 Собираем углы звезды в
- 11. Решение 7 Собираем все углы в полный угол при вершине D. Угол D уже находится там.
- 12. Решение 8 Через точку R проведем прямую LT параллельную BD. Тогда D = LRA, B =
- 13. Решение 9 Это фантастическое решение принадлежит И.Ф. Шарыгину. Опишем вокруг звезды окружность и спроектируем углы на
- 14. Решение 10 Проведем окружность так, чтобы она пересекала стороны всех углов звезды. Воспользуемся теоремой: угол, вершина
- 16. Скачать презентацию













 Прямоугольник и его свойства
Прямоугольник и его свойства Умножение вектора на число
Умножение вектора на число Нахождение корней систем уравнений и уравнений с помощью графиков
Нахождение корней систем уравнений и уравнений с помощью графиков Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Геометрия. Как она возникла?
Геометрия. Как она возникла? Перпендикуляр и наклонная
Перпендикуляр и наклонная Многогранники вокруг нас
Многогранники вокруг нас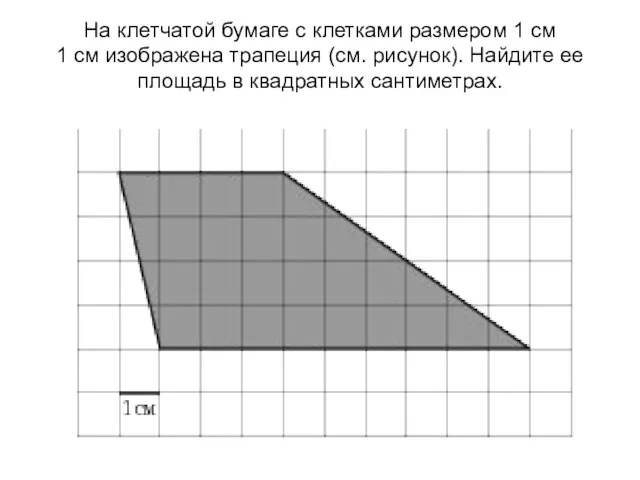 Площади фигур на клетке
Площади фигур на клетке Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Теорема синусов 9 класс
Теорема синусов 9 класс Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы Чудеса симметрии
Чудеса симметрии Тетраэдр и параллепипед
Тетраэдр и параллепипед ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Касательная к окружности 7 класс
Касательная к окружности 7 класс Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Площади
Площади Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Прямоугольный треугольник и его свойства
Прямоугольный треугольник и его свойства Окружности
Окружности Угол между плоскостями
Угол между плоскостями Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Окружность и круг
Окружность и круг Применение параллелограмма
Применение параллелограмма Многообразие многоугольников
Многообразие многоугольников Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Построение диаграмм и графиков
Построение диаграмм и графиков