«Чтение графиков. ЕГЭ» ЮВАО

Цель
Создать презентацию, которая поможет учащимся правильно определять по готовым графикам ответы к заданиям ЕГЭ.

Функция задана графиком. Укажите область определения этой функции.
1) [-4;2]
2) [-2;6]
3) [-3;4]
4) (-2;6)
Область определения функции
Все значения, которые принимает независимая переменная х, при которых функция имеет смысл, образуют область определения функции

На рисунке изображен график функции, заданной на промежутке [- 5;6]. Укажите множество значений этой функции
1) [-5;6)
2) [-2;4]
3) (-3;4]
4) (-3;2]
Область значений функции
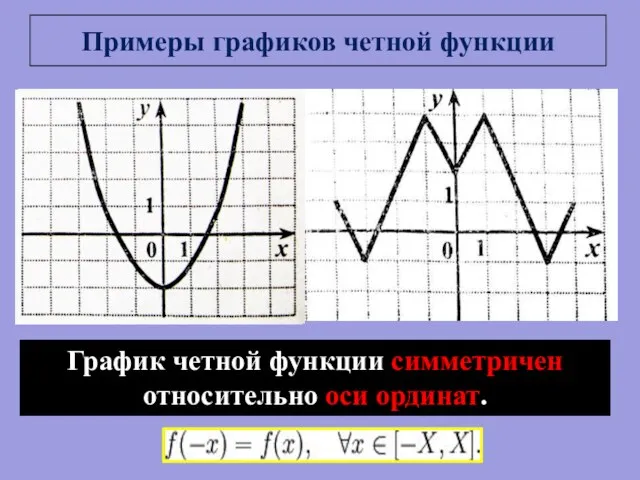
Множество, состоящее из всех чисел f(x), таких, что х принадлежит области определения функции f,называют областью значений функции.

Примеры графиков четной функции
График четной функции симметричен относительно оси ординат.

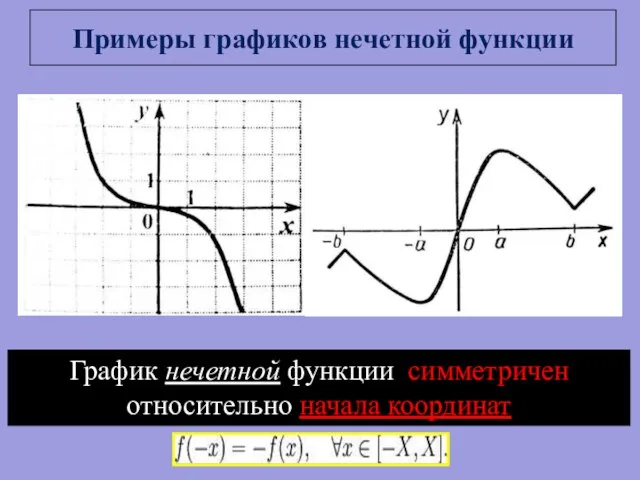
Примеры графиков нечетной функции
График нечетной функции симметричен относительно начала координат

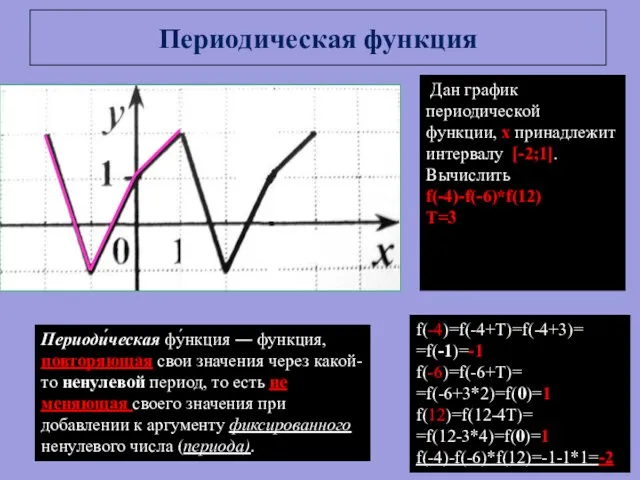
Периодическая функция
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).
Дан график периодической функции, x принадлежит интервалу [-2;1]. Вычислить
f(-4)-f(-6)*f(12)
T=3
f(-4)=f(-4+T)=f(-4+3)=
=f(-1)=-1
f(-6)=f(-6+T)=
=f(-6+3*2)=f(0)=1
f(12)=f(12-4T)=
=f(12-3*4)=f(0)=1
f(-4)-f(-6)*f(12)=-1-1*1=-2

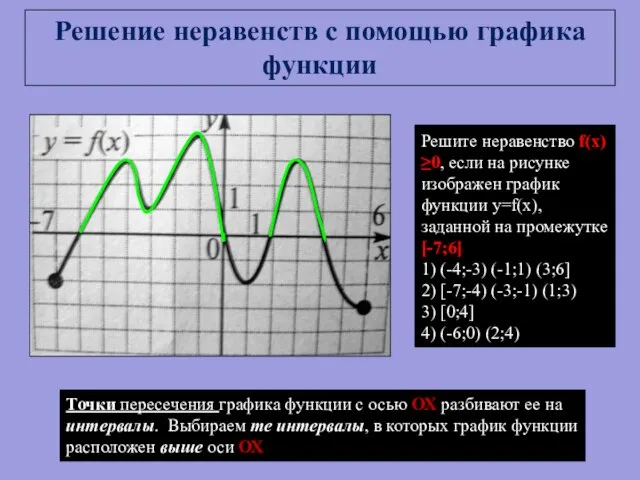
Решите неравенство f(x)≥0, если на рисунке изображен график функции y=f(x), заданной на промежутке
[-7;6]
1) (-4;-3) (-1;1) (3;6]
2) [-7;-4) (-3;-1) (1;3)
3) [0;4]
4) (-6;0) (2;4)
Решение неравенств с помощью графика функции
Точки пересечения графика функции с осью ОХ разбивают ее на интервалы. Выбираем те интервалы, в которых график функции расположен выше оси ОХ

На рисунке изображен график функции y=f(x), заданной на отрезке [-4;7]. Укажите все значения Х, для которых выполняется неравенство f(x)≥-1.
[-0,5;3]
[-0,5;3] U [3;7]
[-4;0,5] U [3;7]
[-4;0,5]
1. Проводим прямую у=-1, она пересекает график в двух точках.
2. Опускаем перпендикуляры из этих точек на ось ОХ. Они разбивают ось ОХ на три промежутка. 3. Выбираем промежуток, где график функции f(x) выше прямой у=-1.
Решение неравенств с помощью графика функции

На рисунке изображены графики функций y=f(x),и y=g(x), заданных на промежутке [-3;6]. Укажите все значения Х, для которых выполняется неравенство f(x)≤g(x)
[-1;2]
[-2;3]
[-3;-2] U [3;6] +
[-3;-1] U [3;4]
Сравнение значений функций
1. Находим точки пересечения графиков. 2. Опускаем перпендикуляры на ось ОХ. Они разбивают ось ОХ на три промежутка. 3. Выбираем промежуток, где точки графика функции f(x) ниже точек графика функции g(x).

На одном из рисунков изображен график функции, возрастающей на отрезке [0;2]. на другом - убывающей на отрезке [-2;0]. Укажите эти рисунки.
График возрастающей и убывающей функций

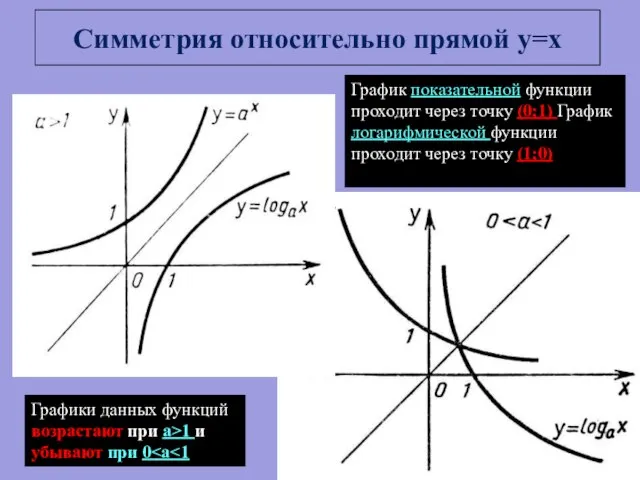
Симметрия относительно прямой y=x
Графики данных функций возрастают при а>1 и убывают при 0<а<1
График показательной функции проходит через точку (0;1) График логарифмической функции проходит через точку (1;0)

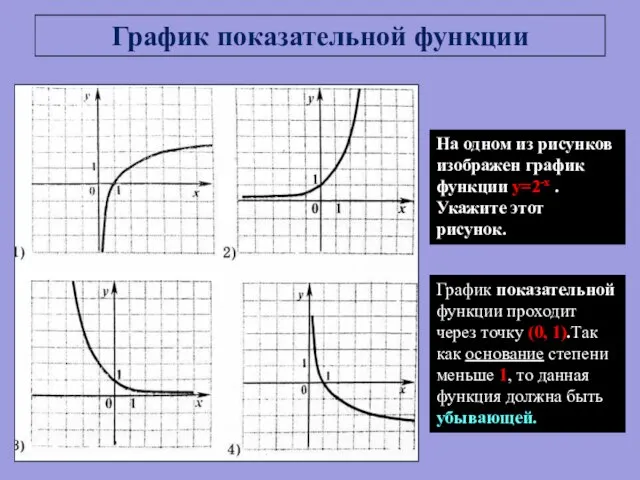
На одном из рисунков изображен график функции y=2-x .
Укажите этот рисунок.
График показательной функции
График показательной функции проходит через точку (0, 1).Так как основание степени меньше 1, то данная функция должна быть убывающей.

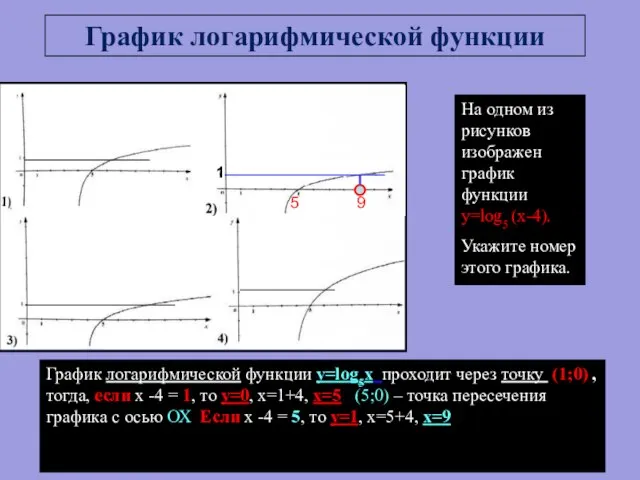
На одном из рисунков изображен график функции y=log5 (x-4).
Укажите номер этого графика.
График логарифмической функции y=log5x проходит через точку (1;0) , тогда, если х -4 = 1, то у=0, х=1+4, х=5. (5;0) – точка пересечения графика с осью ОХ Если х -4 = 5, то у=1, х=5+4, х=9,
График логарифмической функции
9
5
1

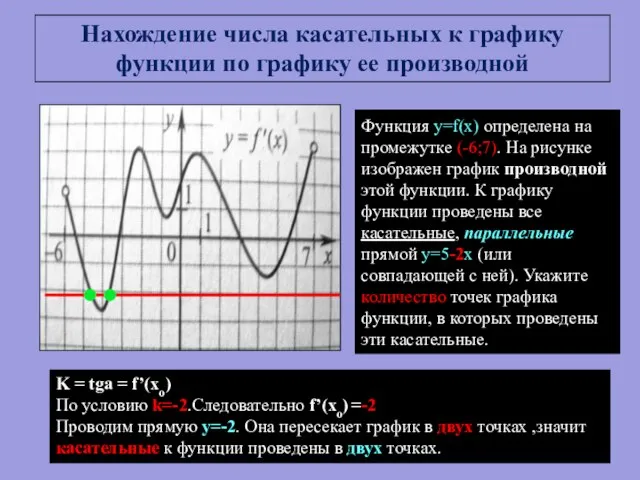
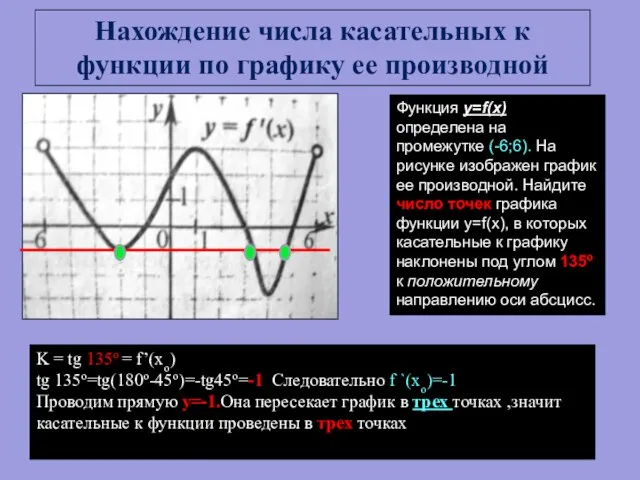
Функция y=f(x) определена на промежутке (-6;7). На рисунке изображен график производной этой функции. К графику функции проведены все касательные, параллельные прямой y=5-2x (или совпадающей с ней). Укажите количество точек графика функции, в которых проведены эти касательные.
K = tga = f’(xo)
По условию k=-2.Следовательно f’(xo) =-2
Проводим прямую у=-2. Она пересекает график в двух точках ,значит касательные к функции проведены в двух точках.
Нахождение числа касательных к графику функции по графику ее производной

Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику параллельны оси абсцисс или совпадают с ней.
Угловой коэффициент прямых, параллельных оси абсцисс или совпадающих с ней равен нулю. Следовательно К=tg a = f `(xo)=0
Ось ОХ пересекает данный график в четырех точках.
Нахождение числа касательных к функции по графику ее производной

Функция y=f(x) определена на промежутке (-6;6). На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику наклонены под углом 135о к положительному направлению оси абсцисс.
K = tg 135o = f’(xo)
tg 135o=tg(180о-45o)=-tg45o=-1 Следовательно f `(xo)=-1
Проводим прямую у=-1.Она пересекает график в трех точках ,значит касательные к функции проведены в трех точках
.
Нахождение числа касательных к функции по графику ее производной

Функция y=f(x) определена на промежутке [-2;6]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьший угловой коэффициент
k=tg a=f’(xo)
Наименьшее значение у=-3 производная функции принимает в точке х=2. Следовательно, касательная к графику имеет наименьший угловой коэффициент в точке х=2
Нахождение углового коэффициента касательной
по графику производной функции
-3
2

Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наибольший угловой коэффициент.
k=tg a=f’(xo)
Наибольшее значение у=3 производная функции принимает в точке х=-5.
Следовательно касательная к графику имеет наибольший угловой коэффициент в точке х=-5
Нахождение углового коэффициента касательной
по графику производной функции
3
-5

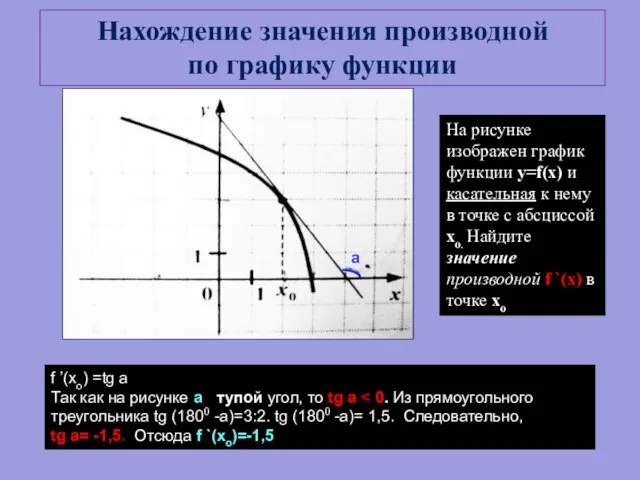
На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой хо. Найдите значение производной f `(x) в точке хо
f ’(xo) =tg a
Так как на рисунке а - тупой угол, то tg a < 0. Из прямоугольного треугольника tg (1800 -a)=3:2. tg (1800 -a)= 1,5. Следовательно,
tg a= -1,5. Отсюда f `(xo)=-1,5
Нахождение значения производной
по графику функции
а

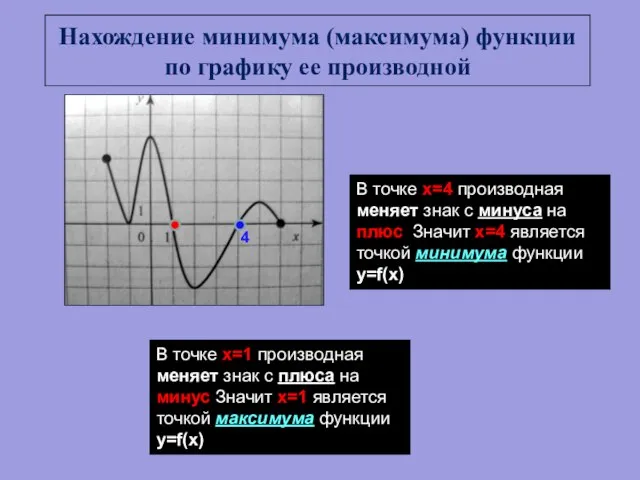
Нахождение минимума (максимума) функции по графику ее производной
В точке х=4 производная меняет знак с минуса на плюс. Значит х=4 является точкой минимума функции y=f(x)
4
В точке х=1 производная меняет знак с плюса на. минус Значит х=1 является точкой максимума функции y=f(x))

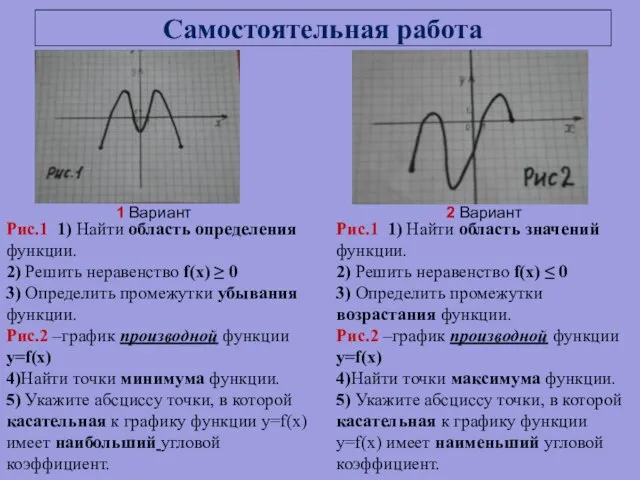
Самостоятельная работа
Рис.1 1) Найти область определения функции.
2) Решить неравенство f(x) ≥ 0
3) Определить промежутки убывания функции.
Рис.2 –график производной функции y=f(x)
4)Найти точки минимума функции.
5) Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наибольший угловой коэффициент.
Рис.1 1) Найти область значений функции.
2) Решить неравенство f(x) ≤ 0
3) Определить промежутки возрастания функции.
Рис.2 –график производной функции y=f(x)
4)Найти точки максимума функции.
5) Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьший угловой коэффициент.
1 Вариант
2 Вариант

ЛИТЕРАТУРА
Математика ЕГЭ 2008.
Т. А. Корешкова, Ю. А.Глазков,
В. В.Мирошин, Н. В.Шевелева
Математика ЕГЭ 2009.
В. И. Ишина, Л.О. Денищева и др.
3. Алгебра и начала анализа
А. Н. Колмогоров.