Содержание
- 2. Определение Решить треугольник-это по трем элементам треугольника найти остальные три элемента.
- 3. НАЙДЕНЫ СЛЕДУЮЩИЕ ЗАДАЧИ ПОДВУМ УГЛАМ И СТОРОНЕ ПО ДВУМ СТОРОНАМ И УГЛУ ПО ТРЕМ СТОРОНАМ ПО
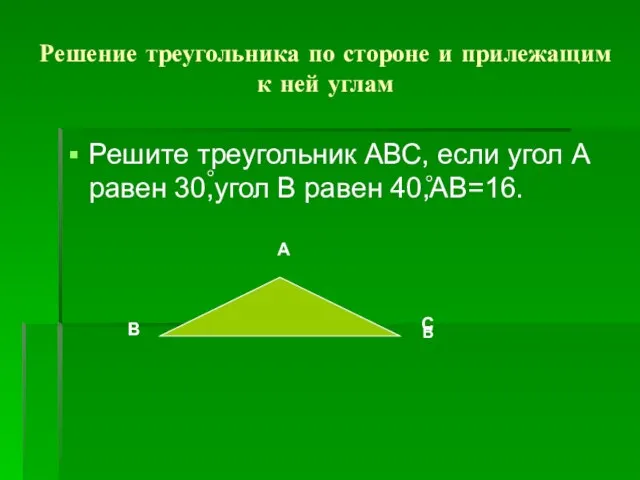
- 4. Решение треугольника по стороне и прилежащим к ней углам Решите треугольник АВС, если угол А равен
- 5. Нам потребуется теорема синусов
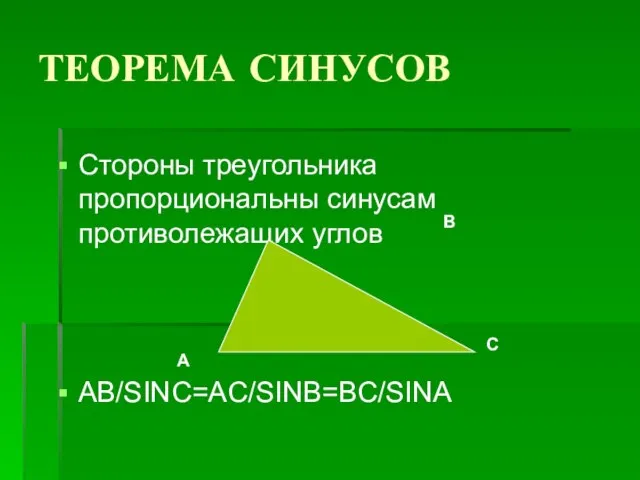
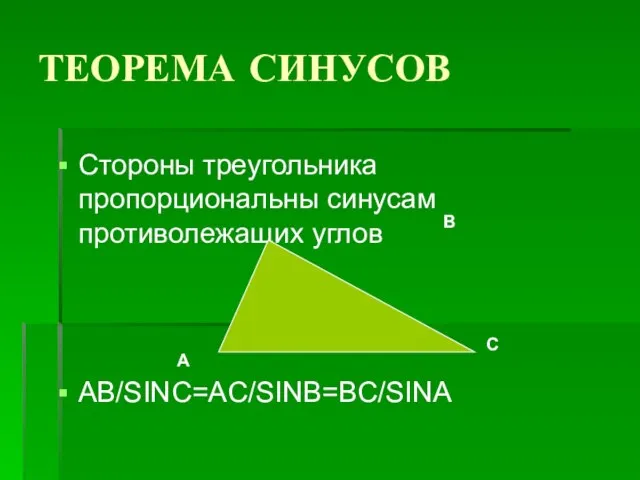
- 6. ТЕОРЕМА СИНУСОВ Стороны треугольника пропорциональны синусам противолежащих углов AB/SINC=AC/SINB=BC/SINA А В С
- 7. Решение треугольника по стороне и прилежащим к ней углам ABС С=180-(30+40)=(180-70)=110 A=30 По теореме синусов Дано:
- 8. Реши сам Дано: ABC BC=0,75 B=40 C=25 Найти: АС-?
- 9. Ответ 41,2 ОБРАТНО
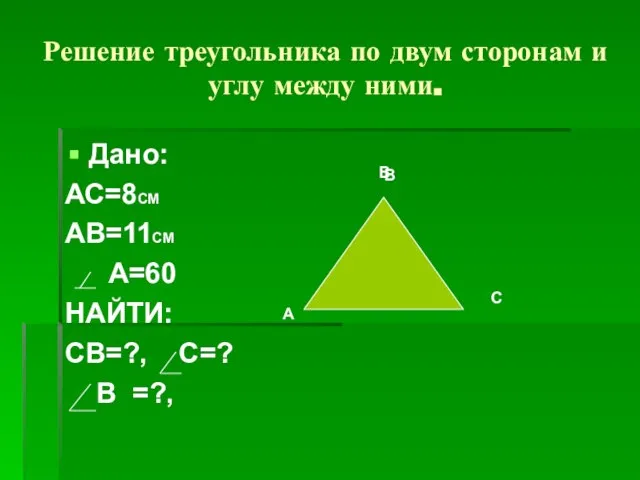
- 10. Решение треугольника по двум сторонам и углу между ними. Решите треугольник , если АВ=6см,ВС=8см,СА=10см А В
- 11. Нам потребуется теорема синусов и терема косинусов
- 12. Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон
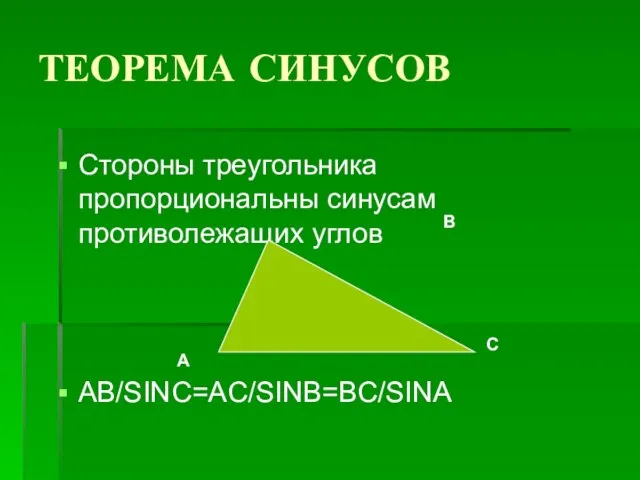
- 13. ТЕОРЕМА СИНУСОВ Стороны треугольника пропорциональны синусам противолежащих углов AB/SINC=AC/SINB=BC/SINA А В С
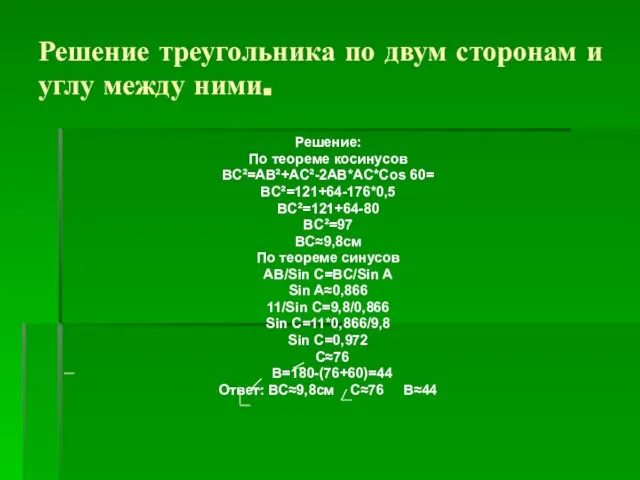
- 14. Решение треугольника по двум сторонам и углу между ними. Дано: АС=8СМ АВ=11СМ А=60 НАЙТИ: СВ=?, С=?
- 15. Решение треугольника по двум сторонам и углу между ними. Решение: По теореме косинусов ВС²=AB²+AC²-2AB*AC*Cos 60= BC²=121+64-176*0,5
- 16. Реши сам Дано: АВМ АВ=5 АМ=8 ВАМ=60 Найти: ВМ-? Sin ABM-?
- 17. Ответ ВМ=7см Sin ABM=4√3/7 обратно
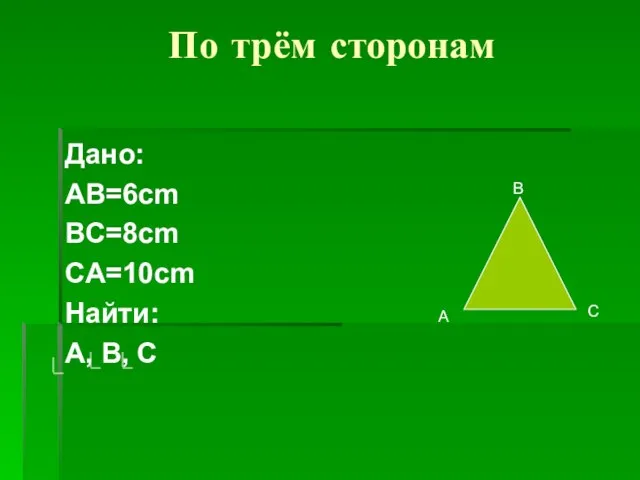
- 18. По трём сторонам Дано: AB=6cm BC=8cm CA=10cm Найти: A, B, C В А С
- 19. Нам потребуется теорема синусов и теорема косинусов
- 20. ТЕОРЕМА СИНУСОВ Стороны треугольника пропорциональны синусам противолежащих углов AB/SINC=AC/SINB=BC/SINA А В С
- 21. Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон
- 22. ПО ТРЕМ СТОРОНАМ Дано: Решение: АВ=6см ВС=8см СА=10см По теореме косинусов АВ²=ВС²+СА²-2*ВС*СА*Соs C Сos C=(BC²+CA²-AB²)/(2BC*CA) Cos
- 23. Реши сам Стороны треугольника равны 9см,5√2см и √41см .Найдите величину угла, противолежащего стороне, равной √41
- 24. Ответ : 45 обратно
- 25. КОНЕЦ
- 27. Скачать презентацию

















 Что такое геометрия
Что такое геометрия ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Геометрия. Как она возникла?
Геометрия. Как она возникла?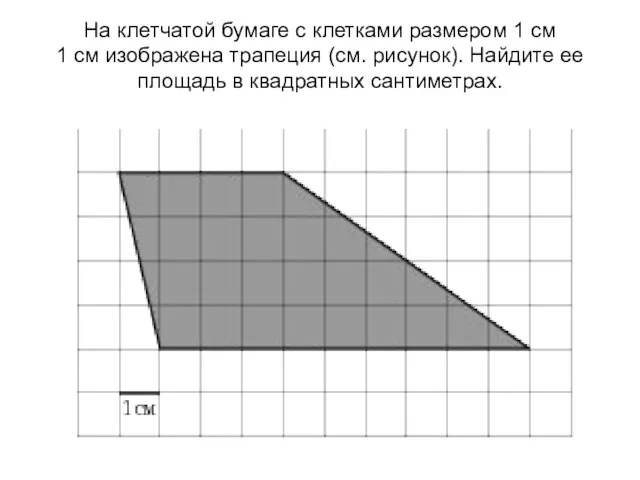 Площади фигур на клетке
Площади фигур на клетке Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Стереометрия в образах
Стереометрия в образах Многообразие многоугольников
Многообразие многоугольников Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_
Площадь квадрата, прямоугольника, параллелограмма - презентация по Геометрии_ Бозон Хиддинса
Бозон Хиддинса Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Площадь многоугольника 8 класс
Площадь многоугольника 8 класс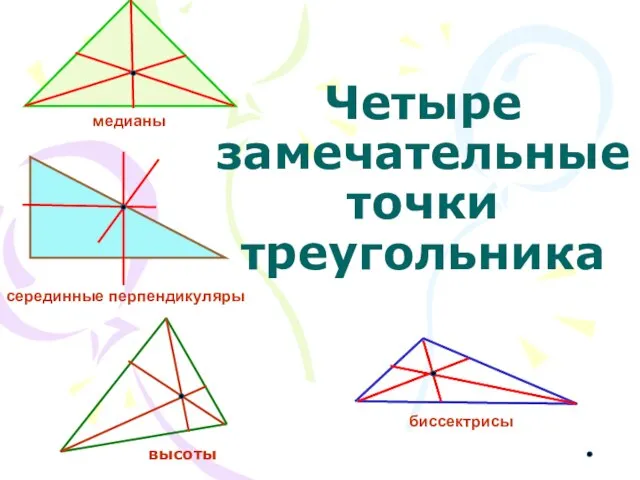 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника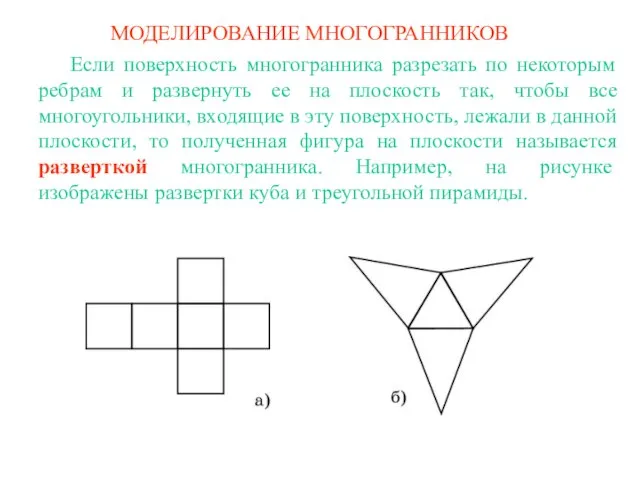 Моделирование многогранников
Моделирование многогранников Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Логарифм. Основные понятия
Логарифм. Основные понятия Расстояние от точки до прямой
Расстояние от точки до прямой Объём пирамиды
Объём пирамиды тренажёр по теме смежные и вертикальные углы
тренажёр по теме смежные и вертикальные углы Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Тригонометрические неравенства
Тригонометрические неравенства Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Параллелепипед
Параллелепипед