диагоналей.
Треугольники AOD и COB
равны. У них углы при вершине
О равны как вертикальные, а
OD= ОВ и ОА=ОС по условию
теоремы.
Значит, углы ОВС и ОDA равны,
А они являются внутренними накрест лежащими для прямых AD и BC и секущей BD.По признаку параллельности прямых прямые AD и BC параллельны. Так же доказывается параллельность прямых АВ и CD с помощью равенства
треугольников AOB и COD. Так КАК
ПРОТИВОЛЕЖАЩИЕ СТОРОНЫ ЧЕТЫРЁХУГОЛЬНИКА ПАРАЛЛЕЛЬНЫ, ТО ПО ОПРЕДЕЛЕНИЮ ЭТОТ ЧЕТЫРЁХУГОЛЬНИК- ПАРАЛЛЕЛОГРАММ. Теорема доказана.
A
B
D
C
O







 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием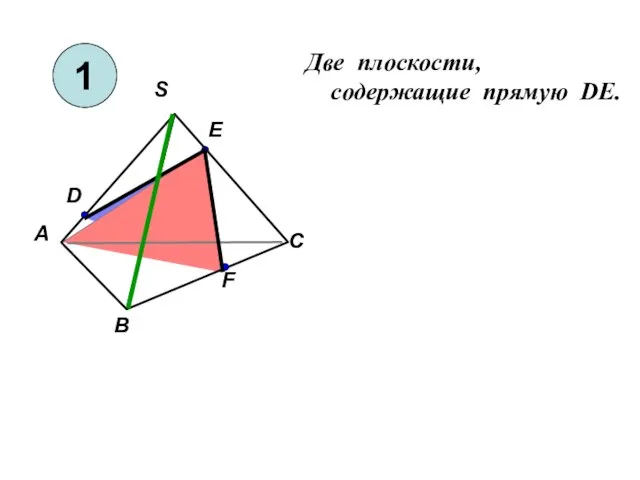 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия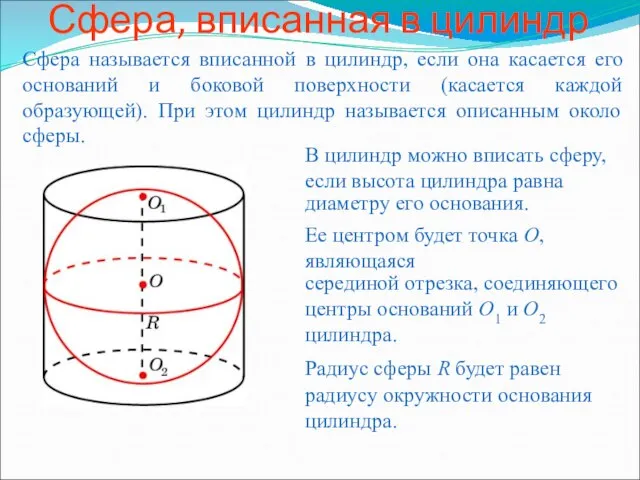 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика