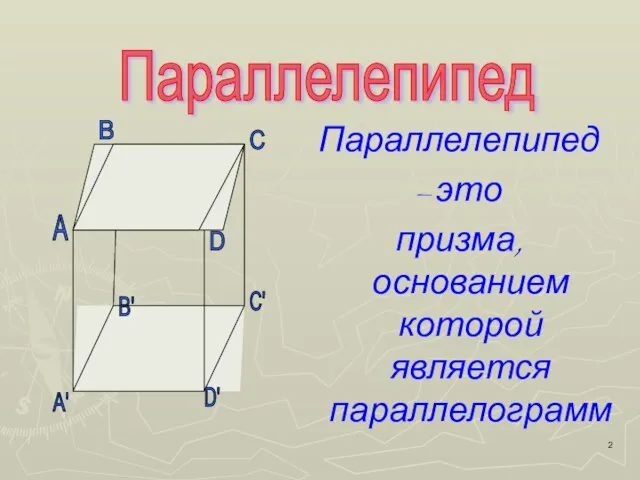
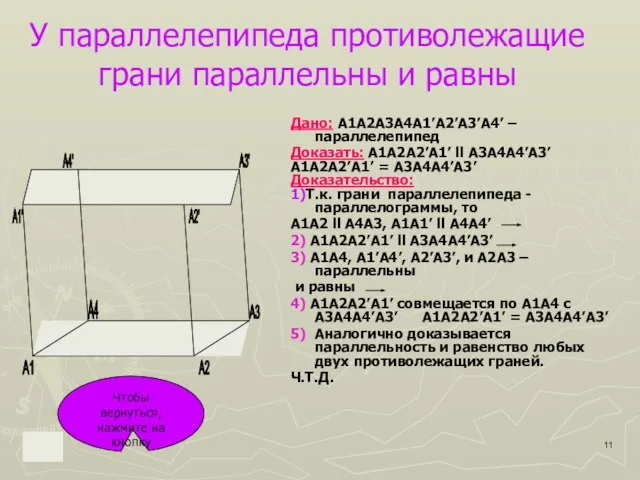
Параллелепипед

Параллелепипед
Параллелепипед
– это
призма, основанием которой является параллелограмм

Элементы параллелепипеда
Ребро основания
Нижнее основание
Верхнее основание
Боковая грань
Боковое ребро
Диагональ
Высота
Вершина
Противолежащие грани

Свойства параллелепипеда
У параллелепипеда все грани – параллелограммы
Основания параллелепипеда равны
Основания параллелепипеда лежат в параллельных плоскостях
Боковые рёбра параллельны и равны
Противолежащие грани параллельны и равны
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам

Виды параллелепипеда
Наклонный
Прямой
Боковые рёбра перпендикулярны основанию
прямоугольный
Куб
В основании лежит прямоугольник
Все грани - квадраты

Прямоугольный параллелепипед
Это прямой параллелепипед, у которого основанием является прямоугольник
У прямоугольного параллелепипеда все грани прямоугольники
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами.
У прямоугольного параллелепипеда три измерения
Квадрат диагонали равен сумме квадратов трех его измерений

Куб
Прямоугольный параллелепипед, у которого все рёбра равны
S=6a2
V=a3

Поверхность прямоугольного параллелепипеда
S
полн
2(ab+bc+ac)
=
Объём прямоугольного параллелепипеда
V = abc

Сечения параллелепипеда
Перпендикулярное
Диагональное

презентация закончена

У параллелепипеда противолежащие грани параллельны и равны
Дано: A1A2A3A4A1’A2’A3’A4’ – параллелепипед
Доказать: A1A2A2’A1’ ll А3А4A4’A3’
A1A2A2’A1’ = А3А4A4’A3’
Доказательство:
1)Т.к. грани параллелепипеда - параллелограммы, то
А1А2 ll A4A3, A1A1’ ll A4A4’
2) A1A2A2’A1’ ll А3А4A4’A3’
3) A1A4, A1’A4’, A2’A3’, и A2A3 – параллельны
и равны
4) A1A2A2’A1’ совмещается по А1А4 с А3А4А4’A3’ A1A2A2’A1’ = А3А4A4’A3’
5) Аналогично доказывается параллельность и равенство любых двух противолежащих граней.
Ч.Т.Д.
Чтобы вернуться, нажмите на кнопку

Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам
Дано: A1A2A3A4A1’A2’A3’A4’ – параллелепипед
А1А3’ и A4A2’ – диагонали, О – точка
пересечения диагоналей
Доказать: А1А3’ и A4A2’ пересекаются и точкой пересечения делятся пополам
Доказательство:
1) Т.к. А1А2А3А4 и А2А2’A3’A3
параллелограммы и А2А3 – общая, то А1А4 ll
А2’А3’ и лежат в одной плоскости (А1А4А3’А2’).
2) А1А4А3’А2’ пересекает плоскости противол. граней по
параллельным прямым А1А2 и А4А3’.
3) А1А4А3’А2’ – параллелограмм.
Диагонали параллелепипеда А1А3’ и A4A2’ –
диагонали этого параллелограмма. Они
пересекаются и точкой О делятся пополам.
4) Аналогично доказывается что А1А3’ и A2A4’, A1A3’ и A3A1’ пересекаются и точкой пересечения делятся пополам.
5) Отсюда, все четыре диагонали пересекаются в одной точке и делятся пополам.
Ч.Т.Д.
Чтобы вернуться, нажмите кнопку