Слайд 2Развитие геометрии, используемой
для описания природных процессов
Классическая
геометрия
Фрактальная геометрия
Слайд 3Фрактальные структуры в природе

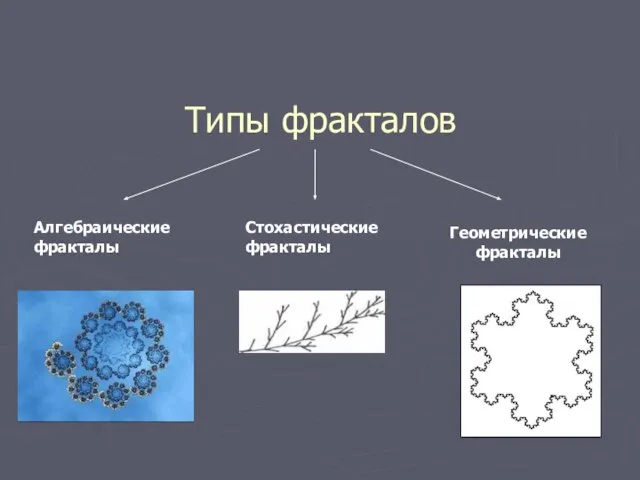
Слайд 4Типы фракталов
Геометрические
фракталы
Алгебраические
фракталы
Стохастические
фракталы
Слайд 5Алгебраические
фракталы
Самая крупная группа фракталов. Получают их с помощью нелинейных процессов в

n-мерных пространствах. Наиболее изучены двумерные процессы.
Слайд 6Стохастические
фракталы
Образуются в случае случайной перемены в итерационном процессе параметров фрактала. Двумерные

стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Слайд 7Геометрические фракталы
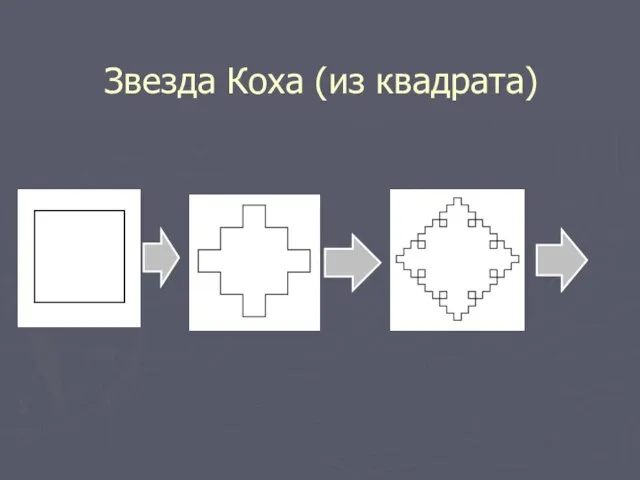
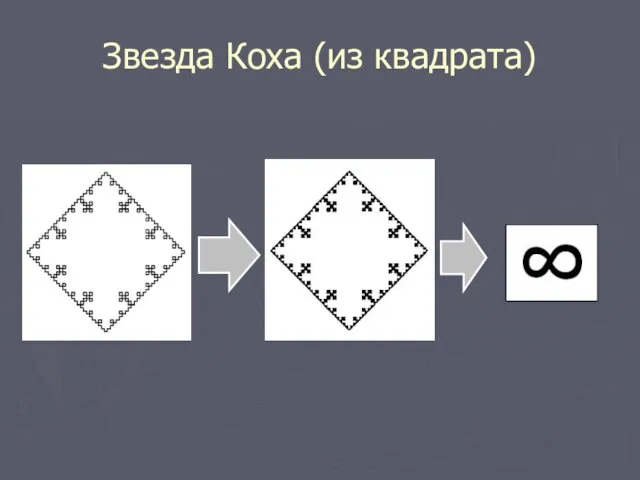
1). Звезда Коха
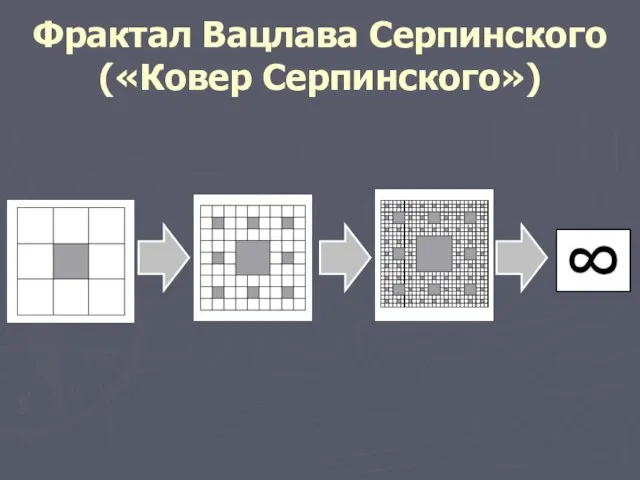
2). Фрактал Вацлава Серпинского («Ковер Серпинского»)
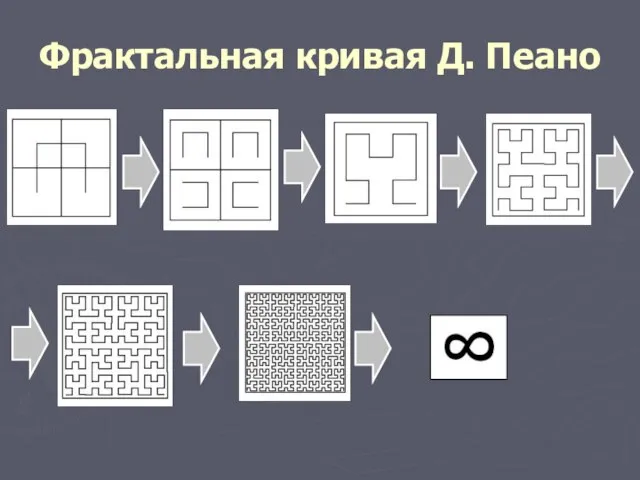
3). Фрактальная кривая

Д.Пеано
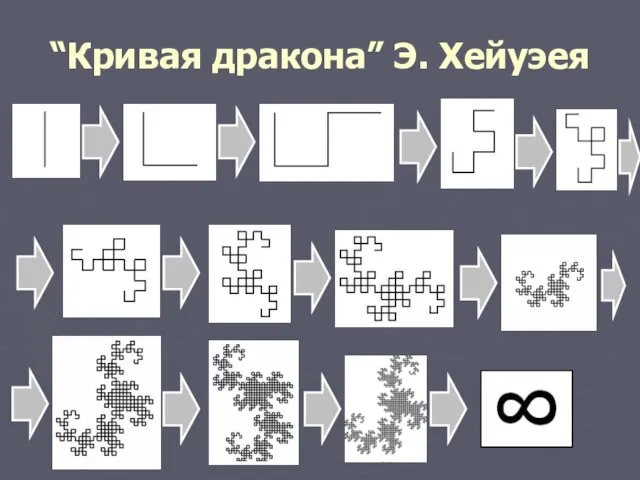
4). “Кривая дракона” Э. Хейуэея
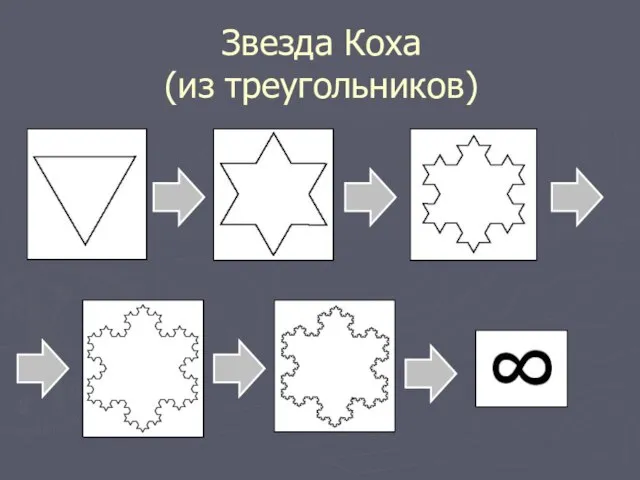
Слайд 8Звезда Коха
(из треугольников)
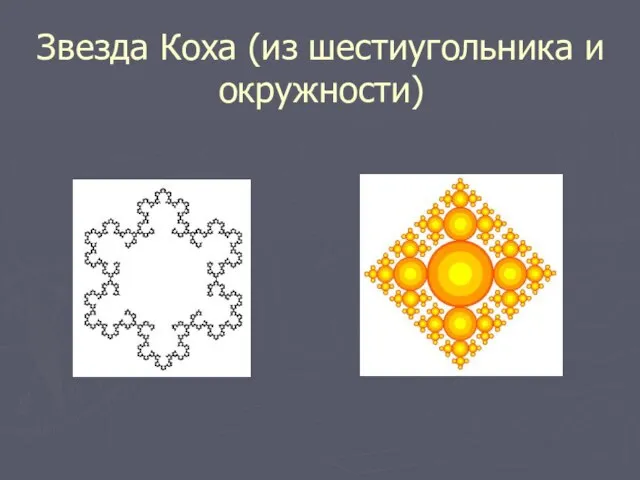
Слайд 11Звезда Коха (из шестиугольника и окружности)
Слайд 12Фрактал Вацлава Серпинского («Ковер Серпинского»)
Слайд 13Фрактал Вацлава Серпинского («Салфетка Серпинского»)
Получается из треугольника последовательным вырезанием серединных правильных треугольников











 Прямоугольник и его свойства
Прямоугольник и его свойства Умножение вектора на число
Умножение вектора на число Нахождение корней систем уравнений и уравнений с помощью графиков
Нахождение корней систем уравнений и уравнений с помощью графиков Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Геометрия. Как она возникла?
Геометрия. Как она возникла? Перпендикуляр и наклонная
Перпендикуляр и наклонная Многогранники вокруг нас
Многогранники вокруг нас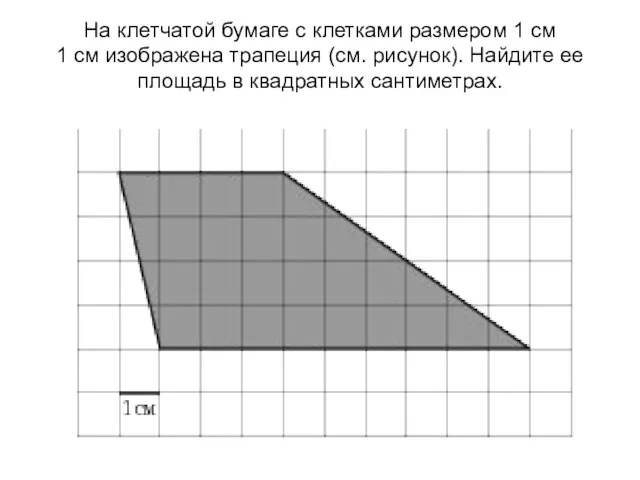 Площади фигур на клетке
Площади фигур на клетке Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Теорема синусов 9 класс
Теорема синусов 9 класс Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы Чудеса симметрии
Чудеса симметрии Тетраэдр и параллепипед
Тетраэдр и параллепипед ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Касательная к окружности 7 класс
Касательная к окружности 7 класс Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Площади
Площади Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Прямоугольный треугольник и его свойства
Прямоугольный треугольник и его свойства Окружности
Окружности Угол между плоскостями
Угол между плоскостями Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Окружность и круг
Окружность и круг Применение параллелограмма
Применение параллелограмма Многообразие многоугольников
Многообразие многоугольников Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Построение диаграмм и графиков
Построение диаграмм и графиков