Содержание
- 2. ЦЕЛИ УРОКА: закрепить теоретический материал по теме «Площадь»; совершенствовать навыки решения задач на вычисление площадей фигур.
- 3. Проверка домашнего задания №476, №478, №481, №474
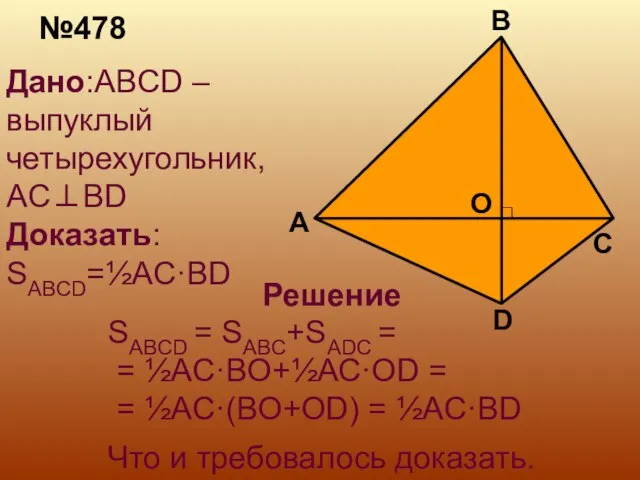
- 4. №478 Дано:ABCD –выпуклый четырехугольник, AC⊥BD Доказать: SABCD=½AC·BD Решение SABCD = SABC+SADC = = ½AC·BO+½AC·OD = =
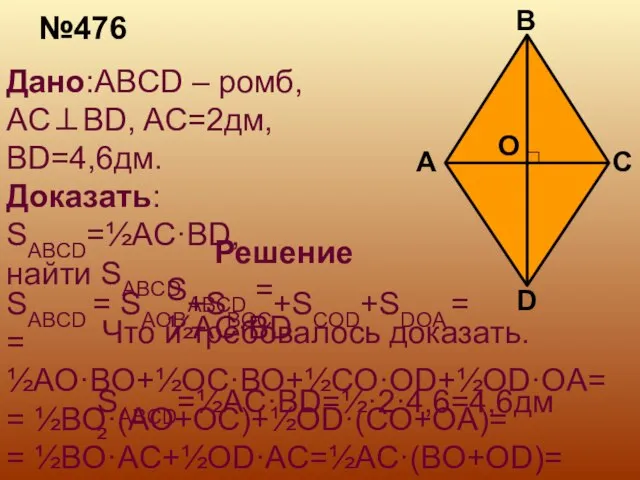
- 5. №476 Дано:ABCD – ромб, AC⊥BD, AC=2дм, BD=4,6дм. Доказать: SABCD=½AC·BD, найти SABCD Решение SABCD = SAOB+SBOC+SCOD+SDOA =
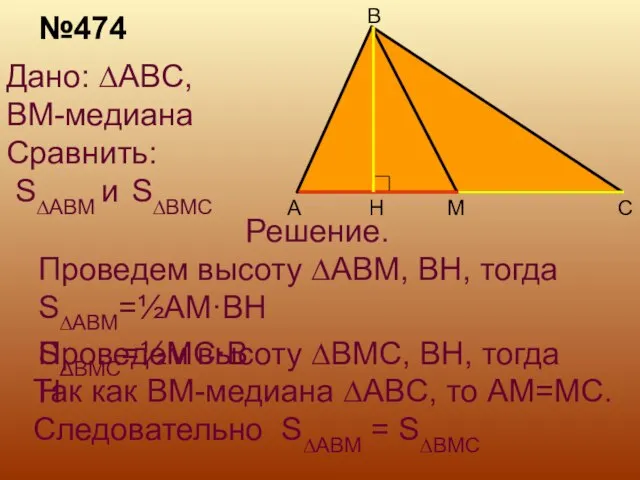
- 6. H Дано: ∆ABC, BM-медиана Сравнить: S∆ABM и S∆BMC Решение. Проведем высоту ∆ABM, BH, тогда S∆ABM=½AM·BH Так
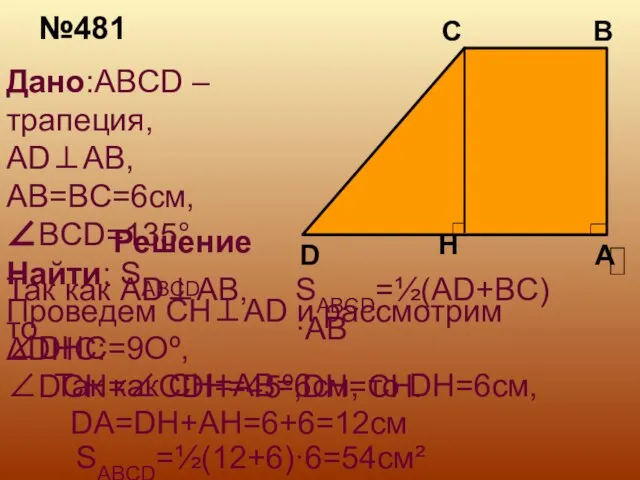
- 7. №481 Дано:ABCD –трапеция, AD⊥AB, AB=BC=6см, ∠BCD=135° Найти: SABCD Решение SABCD=½(AD+BC)·AB Так как AD⊥AB, то H Проведем
- 8. Решение задач на готовых чертежах
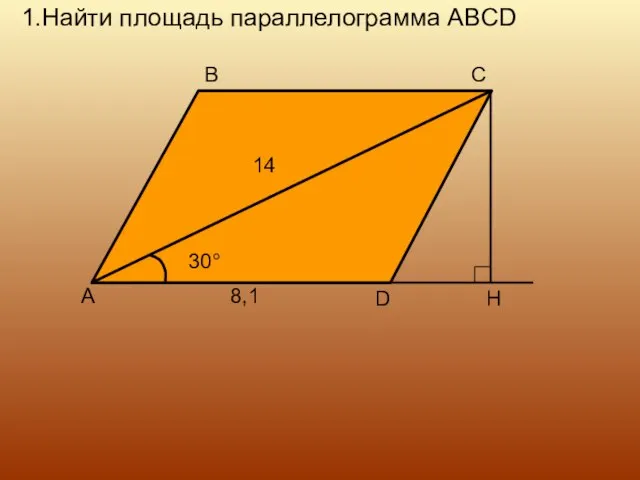
- 9. 1.Найти площадь параллелограмма ABCD H
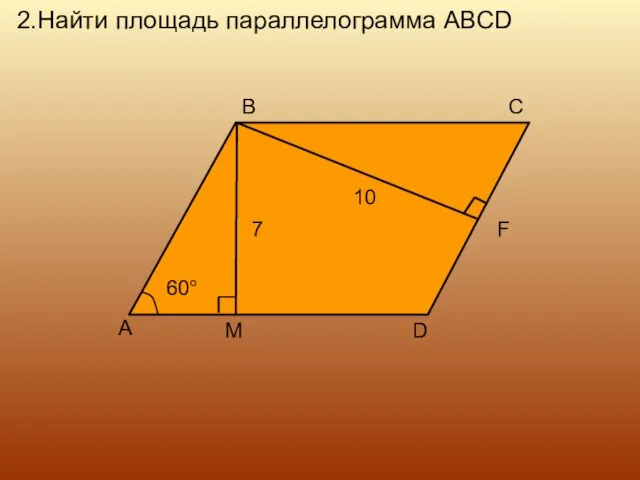
- 10. 2.Найти площадь параллелограмма ABCD
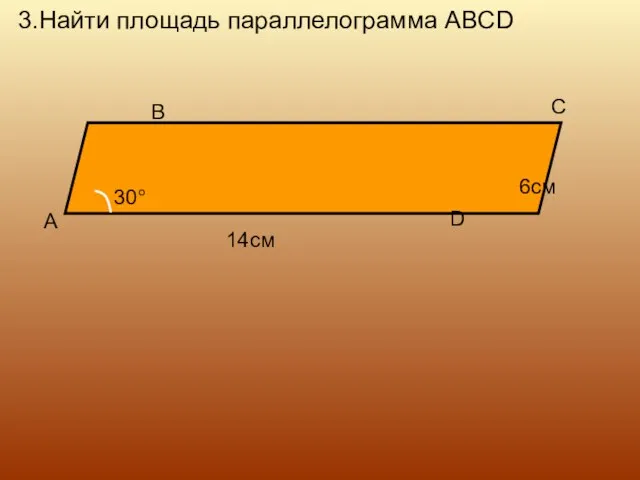
- 11. 3.Найти площадь параллелограмма ABCD
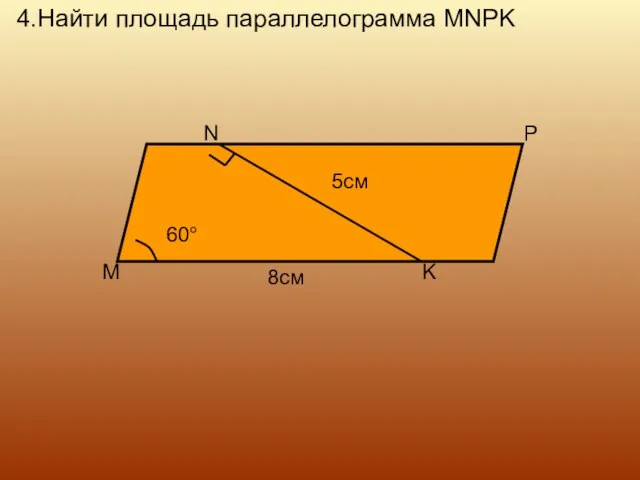
- 12. 4.Найти площадь параллелограмма MNPK
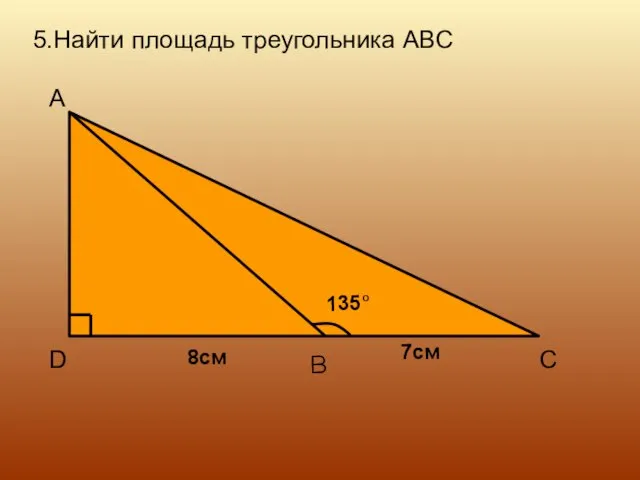
- 13. 5.Найти площадь треугольника ABC
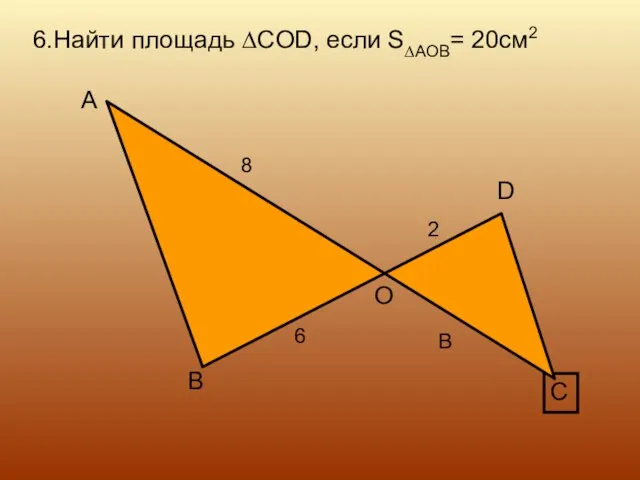
- 14. 6.Найти площадь ∆COD, если S∆AOB= 20см2
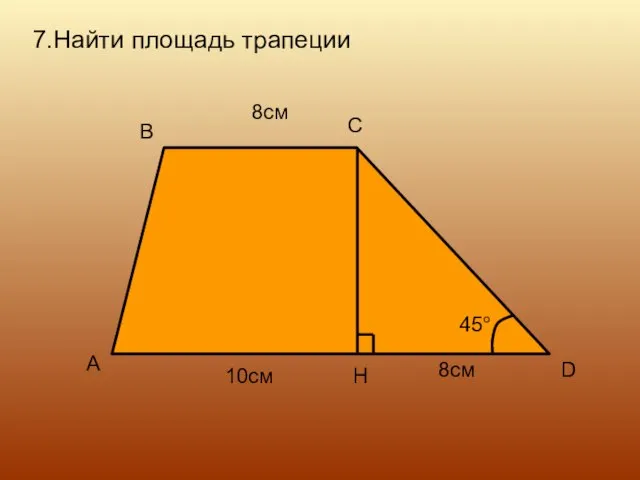
- 15. 7.Найти площадь трапеции
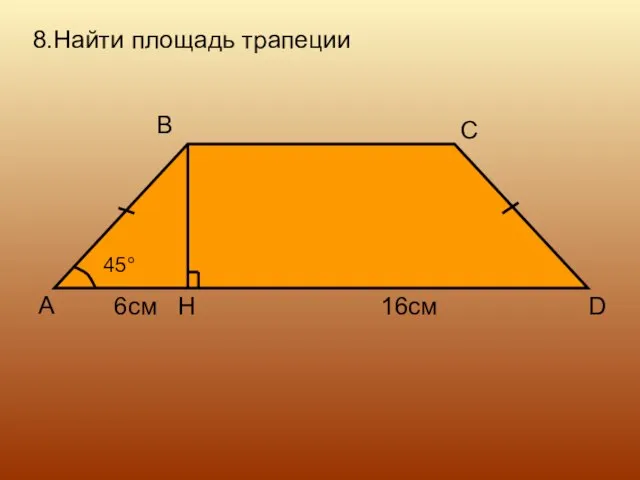
- 16. 8.Найти площадь трапеции
- 17. Самостоятельная работа Проверка выполнения работы
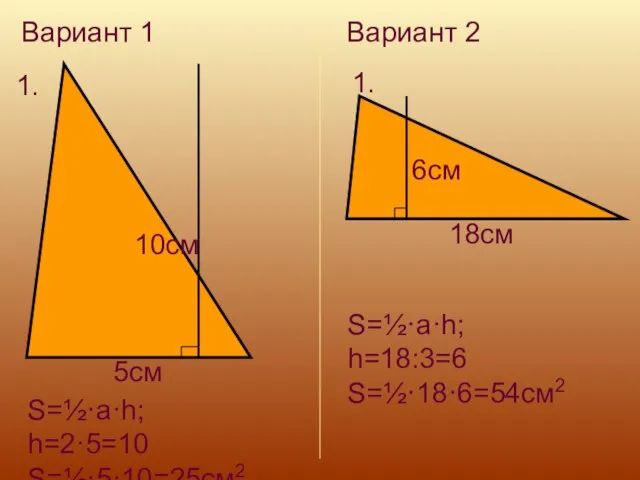
- 18. Вариант 1 1. 5см 10см S=½·a·h; h=2·5=10 S=½·5·10=25см2 Вариант 2 1. 6см 18см S=½·a·h; h=18:3=6 S=½·18·6=54см2
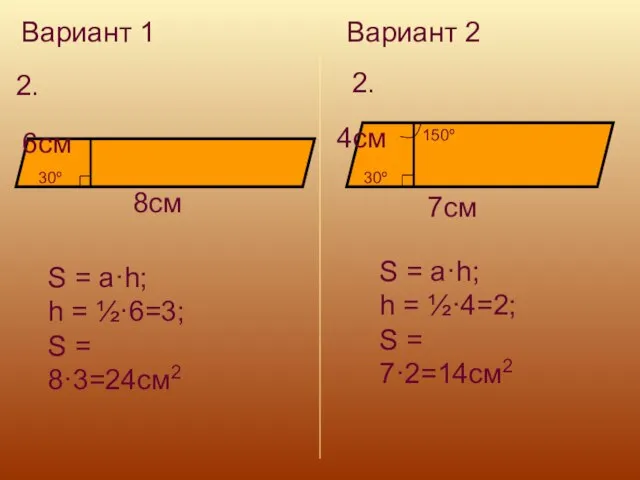
- 19. Вариант 1 Вариант 2 2. 2. 30º 8см 6см S = a·h; h = ½·6=3; S
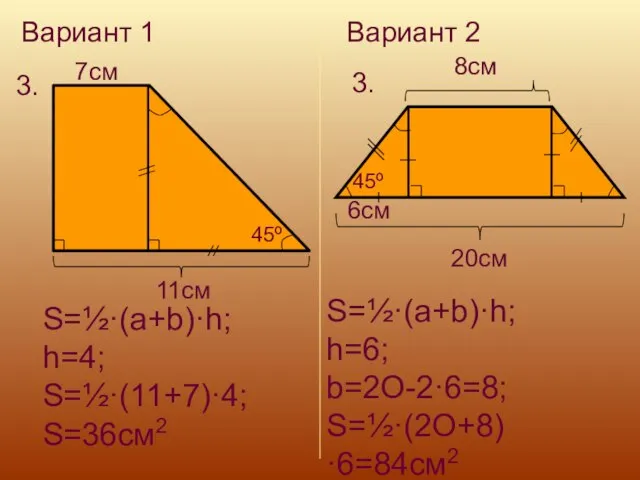
- 20. Вариант 1 Вариант 2 3. 3. 11cм 7cм 45º S=½·(a+b)·h; h=4; S=½·(11+7)·4; S=36см2 45º 20cм 6cм
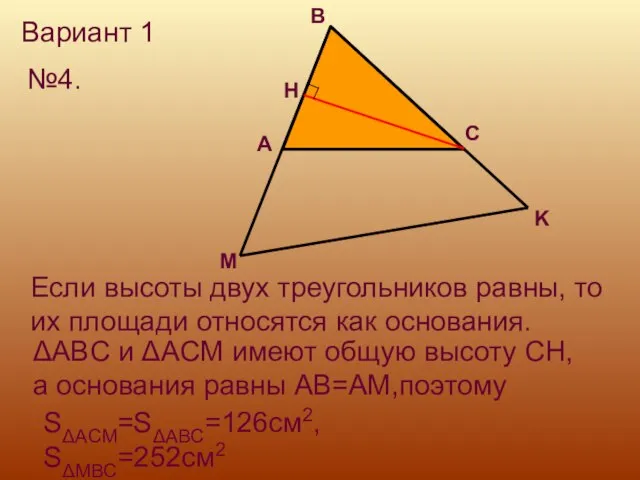
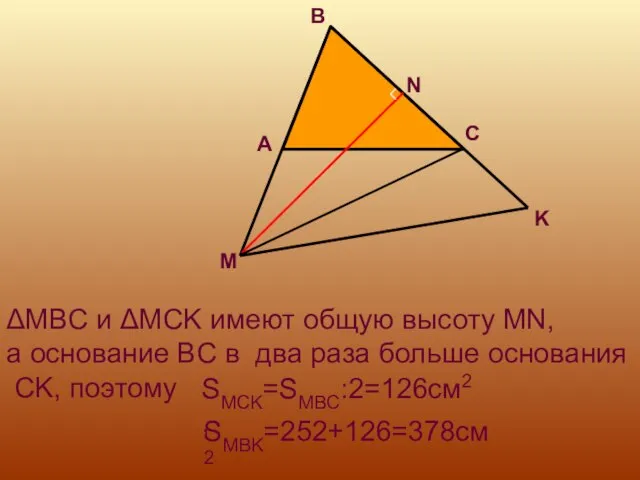
- 21. Вариант 1 №4. H Если высоты двух треугольников равны, то их площади относятся как основания. ΔABC
- 22. ΔMBC и ΔMCK имеют общую высоту MN, а основание BC в два раза больше основания CK,
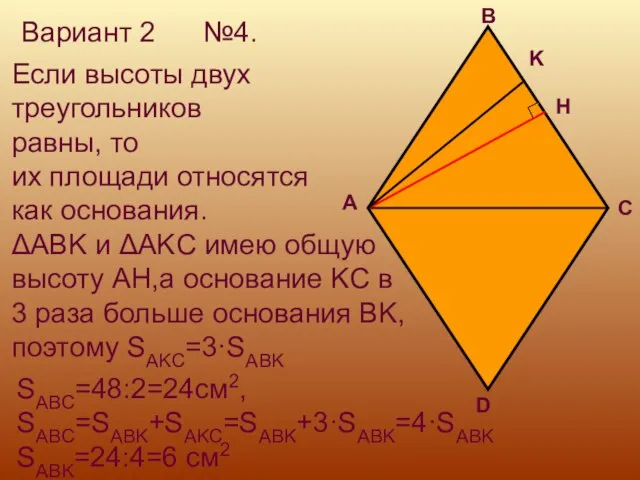
- 23. Вариант 2 №4. H K Если высоты двух треугольников равны, то их площади относятся как основания.
- 25. Скачать презентацию




 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием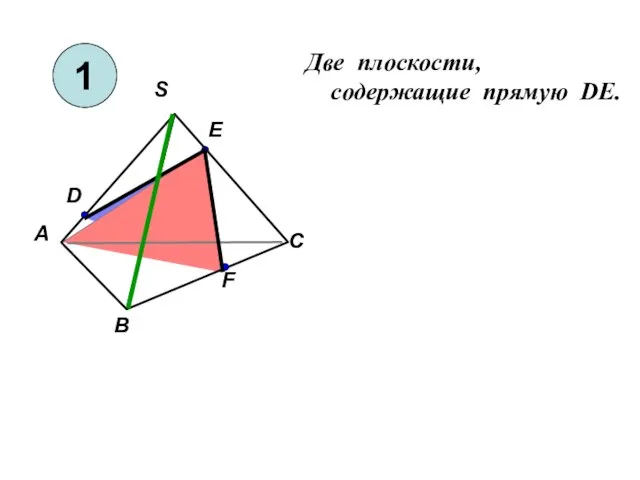 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия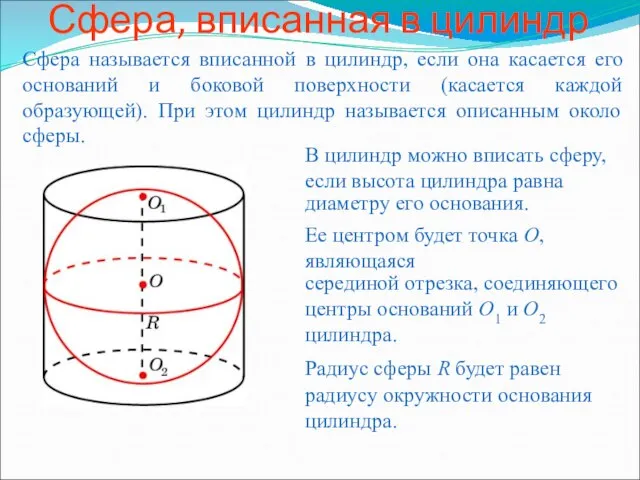 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика