Взаимное расположение прямых в пространстве

Цели урока:
Ввести определение скрещивающихся прямых.
Ввести формулировки и доказать признак и свойство скрещивающихся прямых.

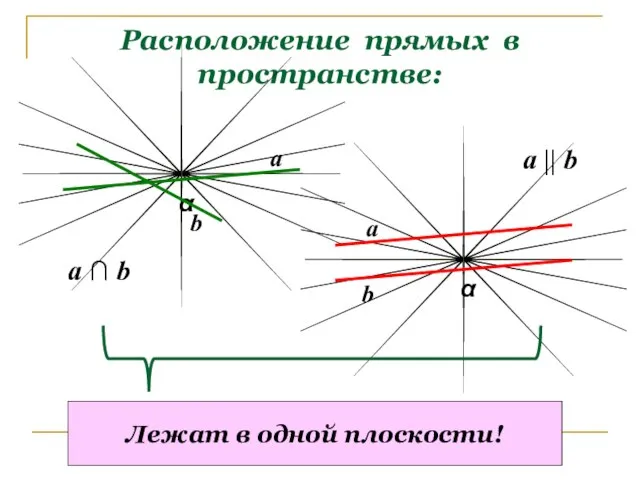
Расположение прямых в пространстве:
α
α
a
b
a
b
a ∩ b
a || b
Лежат в одной плоскости!

???
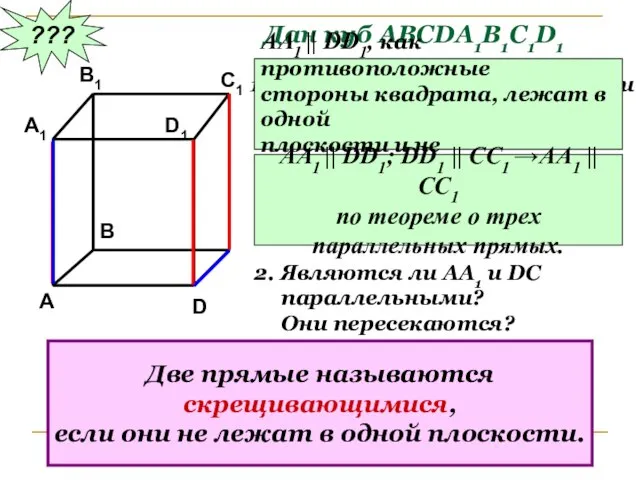
Дан куб АВСDA1B1C1D1
Являются ли параллельными
прямые АА1 и DD1; АА1 и СС1 ?
Почему?
АА1 || DD1, как противоположные
стороны квадрата, лежат в одной
плоскости и не пересекаются.
АА1 || DD1; DD1 || CC1 →AA1 || CC1
по теореме о трех
параллельных прямых.
2. Являются ли АА1 и DC
параллельными?
Они пересекаются?
Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.

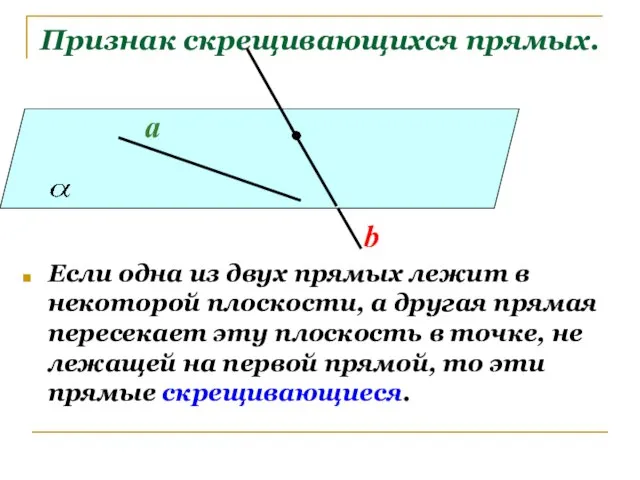
Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
a
b

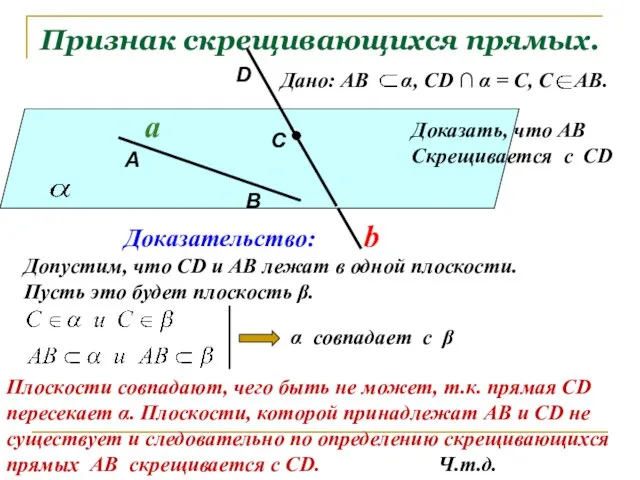
Признак скрещивающихся прямых.
Дано: АВ α, СD ∩ α = С, С АВ.
a
b
Доказательство:
Допустим, что СD и АВ лежат в одной плоскости.
Пусть это будет плоскость β.
Доказать, что АВ
Скрещивается с СD
А
В
С
D
α совпадает с β
Плоскости совпадают, чего быть не может, т.к. прямая СD
пересекает α. Плоскости, которой принадлежат АВ и СD не
существует и следовательно по определению скрещивающихся
прямых АВ скрещивается с СD. Ч.т.д.

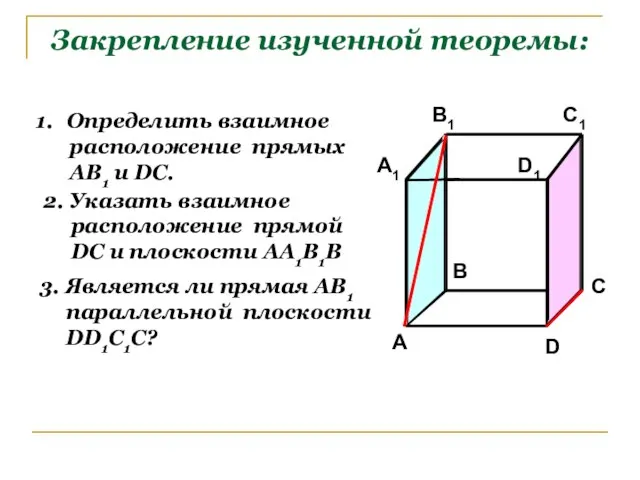
Закрепление изученной теоремы:
Определить взаимное
расположение прямых
АВ1 и DC.
2. Указать взаимное
расположение прямой
DC и плоскости АА1В1В
3. Является ли прямая АВ1
параллельной плоскости
DD1С1С?

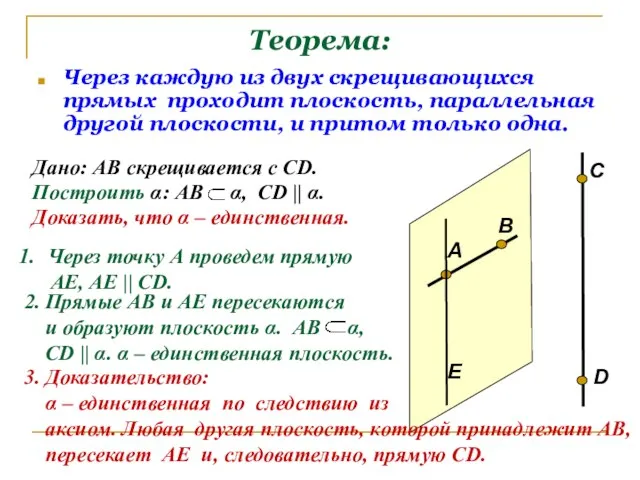
Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.
Дано: АВ скрещивается с СD.
Построить α: АВ α, СD || α.
А
В
C
D
Через точку А проведем прямую
АЕ, АЕ || СD.
Е
2. Прямые АВ и АЕ пересекаются
и образуют плоскость α. АВ α,
СD || α. α – единственная плоскость.
Доказать, что α – единственная.
3. Доказательство:
α – единственная по следствию из
аксиом. Любая другая плоскость, которой принадлежит АВ,
пересекает АЕ и, следовательно, прямую СD.

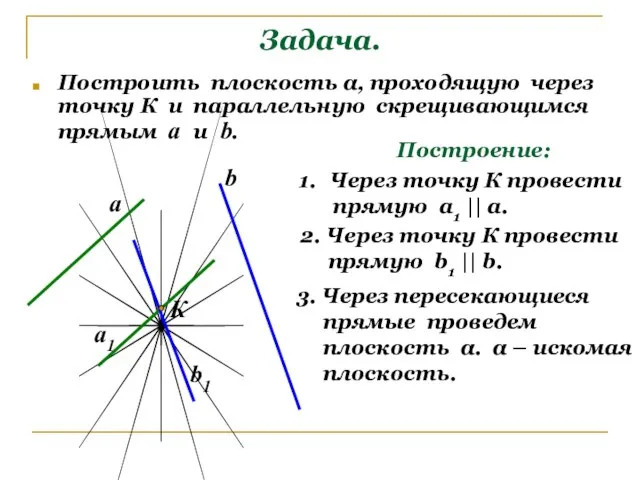
Задача.
Построить плоскость α, проходящую через точку К и параллельную скрещивающимся прямым а и b.
Построение:
Через точку К провести
прямую а1 || а.
2. Через точку К провести
прямую b1 || b.
а
b
К
а1
b1
3. Через пересекающиеся
прямые проведем
плоскость α. α – искомая
плоскость.

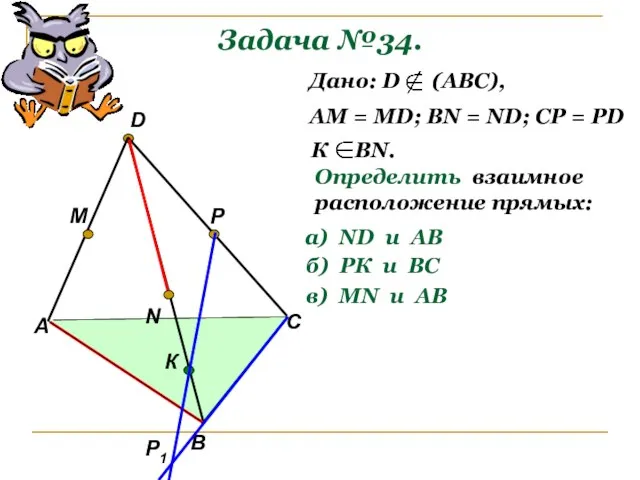
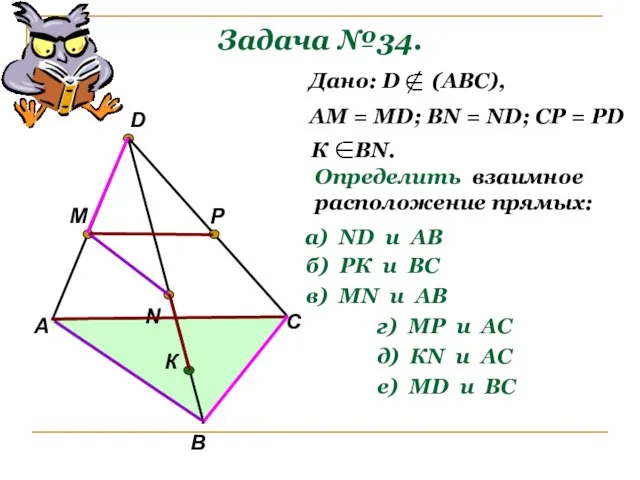
Задача №34.
А
В
С
D
M
N
P
Р1
К
Дано: D (АВС),
АМ = МD; ВN = ND; CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB

Задача №34.
А
В
С
D
M
N
P
К
Дано: D (АВС),
АМ = МD; ВN = ND; CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
г) МР и AС
д) КN и AС
е) МD и BС