Содержание
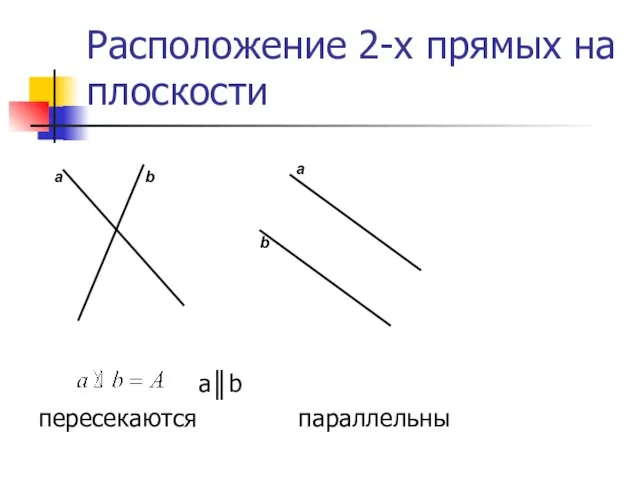
- 2. Расположение 2-х прямых на плоскости а║b пересекаются параллельны a b a b
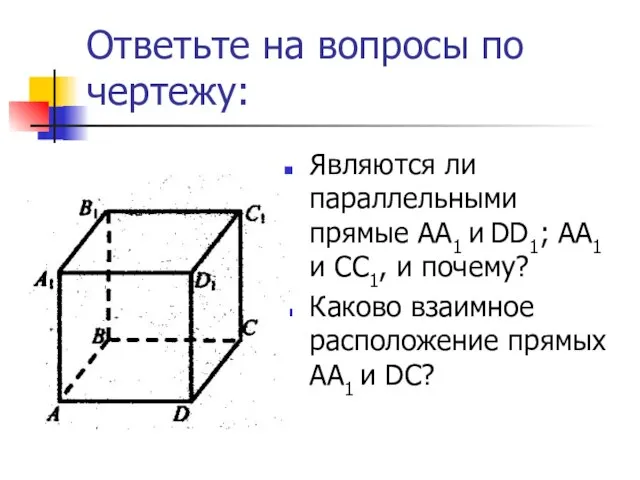
- 3. Ответьте на вопросы по чертежу: Являются ли параллельными прямые АА1 и DD1; АА1 и CC1, и
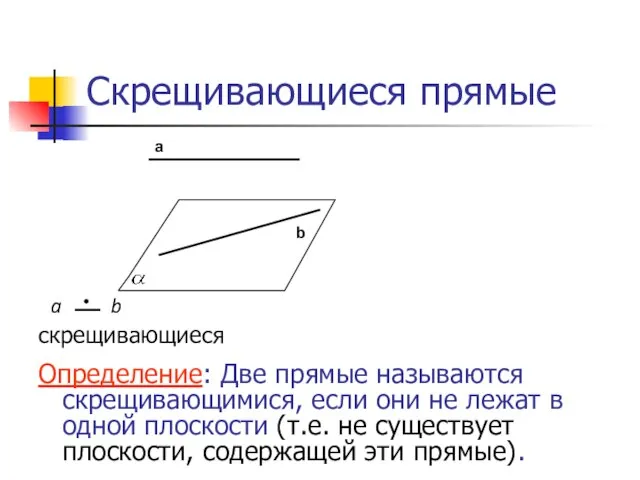
- 4. Скрещивающиеся прямые скрещивающиеся Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости (т.е.
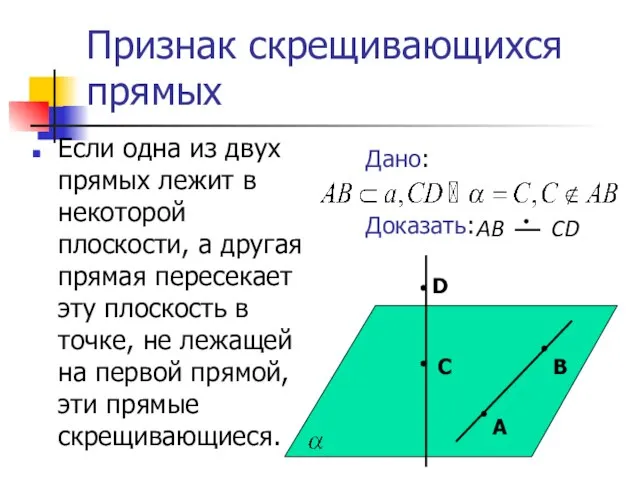
- 5. Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает
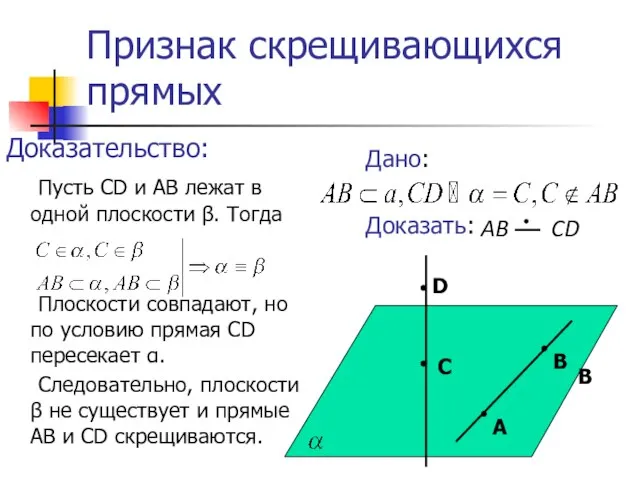
- 6. Признак скрещивающихся прямых Доказательство: Пусть CD и АВ лежат в одной плоскости β. Тогда Плоскости совпадают,
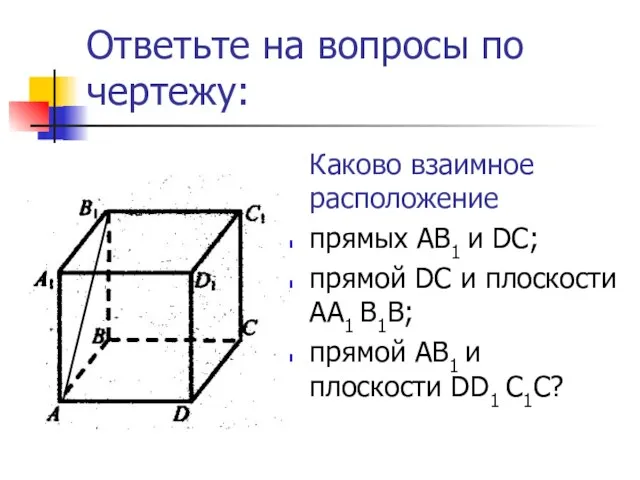
- 7. Ответьте на вопросы по чертежу: Каково взаимное расположение прямых AB1 и DС; прямой DС и плоскости
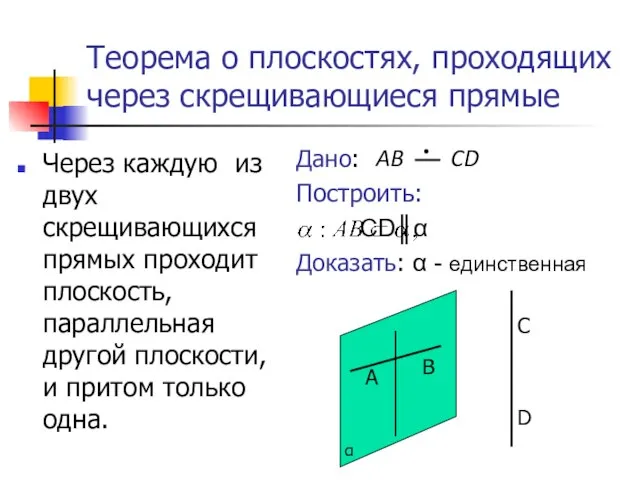
- 8. Теорема о плоскостях, проходящих через скрещивающиеся прямые Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная
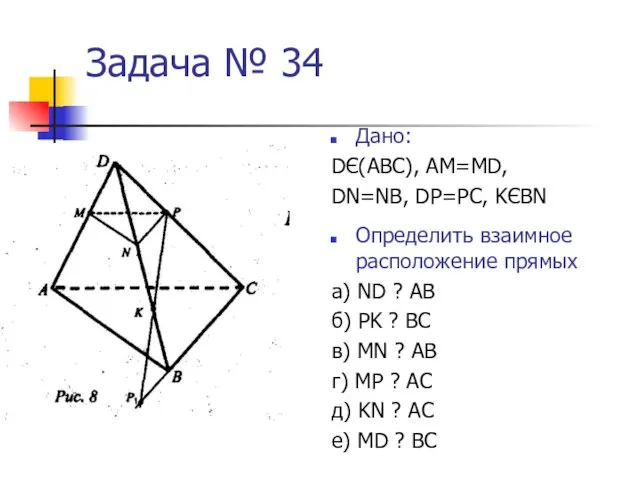
- 9. Задача № 34 Дано: DЄ(АВС), АМ=МD, DN=NB, DP=PC, KЄBN Определить взаимное расположение прямых а) ND ?
- 10. Задача № 39 Дано: Доказать: Доказательство: 1) {A,C,D}Єα по аксиоме А1 2) В¢α, так как по
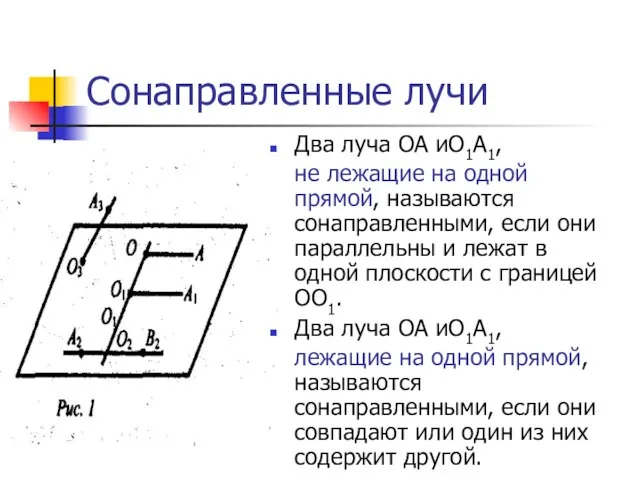
- 11. Сонаправленные лучи Два луча ОА иО1А1, не лежащие на одной прямой, называются сонаправленными, если они параллельны
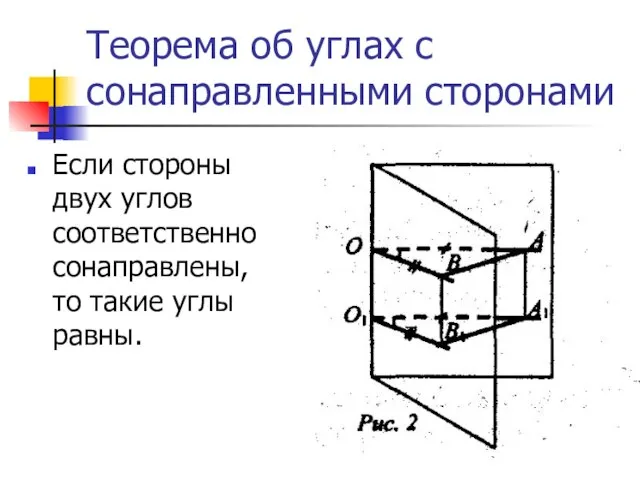
- 12. Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны.
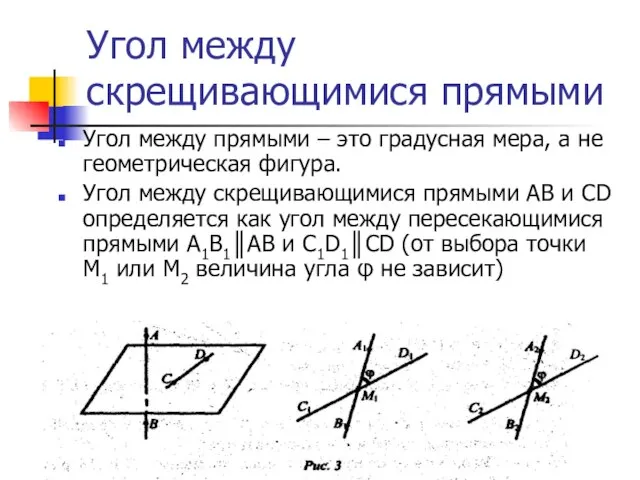
- 13. Угол между скрещивающимися прямыми Угол между прямыми – это градусная мера, а не геометрическая фигура. Угол
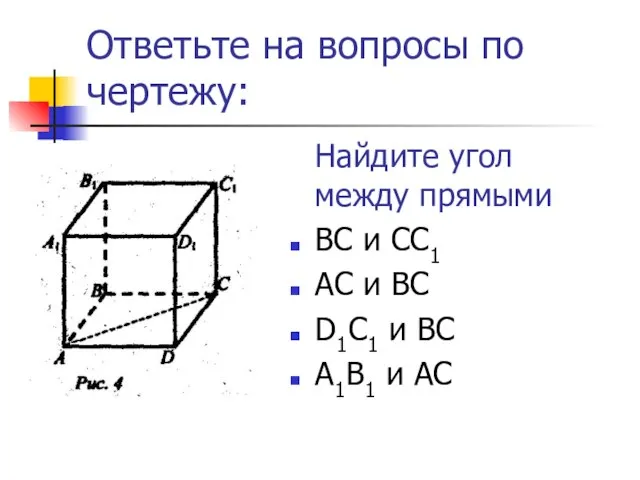
- 14. Ответьте на вопросы по чертежу: Найдите угол между прямыми ВС и СС1 АС и ВС D1C1
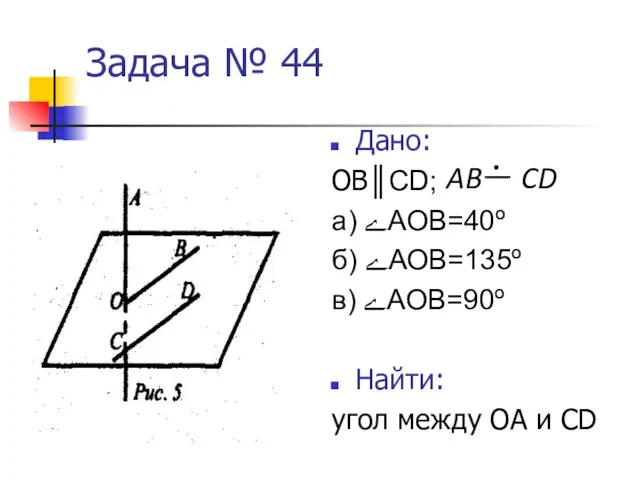
- 15. Задача № 44 Дано: ОВ║CD; а) ﮮАОВ=40º б) ﮮАОВ=135º в) ﮮАОВ=90º Найти: угол между ОА и
- 17. Скачать презентацию

 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием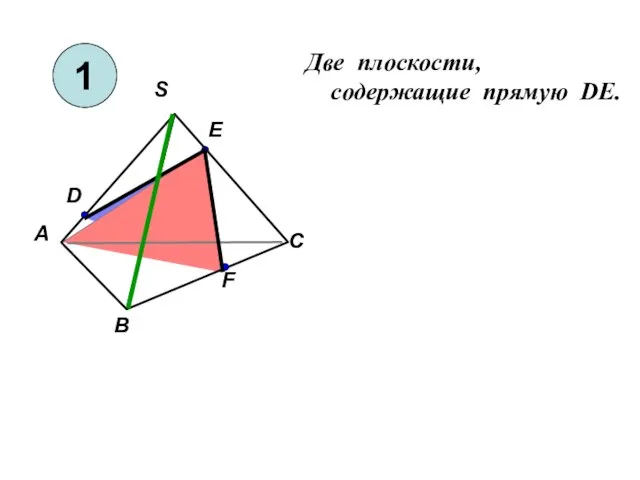 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия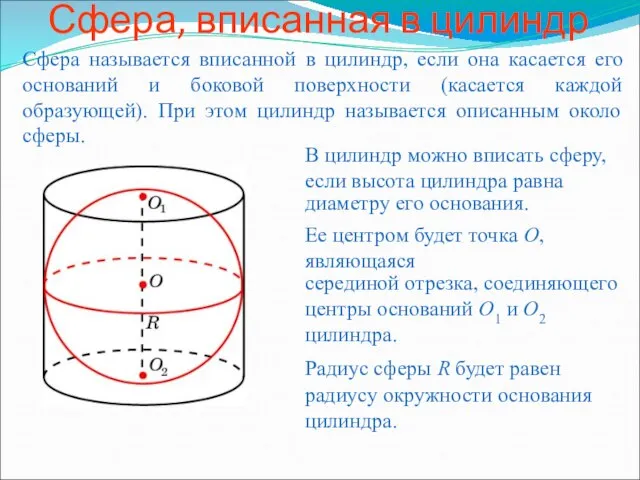 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика