Содержание
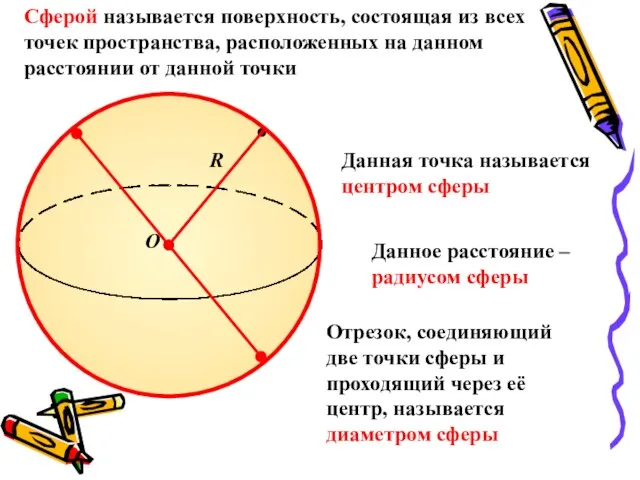
- 2. R O Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной
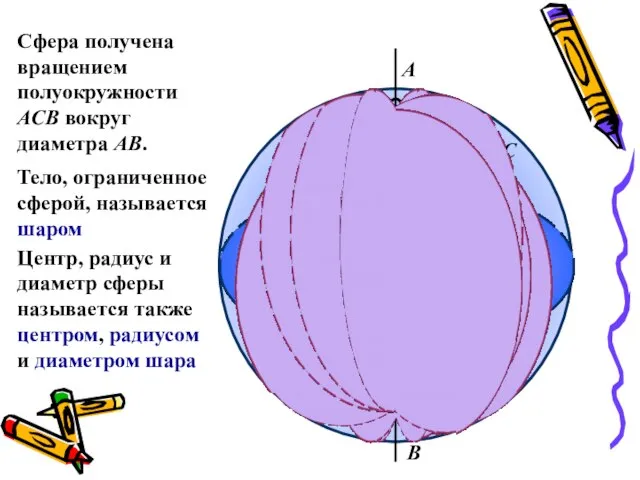
- 3. Сфера получена вращением полуокружности АСВ вокруг диаметра АВ. А С В Тело, ограниченное сферой, называется шаром
- 4. R M(x;y;z) C(x0;y0;z0) z y x O Уравнение сферы Уравнение с тремя неизвестными x, y и
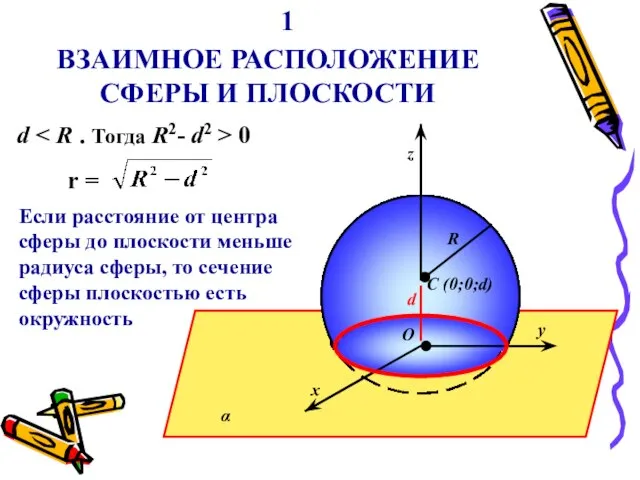
- 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ α y x z C (0;0;d) O R 1 d 0
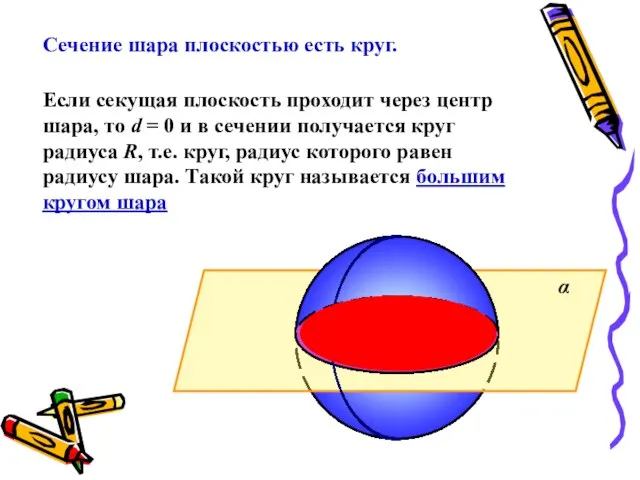
- 6. α R O Сечение шара плоскостью есть круг. Если секущая плоскость проходит через центр шара, то
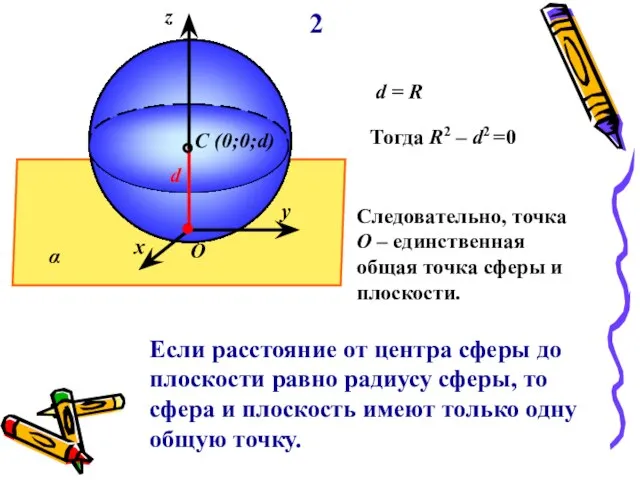
- 7. O d C (0;0;d) α y x z d = R Тогда R2 – d2 =0
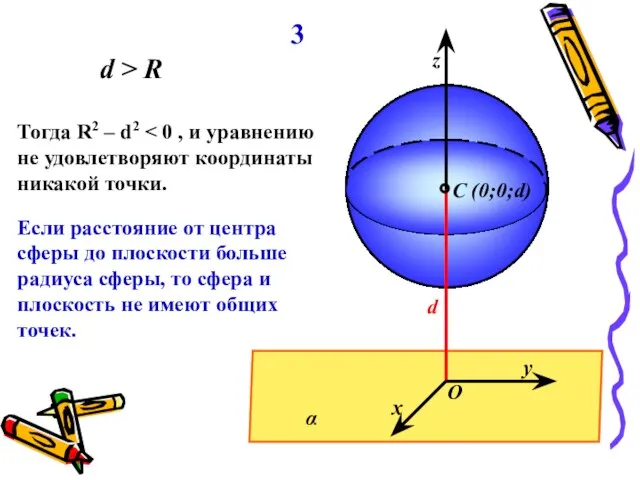
- 8. α y x d z C (0;0;d) O 3 d > R Тогда R2 – d2
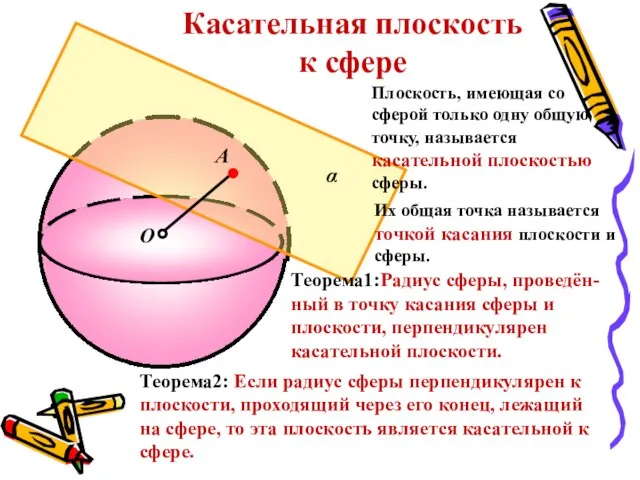
- 9. α О А Касательная плоскость к сфере Плоскость, имеющая со сферой только одну общую точку, называется
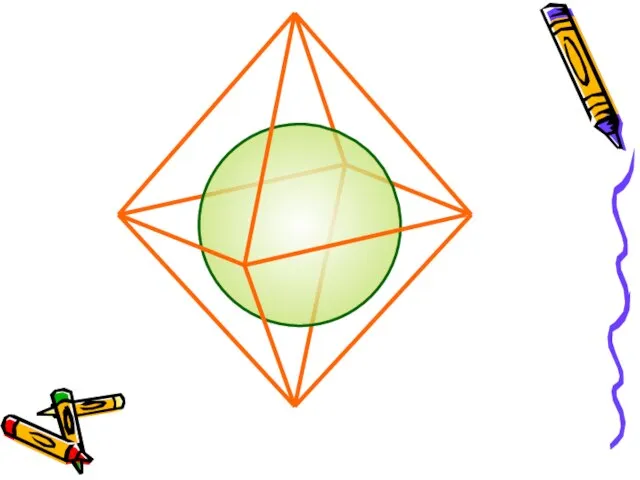
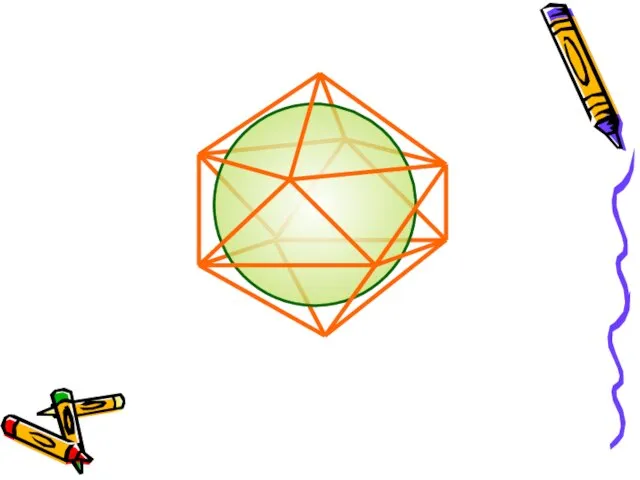
- 10. За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю
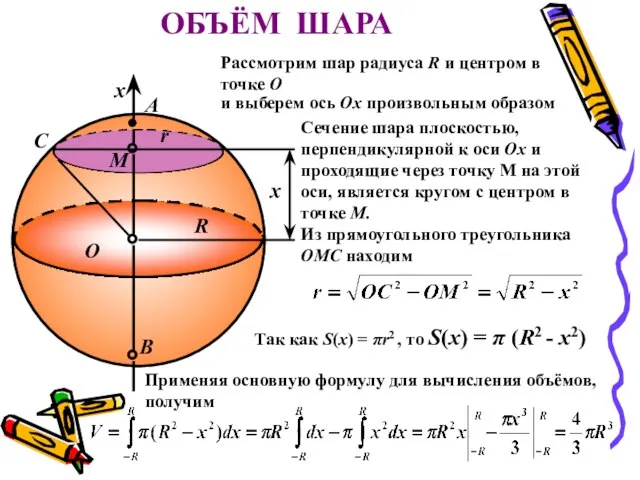
- 14. B O R r x M A x С ОБЪЁМ ШАРА Рассмотрим шар радиуса R и
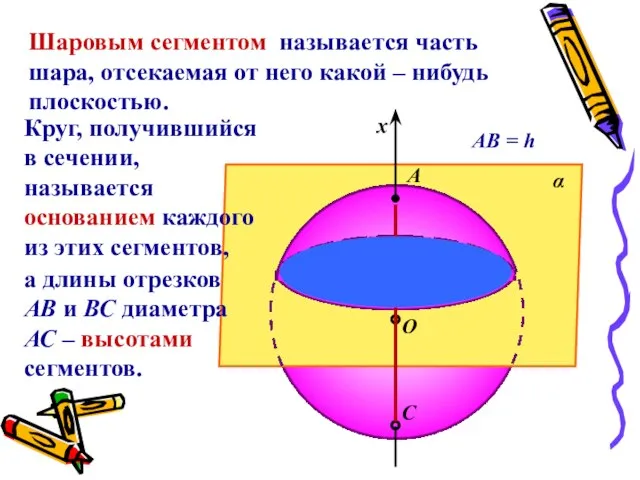
- 15. С О В α х АВ = h А Шаровым сегментом называется часть шара, отсекаемая от
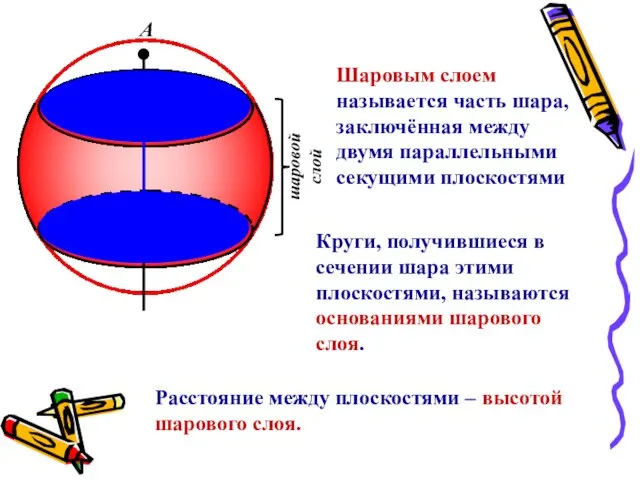
- 16. шаровой слой С В А Шаровым слоем называется часть шара, заключённая между двумя параллельными секущими плоскостями
- 18. Скачать презентацию


 Треугольники. Третий признак равенства
Треугольники. Третий признак равенства Геометрия в древние и новые века
Геометрия в древние и новые века Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Треугольники 3 класс
Треугольники 3 класс Понятие цилиндра
Понятие цилиндра Логические законы и правила
Логические законы и правила Объем конуса цилиндра
Объем конуса цилиндра Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Измерение длин отрезков
Измерение длин отрезков Скалярное произведение векторов
Скалярное произведение векторов Полезные теоремы, следствия и задачи.
Полезные теоремы, следствия и задачи. Перпендикулярные прямые 7 класс
Перпендикулярные прямые 7 класс Шар, вписанный в пирамиду, призму, конус
Шар, вписанный в пирамиду, призму, конус Смежные и вертикальные углы
Смежные и вертикальные углы Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Вычисление площадей фигур в ходе экспериментальной деятельности
Вычисление площадей фигур в ходе экспериментальной деятельности Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Многогранники: виды задач и методы их решения (типовые задания С2) - 1 Правильный додекаэдр
Правильный додекаэдр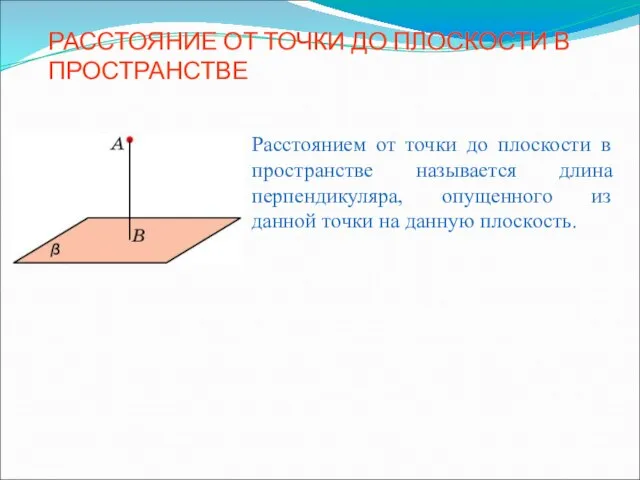 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Презентация Презентация к уроку геометрии 8 класса по теме: «Пропорциональные отрезки в прямоугольном треугольнике» (урок-кве
Презентация Презентация к уроку геометрии 8 класса по теме: «Пропорциональные отрезки в прямоугольном треугольнике» (урок-кве Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Многогранники вокруг нас
Многогранники вокруг нас Классификация геометрических объектов
Классификация геометрических объектов Круги Эйлера и их практическое применение
Круги Эйлера и их практическое применение Что такое геометрия
Что такое геометрия Двугранный угол (10-11 класс) - презентация по Геометрии_
Двугранный угол (10-11 класс) - презентация по Геометрии_ Стереометрия в образах
Стереометрия в образах