что |OA’| = |OB’| = |OC’|
Тогда треугольники A’OB’, B’OC’ и С’OA’ –
равнобедренные, а их углы при основаниях 1 – 6 – острые.
Для трехгранных углов с вершинами A’, B’ и C’ применим
неравенства, доказанные в пункте I:
∠С’А’B’ < ∠1 + ∠6; ∠А’B’C’ < ∠2 + ∠3; ∠B’С’А’ < ∠4 + ∠5.
Сложим эти неравенства почленно,
тогда 180° < (∠1 + ∠2) + (∠3 + ∠4) + (∠5 + ∠6) =
= (180° – γ) + (180° – α) + (180° – β) ⇒ α + β + γ < 360°.
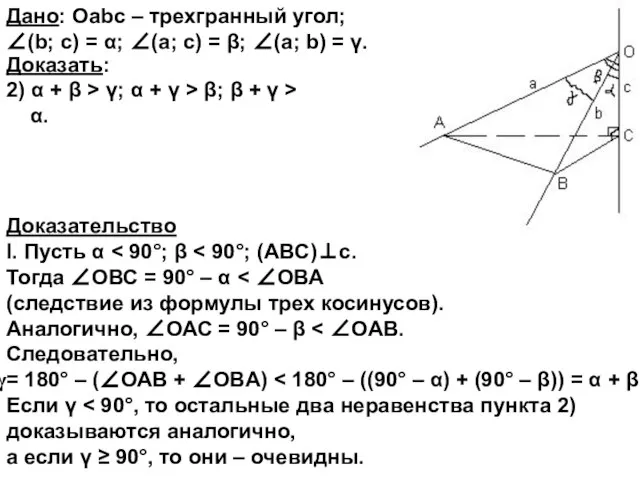
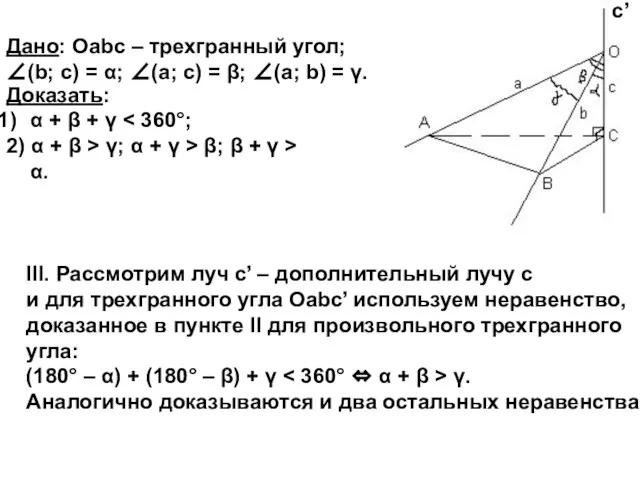
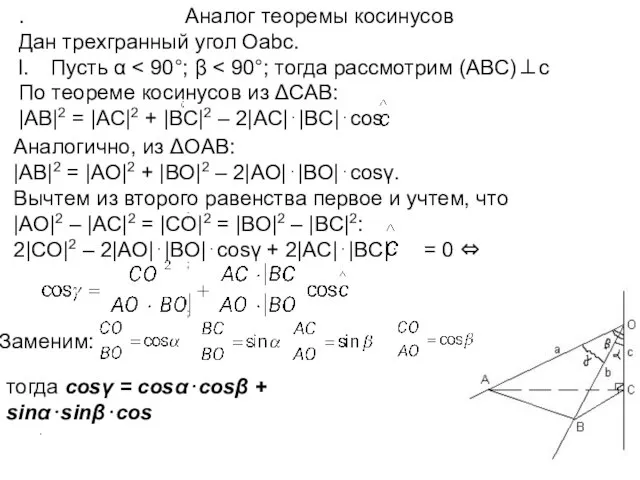
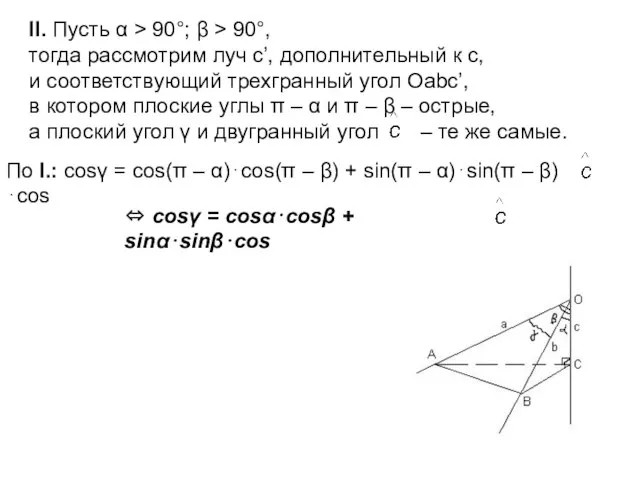
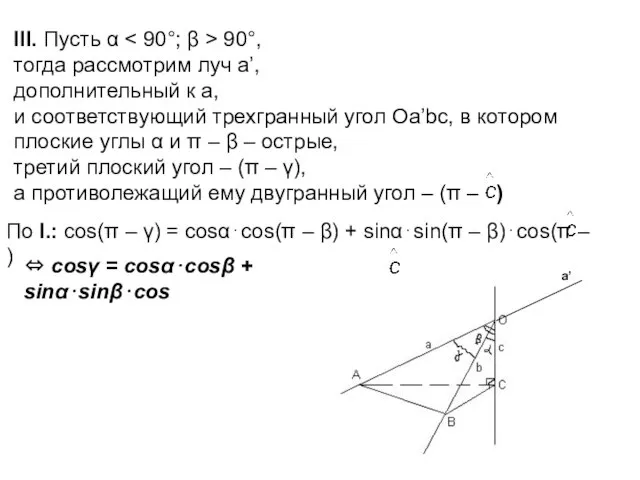
Дано: Оabc – трехгранный угол;
∠(b; c) = α; ∠(a; c) = β; ∠(a; b) = γ.
Доказать:
α + β + γ < 360°;
2) α + β > γ; α + γ > β; β + γ > α.





 Площадь прямоугольного треугольника
Площадь прямоугольного треугольника Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А.
Проект ученицы 5 «А» класса Горбуновой Ксении Учитель: Чижевская М.А. Циклоида
Циклоида Площади фигур. Зачёт
Площади фигур. Зачёт Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Решение прямоугольных треугольников
Решение прямоугольных треугольников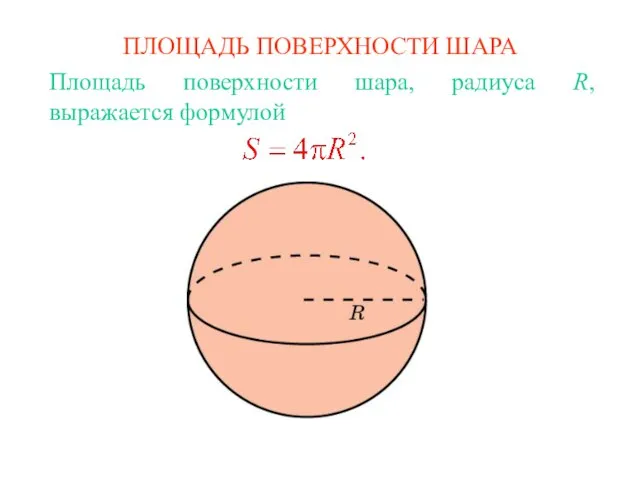 Площадь поверхности шара
Площадь поверхности шара Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Скрещивающиеся прямые
Скрещивающиеся прямые Флексагоны флексоры
Флексагоны флексоры Сфера. Шар
Сфера. Шар Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ От сферы к плоскости
От сферы к плоскости Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Правильные многогранники
Правильные многогранники Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Чудеса симметрии
Чудеса симметрии Логарифм. Основные понятия
Логарифм. Основные понятия Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Геометрия в жизни
Геометрия в жизни Египетский треугольник
Египетский треугольник Задачи на построение сечений
Задачи на построение сечений История возникновения Геометрии
История возникновения Геометрии История геометрии
История геометрии Задачи на готовых чертежах
Задачи на готовых чертежах Сечения
Сечения Площади плоских геометрических фигур
Площади плоских геометрических фигур