Касательная к окружности 7 класс

Взаимное расположение
прямой и окружности
d – расстояние от центра окружности до прямой.

O
R
S
C
M
K
F
T
A
D
B
Q
N
X
Назови: радиус, диаметр, хорду, касательную, секущую

Теорема. Касательная к окружности перпендикулярна к
радиусу, проведённому в точку касания.
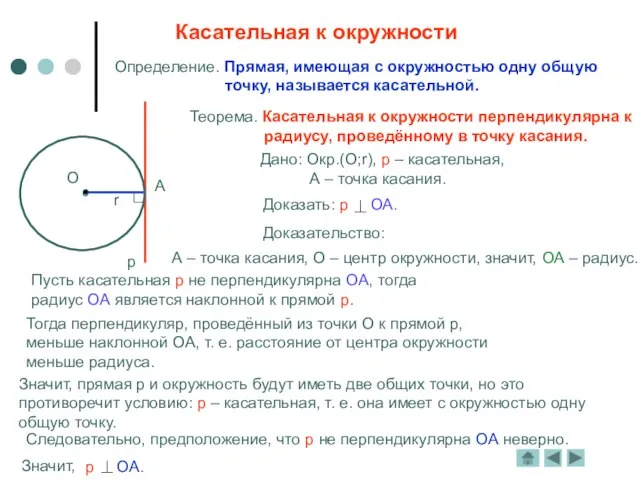
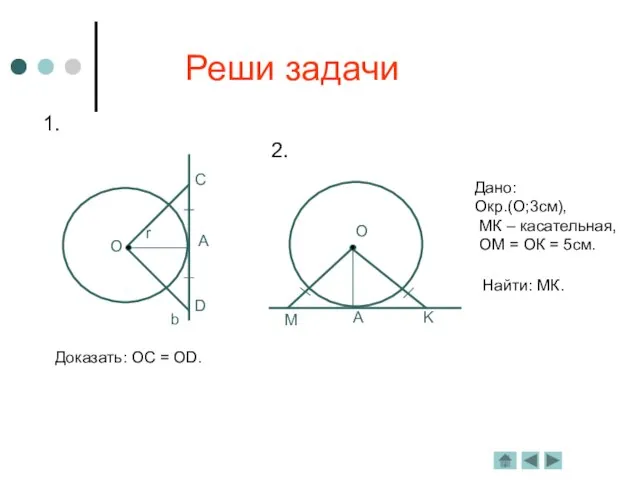
Дано: Окр.(О;r), р – касательная,
А – точка касания.
Доказательство:
А – точка касания, О – центр окружности, значит, ОА – радиус.
Пусть касательная р не перпендикулярна ОА, тогда
радиус ОА является наклонной к прямой р.
Тогда перпендикуляр, проведённый из точки О к прямой р,
меньше наклонной ОА, т. е. расстояние от центра окружности
меньше радиуса.
Значит, прямая р и окружность будут иметь две общих точки, но это
противоречит условию: р – касательная, т. е. она имеет с окружностью одну
общую точку.
Следовательно, предположение, что р не перпендикулярна ОА неверно.
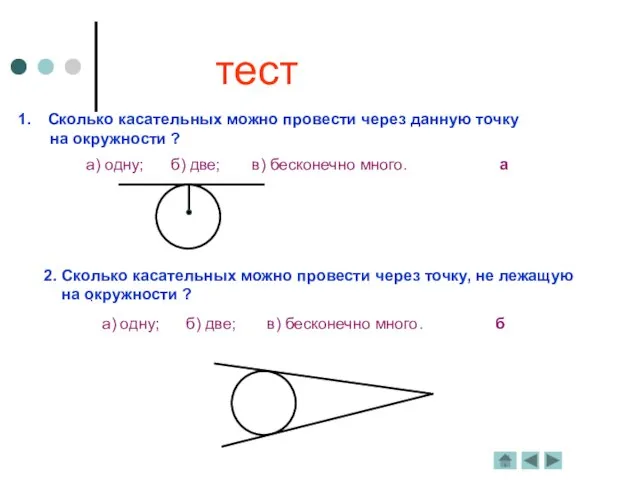
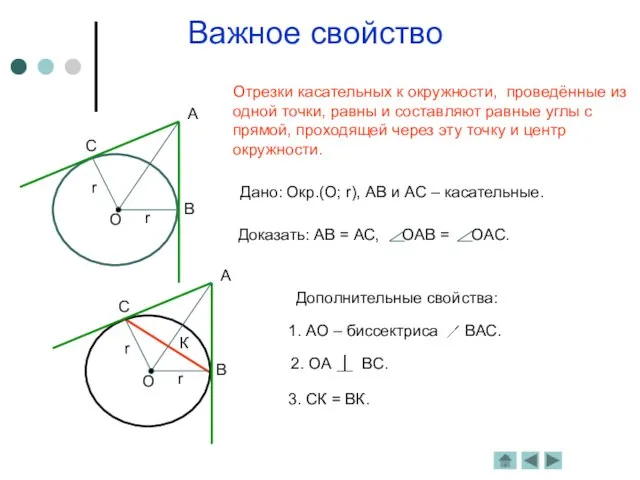
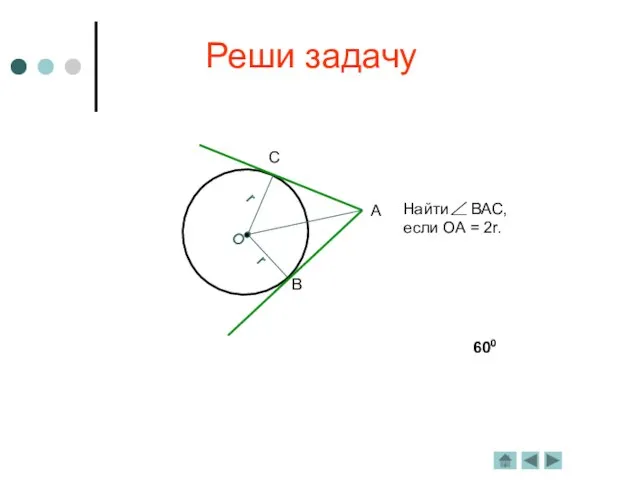
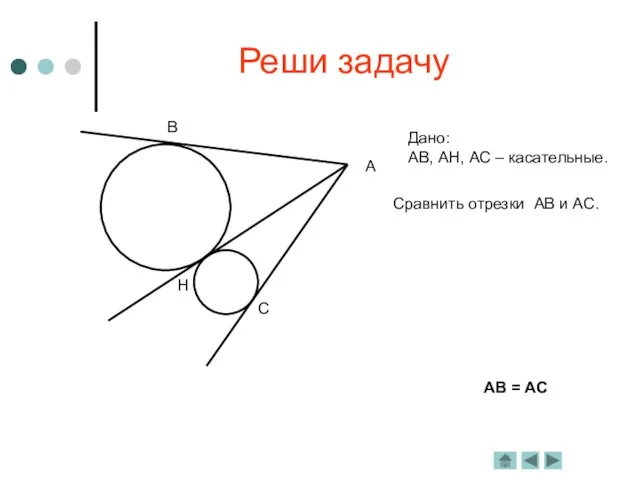
Касательная к окружности
Определение. Прямая, имеющая с окружностью одну общую
точку, называется касательной.

Определи вид треугольника АВС.
Дано:
АВ – касательная,
ВС – диаметр.

тест
Сколько касательных можно провести через данную точку
на окружности ?
а) одну; б) две; в) бесконечно много.
2. Сколько касательных можно провести через точку, не лежащую
на окружности ?
а
а) одну; б) две; в) бесконечно много.
б
.

3. Сколько окружностей можно провести, касающихся данной прямой ?
а) одну; б) две; в) бесконечно много.
в
тест

4. Сколько окружностей можно провести, касающихся данной прямой в данной точке ?
в
а) одну; б) две; в) бесконечно много.
тест

5. Сколько окружностей данного радиуса можно провести, касающихся данной прямой в данной точке ?
а) одну; б) две; в) бесконечно много.
б
тест

Реши задачи

Важное свойство
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр
окружности.
Дано: Окр.(О; r), АВ и АС – касательные.
Дополнительные свойства:
3. СК = ВК.

Реши задачу
600

Реши задачу
АВ = АС

Реши задачу

Реши задачу

Реши задачу
1 : 1

Если прямая проходит через конец радиуса,
лежащий на окружности, и перпендикулярна
к этому радиусу, то она является касательной.
(теорема, обратная к свойству касательной)
Признак касательной
Доказать: АВ – касательная.
Доказательство:
и, следовательно, прямая и окружность имеют
только одну общую точку.
По определению касательной и будет прямая АВ.

Реши задачу
Доказать, что все стороны треугольника КНМ касаются окружности.