Теорема синусов и косинусов в задачах с практическим содержанием

Цели урока:
1) выработать умения и навыки решения задач с практическим содержанием, применяя теоремы;
2) показать связь теории с практикой;
3) продолжать вырабатывать внимание, активность, аккуратность, самостоятельность.

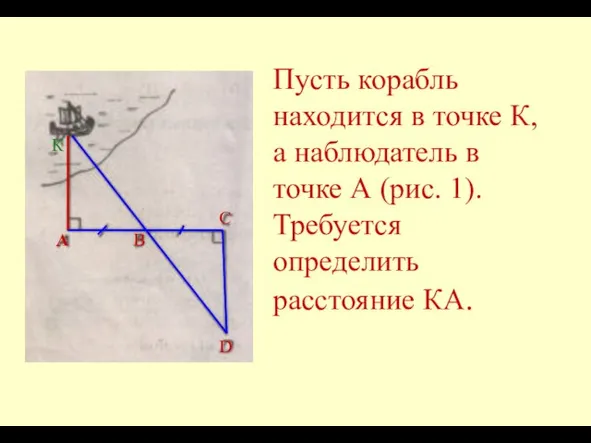
Пусть корабль находится в точке К, а наблюдатель в точке А (рис. 1). Требуется определить расстояние КА.
А
К
B
C
D

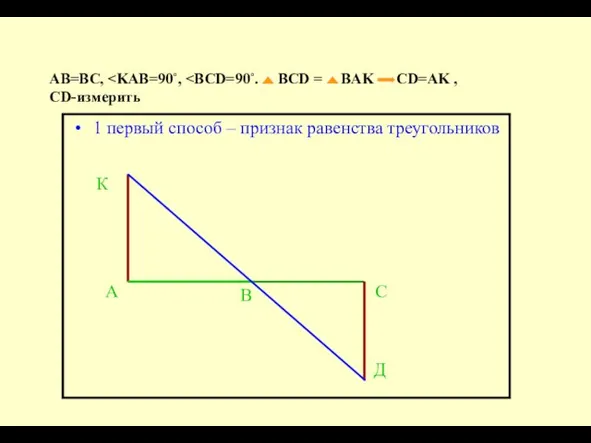
АВ=ВС,
1 первый способ – признак равенства треугольников

Второй способ – метод триангуляции (применение - астрономия)
1. Измерение углов α и β и расстояния АВ.
2. Построение треугольников А'В'К' с углами α и β при вершинах А' и В' соответственно.
3. АВК и А'В'К‘ подобны, АК:АВ=А'К' :А'В‘, длины АВ, А'К' и А'В‘ известны, то АК =(АВ* А'К'): А'В‘
β
α

Третий способ – русская военная инструкция начала XVII в.
Необходимо измерить расстояние от точки А до т. В.
В т.А вбить «жезл» примерно в рост человека.
Верхний конец «жезла» следует совместить c вершиной прямого угла треугольника так, чтобы продолжение одного из катетов проходило через т.В.
т.С – т. пересечение другого катета с землей.
АВ: АD= АD:АС
АВ =
В
D
A
С

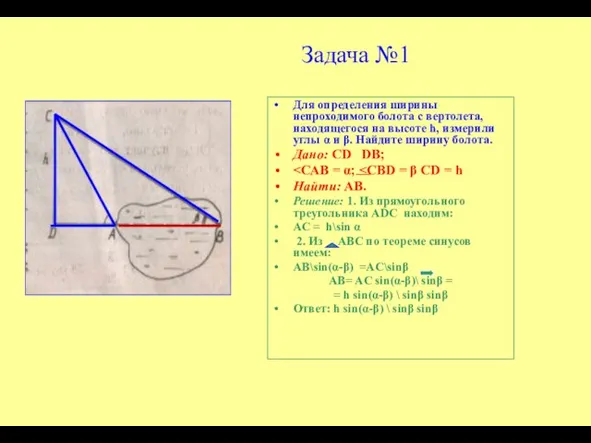
Задача №1
Для определения ширины непроходимого болота с вертолета, находящегося на высоте h, измерили углы α и β. Найдите ширину болота.
Дано: СD ‌ DВ;
<САВ = α; <СВD = β СD = h
Найти: АВ.
Решение: 1. Из прямоугольного треугольника АDC находим:
АС = h\sin α
2. Из АВС по теореме синусов имеем:
АВ\sin(α-β) =AC\sinβ
AB= AC sin(α-β)\ sinβ =
= h sin(α-β) \ sinβ sinβ
Ответ: h sin(α-β) \ sinβ sinβ

Задача №2
Вершина горы видна из точки А под углом 38°42’, а при приближении к горе на 200 м вершина стала видна под углом 42°. Найти высоту горы.
Дано: АВ = 200 м, <САВ = α = 38°42’; <СВD = β= 42°; СD DA
Найти: СD.
Решение. 1. Из СВА по теореме синусов имеем равенство CD\ sin α = AB\ sinγ , откуда
CB = AB sin α\ sinγ.
2. Угол β — внешний угол АВС, поэтому β = α +γ, откуда γ = β – α.
3. СВ = 200 sinα\sin(β-α) .
4. Из СВD находим
СD = СВsinβ = 200 sinα sinβ\ sin(β-α) = 14325 м.
Ответ: СD = 14 325 м.

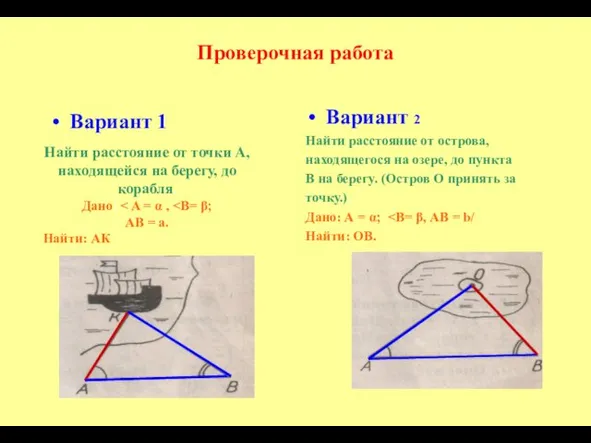
Проверочная работа
Вариант 1
Вариант 2
Найти расстояние от острова,
находящегося на озере, до пункта
В на берегу. (Остров О принять за
точку.)
Дано: А = α;
Найти: ОВ.
Найти расстояние от точки А, находящейся на берегу, до корабля.
Дано: < A = α ,
AB = a.
Найти: АК