Объёмы и поверхности тел вращения

Тела вращения

оглавление
1.Виды тел вращения
2.Определения тел вращения:
а)цилиндр
б)конус
в)шар
3.Сечения тел вращения:
а)цилиндр
б)конус
в)шар
4.Объёмы тел вращения
5.Площади поверхностей тел вращения
Завершить работу

ВИДЫ ТЕЛ ВРАЩЕНИЯ
Цилиндр-тело, которое описывает прямоугольник при вращении его около стороны как оси
Конус-тело, которое получено при вращении прямоугольного треугольника вокруг его катета как оси
Шар-тело полученное при вращении полукруга вокруг его диаметра как оси

ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги называются основаниями цилиндра, а отрезки,соединяющие соответствующие точки окружностей кругов,образующими цилиндра.

ОПРЕДЕЛЕНИЕ КОНУСА
Конусом называется тело,которое состоит из круга-основания конуса,точки, не лежащей в плоскости этого круга,вершины конуса и всех отрезков,соединяющих вершину конуса с точками основания.

СЕЧЕНИЯ ЦИЛИНДРА
Сечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник.
Осевое сечение-сечение цилиндра плоскостью,проходящей через его ось
Сечение цилиндра плоскостью, параллельной основаниям, представляет собой круг.

ОПРЕДЕЛЕНИЕ ШАРА
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии,не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.

СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью,проходящей через его вершину, представляет собой равнобедренный треугольник.
Осевое сечение конуса-это сечение, проходящее через его ось.
Сечение конуса плоскостью, параллельной его основаниям, представляет собой круг с центром на оси конуса.

СЕЧЕНИЯ ШАРА
Сечение шара плоскостью есть круг. Центр этого шара есть основание перпендикуляра,опущенного из центра шара на секущую плоскость.
Сечение шара диаметральной плоскостью называется большим кругом.

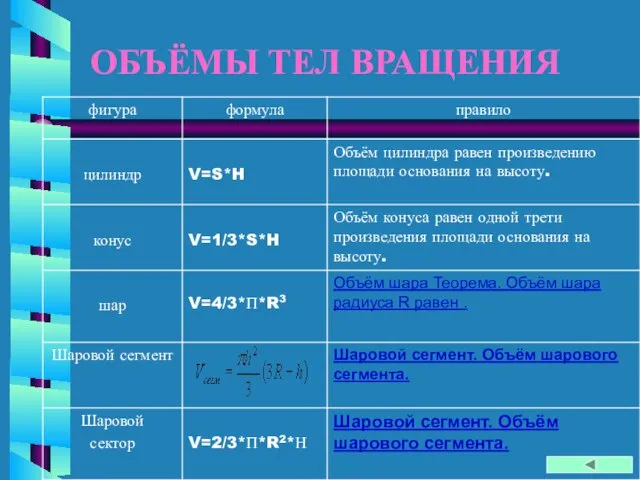
ОБЪЁМЫ ТЕЛ ВРАЩЕНИЯ

ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ

Объём шара
Теорема. Объём шара радиуса R равен .
Доказательство. Рассмотрим шар радиуса R с центром в точке О и выберем ось Ох произвольным образом (рис. ). Сечение шара плоскостью, перпендикулярной к оси Ох и проходя­щей через точку М этой оси, является кругом с центром в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим:
(2.6.1)
Так как , то (2.6.2)
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х,удовлетворяющих условию . Применяя основную формулу для вычисления объемов тел при
, получим
Теорема доказана.

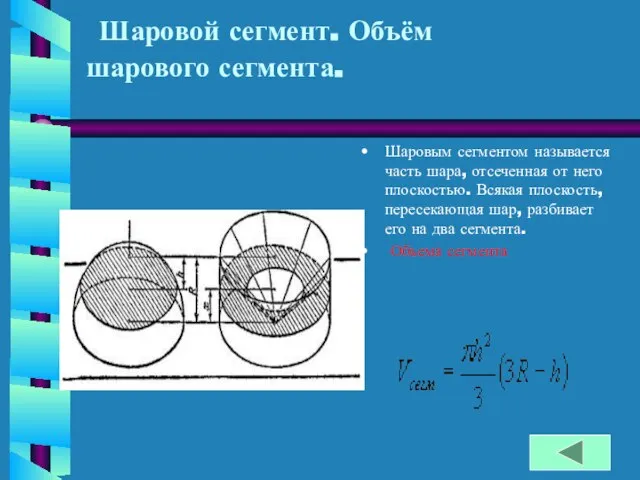
Шаровой сегмент. Объём шарового сегмента.
Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Всякая плоскость, пересекающая шар, разбивает его на два сегмента.
Объема сегмента

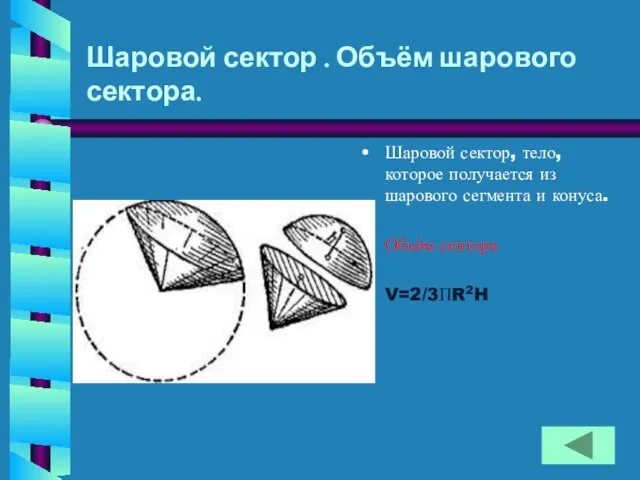
Шаровой сектор . Объём шарового сектора.
Шаровой сектор, тело, которое получается из шарового сегмента и конуса.
Объём сектора
V=2/3ПR2H

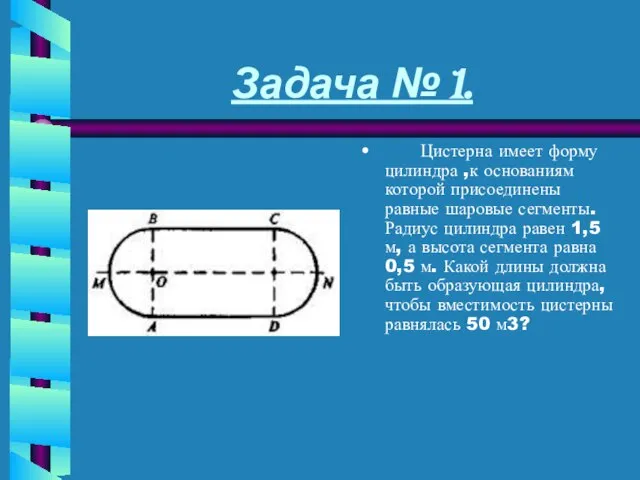
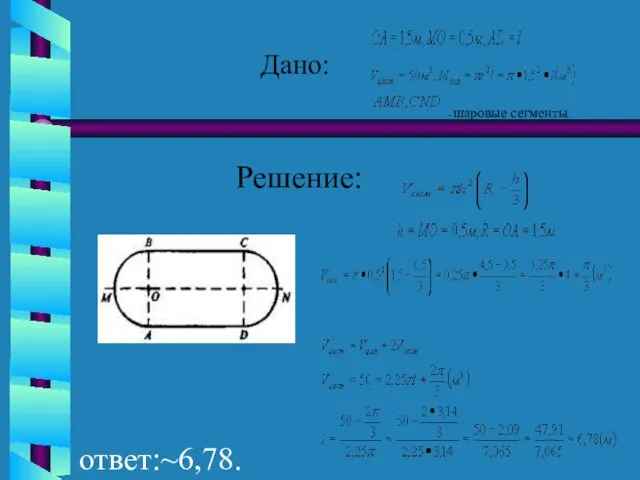
Задача № 1.
Цистерна имеет форму цилиндра ,к основаниям которой присоединены равные шаровые сегменты. Радиус цилиндра равен 1,5 м, а высота сегмента равна 0,5 м. Какой длины должна быть образующая цилиндра, чтобы вместимость цистерны равнялась 50 м3?

Дано:
.
.
- шаровые сегменты.
ответ:~6,78.
м.
Решение:

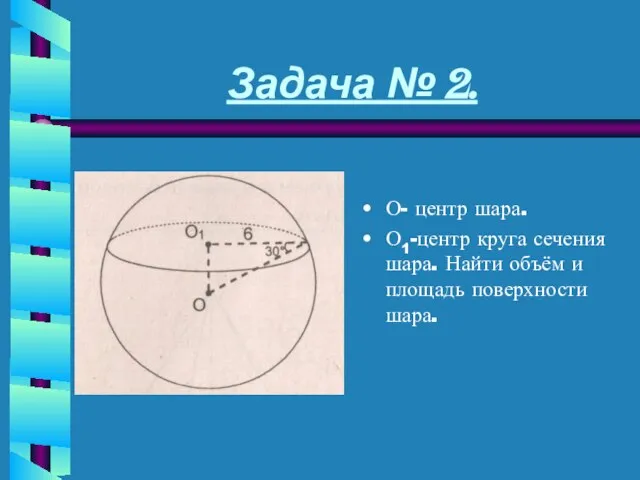
Задача № 2.
О- центр шара.
О1-центр круга сечения шара. Найти объём и площадь поверхности шара.

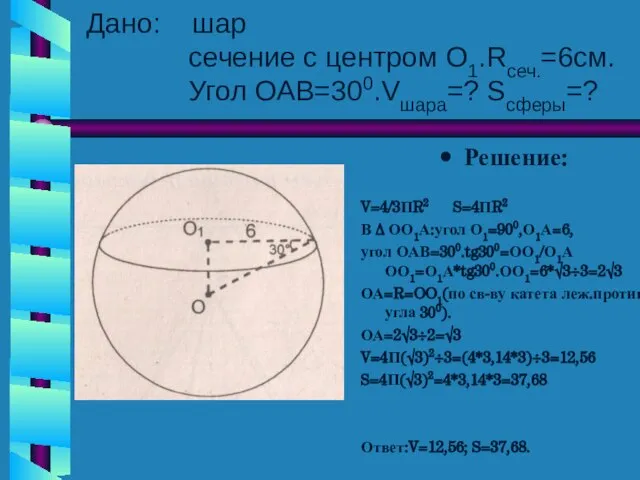
Дано: шар
сечение с центром О1.Rсеч.=6см.
Угол ОАВ=300.Vшара=? Sсферы=?
Решение:
V=4/3ПR2 S=4ПR2
В ∆ ОО1А:угол О1=900,О1А=6,
угол ОАВ=300.tg300=ОО1/О1А ОО1=О1А*tg300.ОО1=6*√3÷3=2√3
ОА=R=OO1(по св-ву катета леж.против угла 300).
ОА=2√3÷2=√3
V=4П(√3)2÷3=(4*3,14*3)÷3=12,56
S=4П(√3)2=4*3,14*3=37,68
Ответ:V=12,56; S=37,68.

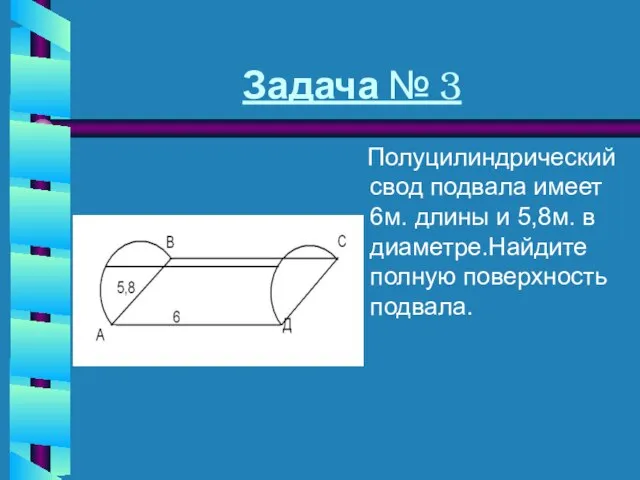
Задача № 3
Полуцилиндрический свод подвала имеет 6м. длины и 5,8м. в диаметре.Найдите полную поверхность подвала.