Содержание
- 2. ВИДЫ ДЕЛЕНИЯ ОКРУЖНОСТИ: Деление на 4 и 8 частей. Деление на 3, 6 и 12 частей.
- 3. СПИСОК ЛИТЕРАТУРЫ: http://fismat.ru/geomet/osnov/
- 4. ДЕЛЕНИЕ НА 4 И 8 ЧАСТЕЙ. Деление окружности на четыре и восемь равных частей производится в
- 6. ДЕЛЕНИЕ НА 3, 6 И 12 ЧАСТЕЙ. Деление окружности на три, шесть и двенадцать равных частей
- 8. ДЕЛЕНИЕ НА 5 И 10 ЧАСТЕЙ. Деление окружности на пять равных частей выполняется в следующей последовательности:
- 10. ДЕЛЕНИЕ НА 7 ЧАСТЕЙ. Деление окружности на семь равных частей выполняется в следующей последовательности: Из точки
- 12. Скачать презентацию
Слайд 2ВИДЫ ДЕЛЕНИЯ ОКРУЖНОСТИ:
Деление на 4 и 8 частей.
Деление на 3, 6 и
ВИДЫ ДЕЛЕНИЯ ОКРУЖНОСТИ:
Деление на 4 и 8 частей.
Деление на 3, 6 и

12 частей.
Деление на 5 и10 частей.
Деление на 7 частей.
Деление на 5 и10 частей.
Деление на 7 частей.
Слайд 3СПИСОК ЛИТЕРАТУРЫ:
http://fismat.ru/geomet/osnov/
СПИСОК ЛИТЕРАТУРЫ:
http://fismat.ru/geomet/osnov/

Слайд 4ДЕЛЕНИЕ НА 4 И 8 ЧАСТЕЙ.
Деление окружности на четыре и восемь
ДЕЛЕНИЕ НА 4 И 8 ЧАСТЕЙ.
Деление окружности на четыре и восемь

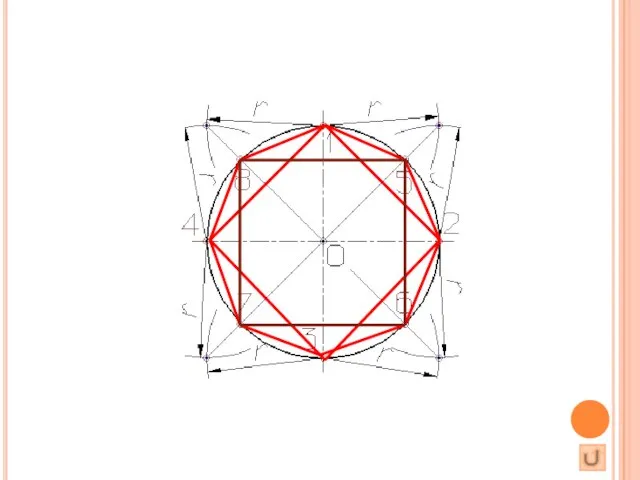
равных частей производится в следующей последовательности:
Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;
Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.
Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;
Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.
Слайд 6ДЕЛЕНИЕ НА 3, 6 И 12 ЧАСТЕЙ.
Деление окружности на три, шесть
ДЕЛЕНИЕ НА 3, 6 И 12 ЧАСТЕЙ.
Деление окружности на три, шесть

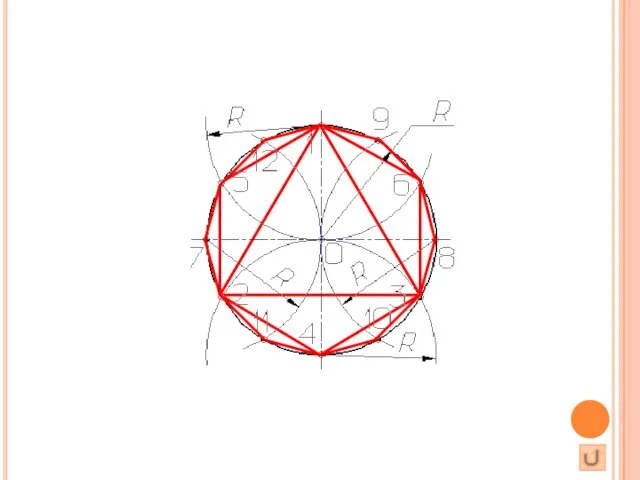
и двенадцать равных частей выполняется в следующей последовательности:
Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью
Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;
Точки 1, 2 и 3 делят окружность на три равные части;
Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;
Точки 1 - 6 делят окружность на шесть равных частей;
Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;
Точки 1 - 12 делят окружность на двенадцать равных частей.
Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью
Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;
Точки 1, 2 и 3 делят окружность на три равные части;
Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;
Точки 1 - 6 делят окружность на шесть равных частей;
Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;
Точки 1 - 12 делят окружность на двенадцать равных частей.
Слайд 8ДЕЛЕНИЕ НА 5 И 10 ЧАСТЕЙ.
Деление окружности на пять равных частей
ДЕЛЕНИЕ НА 5 И 10 ЧАСТЕЙ.
Деление окружности на пять равных частей

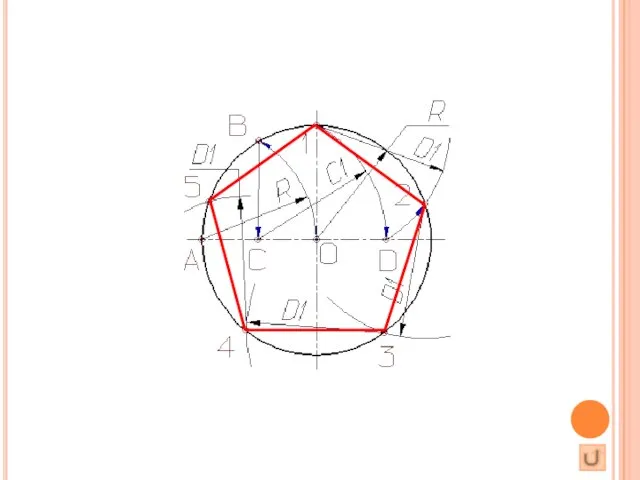
выполняется в следующей последовательности:
Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;
Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;
Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1. (+ 5 точек и получаем 10 частей)
Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;
Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;
Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1. (+ 5 точек и получаем 10 частей)
Слайд 10ДЕЛЕНИЕ НА 7 ЧАСТЕЙ.
Деление окружности на семь равных частей выполняется в
ДЕЛЕНИЕ НА 7 ЧАСТЕЙ.
Деление окружности на семь равных частей выполняется в

следующей последовательности:
Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7.
Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
Из точки В опускают перпендикуляр на горизонтальную осевую линию;
Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7.
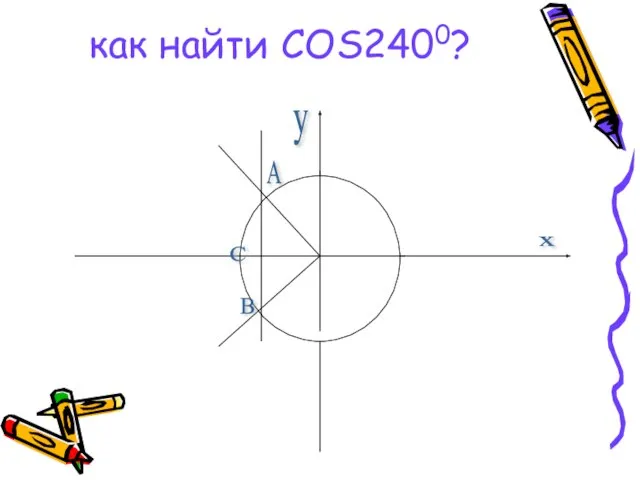 Косинус
Косинус Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Цилиндр и конус
Цилиндр и конус Преобразования на плоскости
Преобразования на плоскости ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга
ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга Правильный додекаэдр
Правильный додекаэдр Основные формулы тригонометрии
Основные формулы тригонометрии Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Векторы 9 класс
Векторы 9 класс В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ вид разреза сечения
вид разреза сечения Окружность в аксонометрии
Окружность в аксонометрии Параллельность в пространстве
Параллельность в пространстве Биссектриса угла
Биссектриса угла Правильные многогранники
Правильные многогранники Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Площади и объемы - презентация по Геометрии_
Площади и объемы - презентация по Геометрии_ Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Приготовьтесь к построению
Приготовьтесь к построению План –конспект урока. Тема: «Треугольник» 5 класс.
План –конспект урока. Тема: «Треугольник» 5 класс. ЭЛЛИПС
ЭЛЛИПС Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Сумма двух векторов Геометрия -9 Урок 4
Сумма двух векторов Геометрия -9 Урок 4 Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Почему квадрат?
Почему квадрат? Теорема синусов 9 класс
Теорема синусов 9 класс Свойство и признак описанного четырёхугольника
Свойство и признак описанного четырёхугольника Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_