Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Содержание
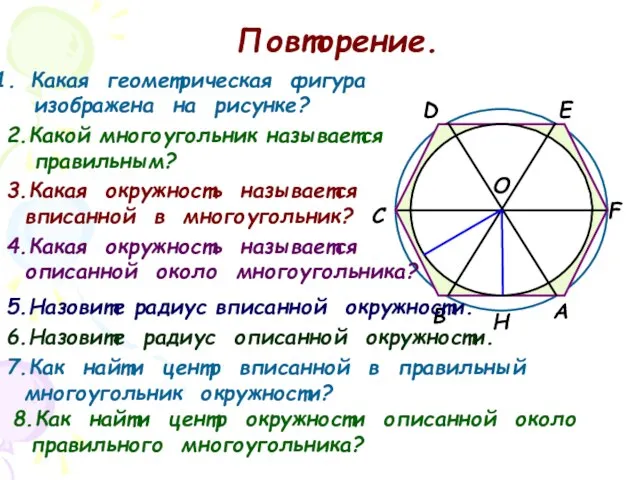
- 2. А В С D Е F О Н Повторение. Какая геометрическая фигура изображена на рисунке? 3.Какая
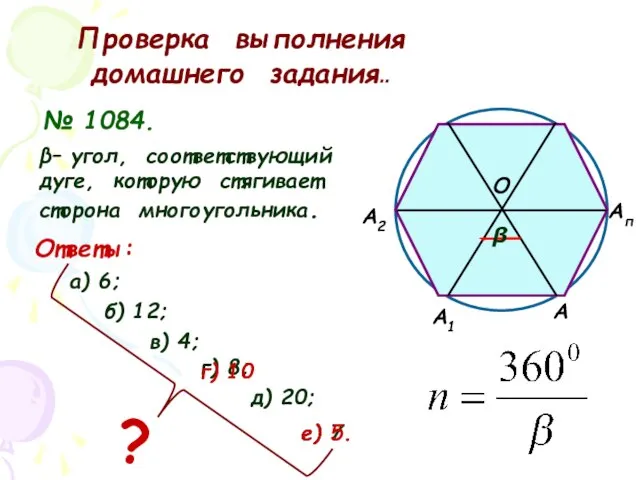
- 3. А А1 А2 Ап О Проверка выполнения домашнего задания.. № 1084. β– угол, соответствующий дуге, которую
- 4. Т – тест. Задание на карточках. Работу выполнить на листочках. Время выполнения ограничено. Критерии оценки: «5»
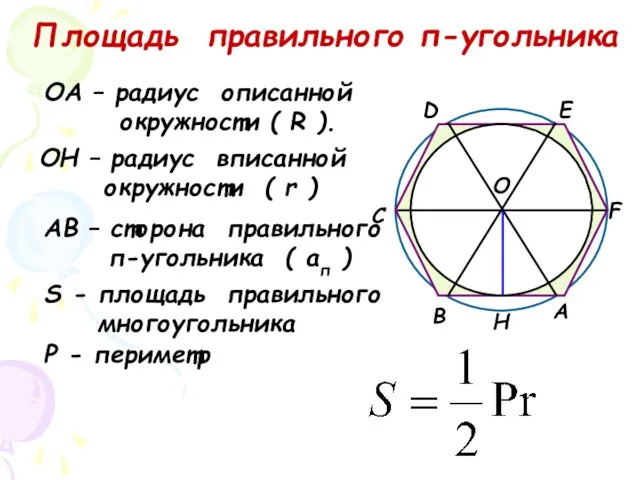
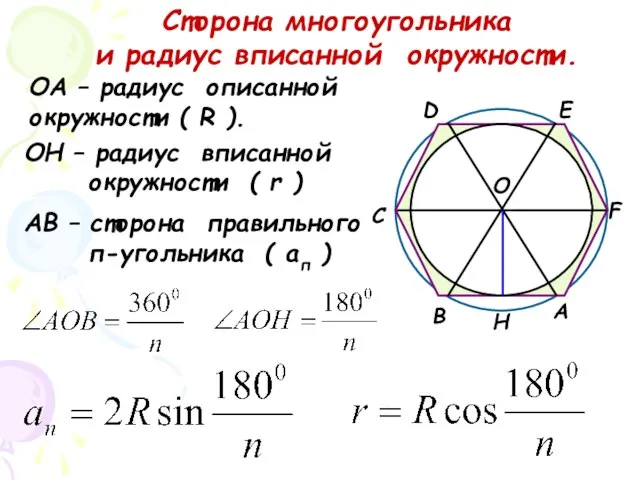
- 5. А В С D Е F О Н ОА – радиус описанной окружности ( R ).
- 6. А В С D Е F О Н ОА – радиус описанной окружности ( R ).
- 7. п = 3 п = 4 п = 6
- 8. Домашнее задание: Пп. 105 – 108; № 1087; № 1088 – подготовить таблицу.
- 10. Скачать презентацию

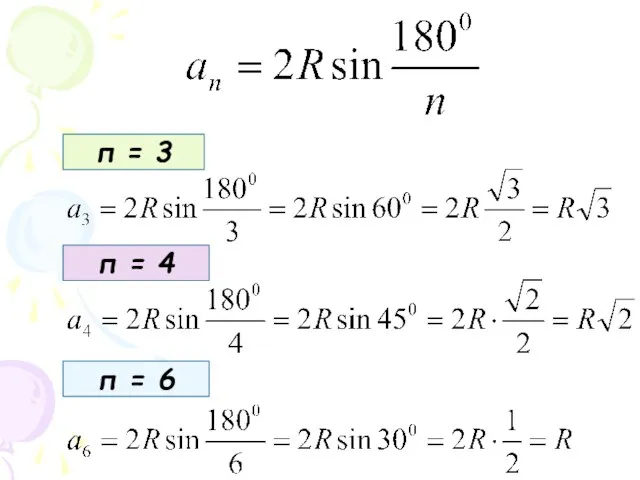

 Флексагоны флексоры
Флексагоны флексоры Многогранник
Многогранник Пирамиды
Пирамиды Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Площади
Площади Геометрия.Введение. Аксиоматика.
Геометрия.Введение. Аксиоматика. Периметр – сумма длин всех сторон.
Периметр – сумма длин всех сторон. Упражнения со спичками (занятие 9)
Упражнения со спичками (занятие 9) Пирамида, вписанная в конус
Пирамида, вписанная в конус Стереометрия в образах
Стереометрия в образах Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Понятие цилиндра
Понятие цилиндра Четыре замечательные точки треугольника
Четыре замечательные точки треугольника ГИА 2013 Модуль «Геометрия» № 11
ГИА 2013 Модуль «Геометрия» № 11 Презентация на тему: Тела Платона
Презентация на тему: Тела Платона Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ Магические квадраты
Магические квадраты Четырехугольники
Четырехугольники Мир многогранников
Мир многогранников Симметрия на планете Земля
Симметрия на планете Земля Перпендикулярные прямые 7 класс
Перпендикулярные прямые 7 класс Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Правильный додекаэдр
Правильный додекаэдр Вписанные углы
Вписанные углы Теоремы синусов и косинусов
Теоремы синусов и косинусов Лист Мёбиуса
Лист Мёбиуса Лобачевский - «Коперник геометрии»
Лобачевский - «Коперник геометрии»