Содержание
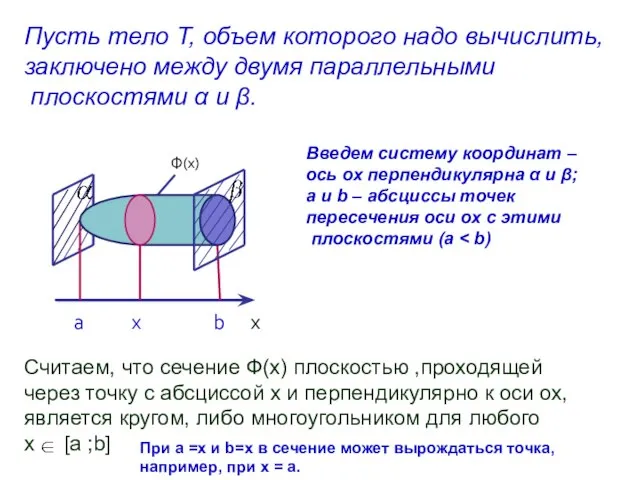
- 2. Пусть тело Т, объем которого надо вычислить, заключено между двумя параллельными плоскостями α и β. Введем
- 3. Ф(х1) Ф(х2) Ф(хi) Ф(хn) хо=а х1 х2 хi-1 хi x n=b Пусть S(x) - площадь Ф(х).
- 4. И в том , и в другом случае объем тела Тi приближенно равен Vn = S(xi)Δxi
- 5. В классе: № 673, № 674 № 674
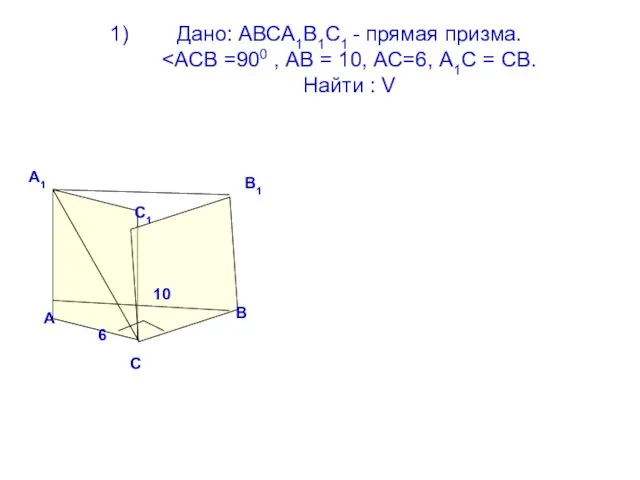
- 6. Дано: АВСА1В1С1 - прямая призма. А С В 6 10 А1 С1 В1
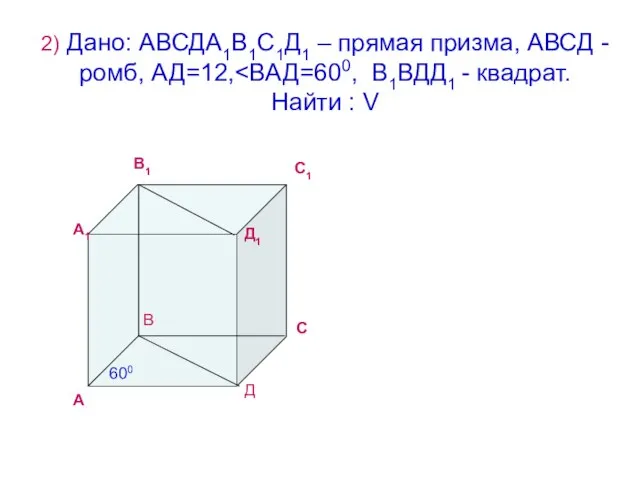
- 7. 2) Дано: АВСДА1В1С1Д1 – прямая призма, АВСД - ромб, АД=12, А В С Д А1 В1
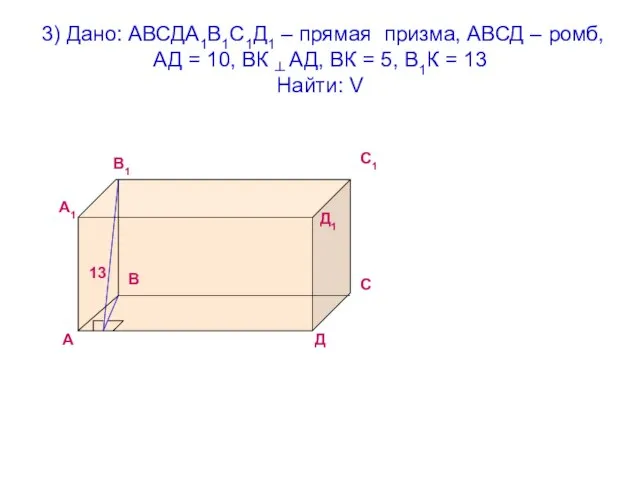
- 8. 3) Дано: АВСДА1В1С1Д1 – прямая призма, АВСД – ромб, АД = 10, ВК ┴ АД, ВК
- 10. Скачать презентацию



 Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Сечения
Сечения Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Призма 9 класс
Призма 9 класс Окружность и круг
Окружность и круг Объем конуса цилиндра
Объем конуса цилиндра Параллелограмм
Параллелограмм Параллельность в пространстве
Параллельность в пространстве Перпендикулярные прямые на плоскости
Перпендикулярные прямые на плоскости Сумма углов треугольника 7 класс
Сумма углов треугольника 7 класс Сумма углов треугольника
Сумма углов треугольника Секреты квадрата и кубика
Секреты квадрата и кубика Решение треугольников. Измерительные работы на местности. Тема урока:
Решение треугольников. Измерительные работы на местности. Тема урока: Развитие пространственного мышления
Развитие пространственного мышления Графический способ решения систем укравнений
Графический способ решения систем укравнений Вводное повторение курса геометрии
Вводное повторение курса геометрии Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Осевая и центральная симметрии
Осевая и центральная симметрии Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Шар, вписанный в пирамиду, призму, конус
Шар, вписанный в пирамиду, призму, конус Многогранник
Многогранник Бозон Хиддинса
Бозон Хиддинса Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии
Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии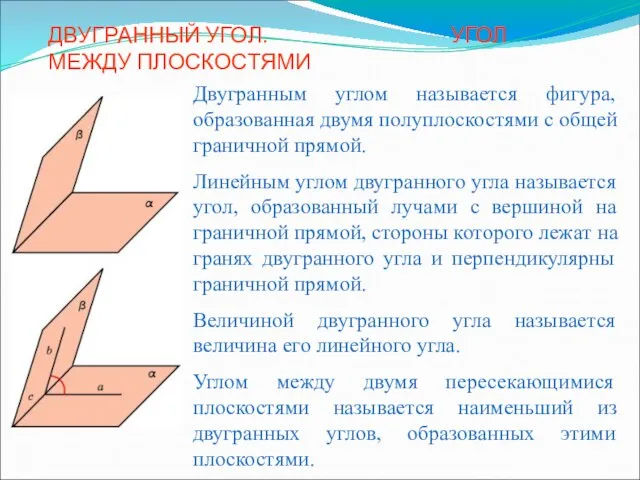 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Смотр общественных знаний
Смотр общественных знаний Уравнение прямой в пространстве
Уравнение прямой в пространстве Параллельные прямые 6 класс
Параллельные прямые 6 класс