Содержание
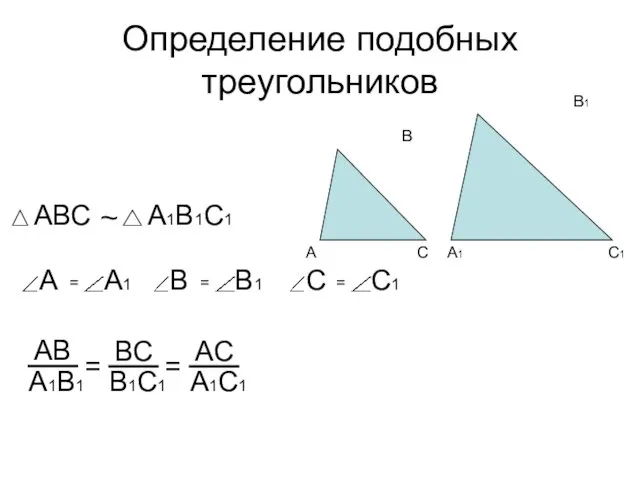
- 2. Определение подобных треугольников ~ = =
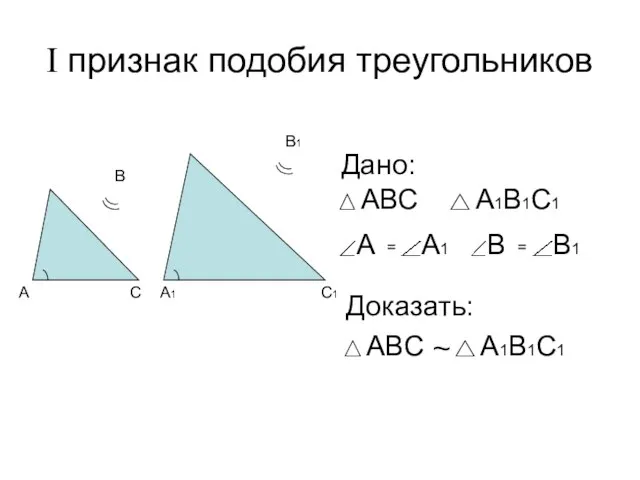
- 3. I признак подобия треугольников Дано: Доказать: ~
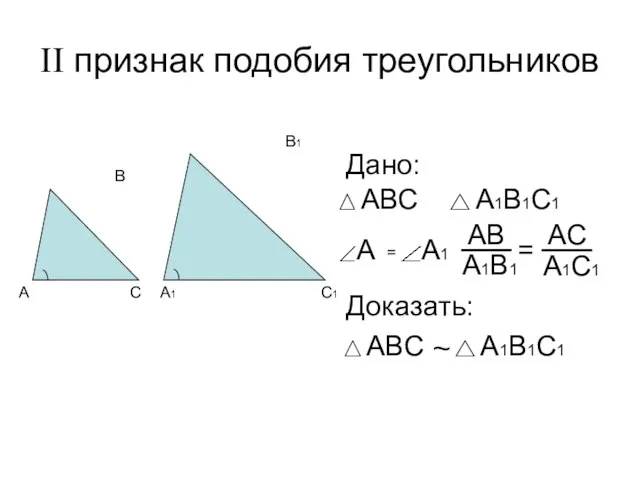
- 4. II признак подобия треугольников Дано: Доказать: = ~
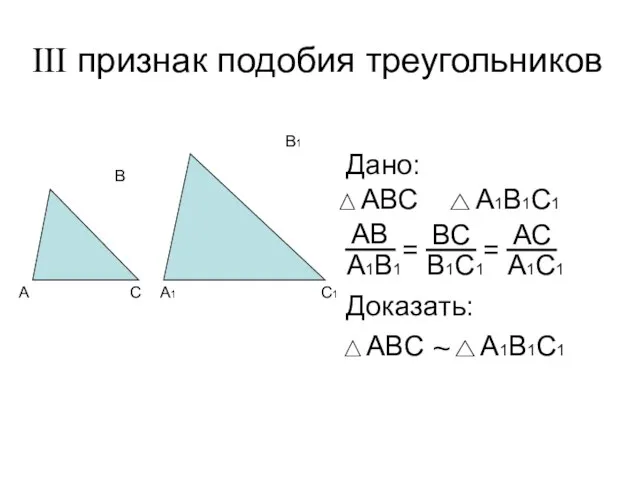
- 5. III признак подобия треугольников Дано: Доказать: ~ = =
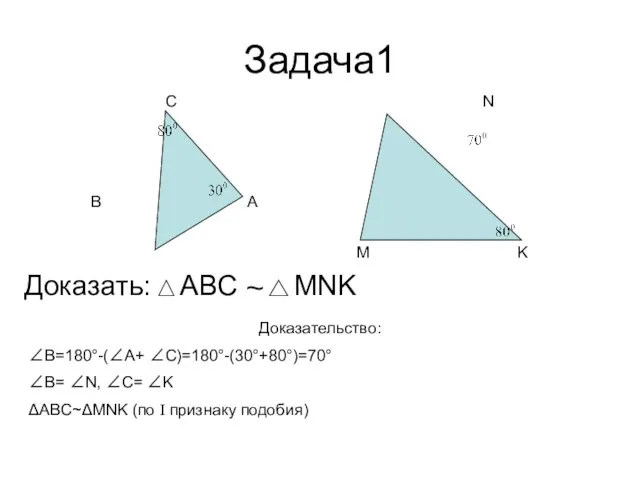
- 6. Задача1 А В С Доказать: ~ Доказательство: ∠В=180°-(∠А+ ∠С)=180°-(30°+80°)=70° ∠В= ∠N, ∠C= ∠K ΔABC~ΔMNK (по I
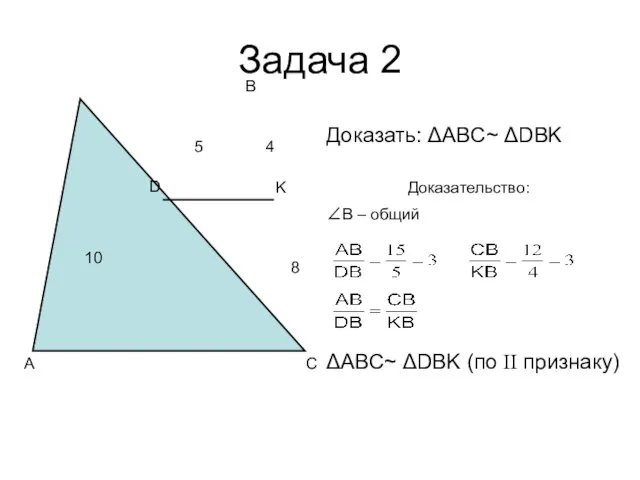
- 7. Задача 2 A B C D K 4 8 10 5 Доказать: ΔABC~ ΔDBK Доказательство: ∠B
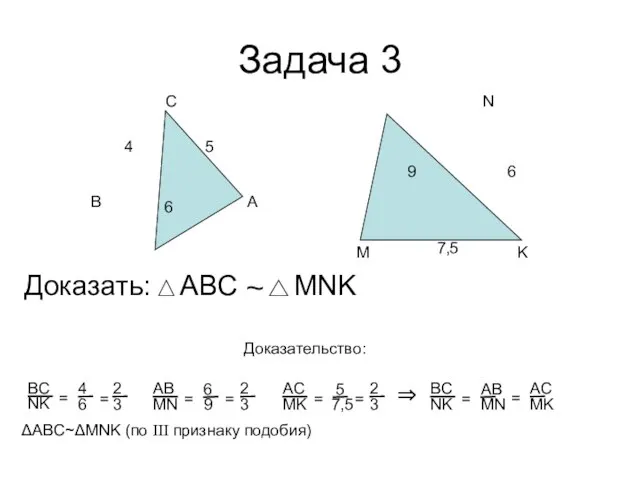
- 8. Задача 3 А В С Доказать: ~ Доказательство: ΔABC~ΔMNK (по III признаку подобия) 4 5 6
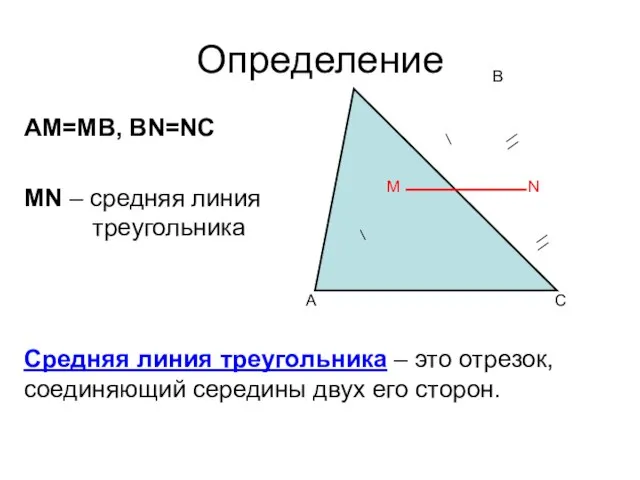
- 9. Определение A C B M N AM=MB, BN=NC MN – средняя линия треугольника Средняя линия треугольника
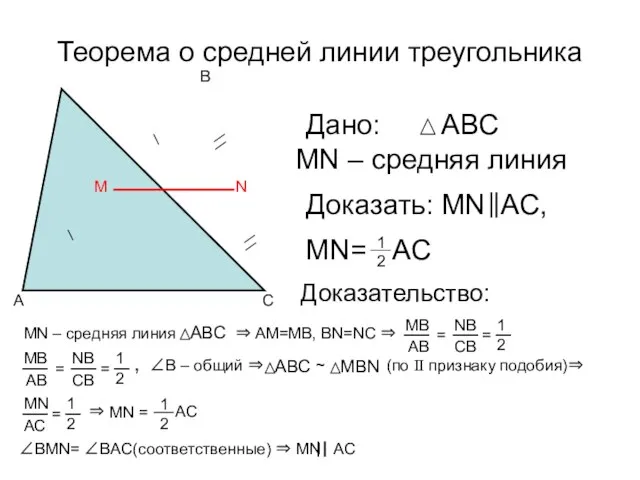
- 10. Теорема о средней линии треугольника Дано: MN – средняя линия Доказать: MN AC, MN= 1 2
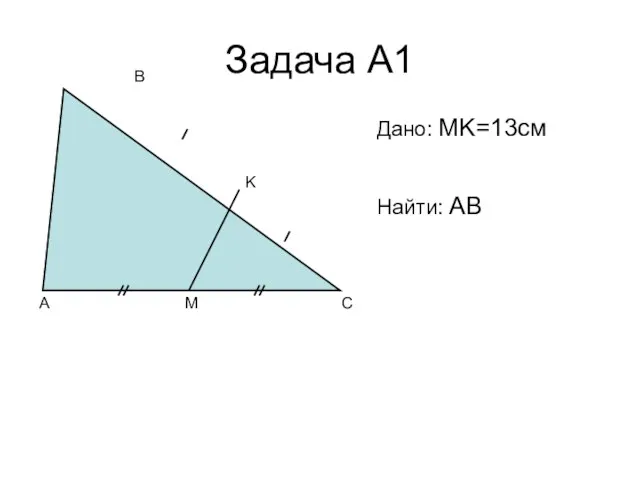
- 11. Задача А1 A C B M K Дано: MK=13см Найти: AB
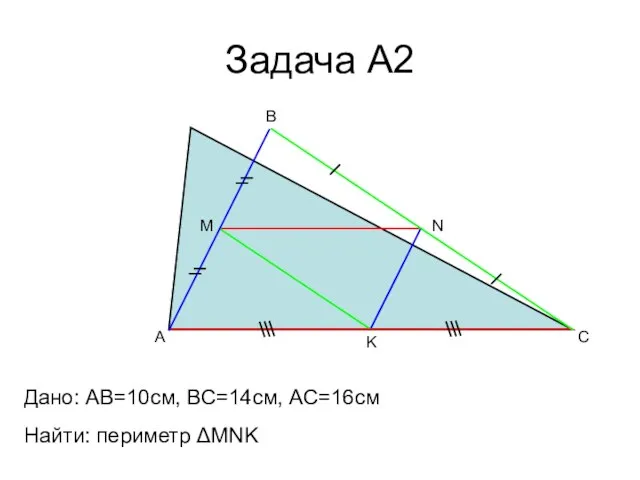
- 12. Задача А2 A B C M N K Дано: AB=10cм, ВС=14см, АС=16см Найти: периметр ΔMNK
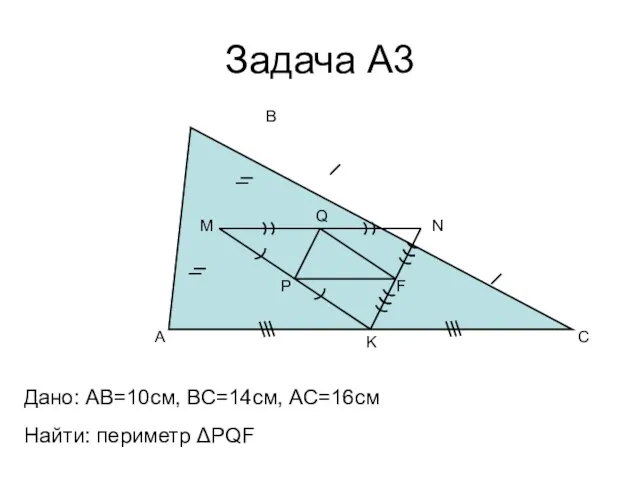
- 13. Задача А3 A B C M N K P Q F Дано: AB=10cм, ВС=14см, АС=16см Найти:
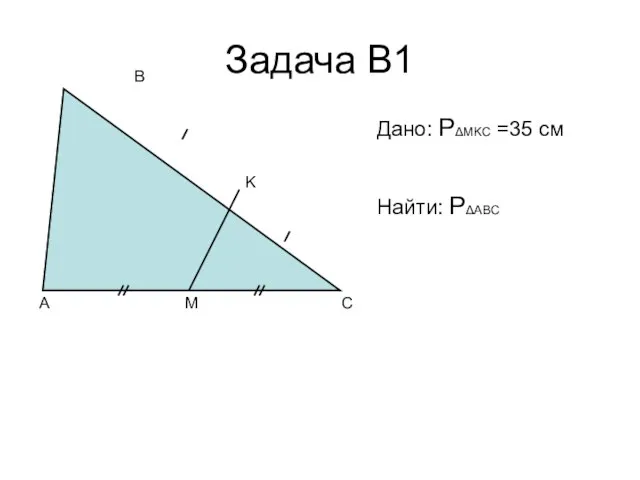
- 14. Задача В1 A C B M K Дано: PΔMKC =35 см Найти: PΔABC
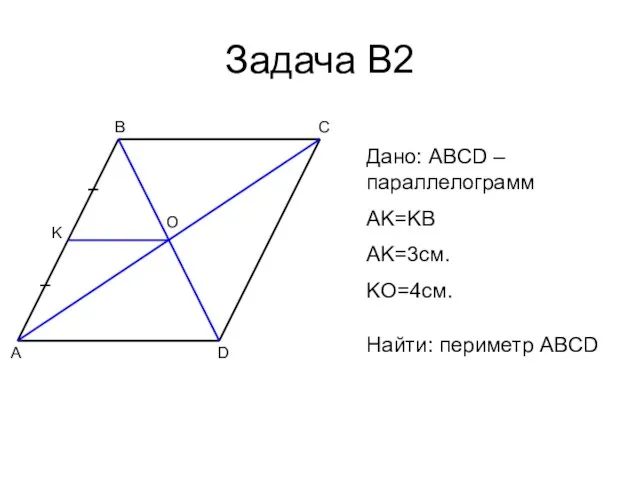
- 15. Задача В2 A B C D O K Дано: ABCD – параллелограмм AK=KB AK=3см. KO=4см. Найти:
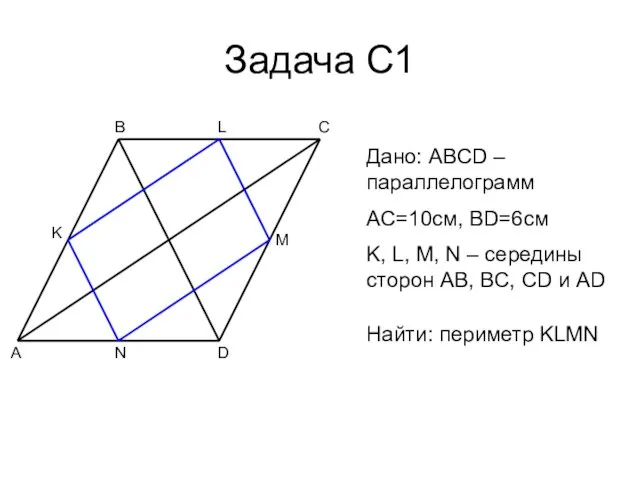
- 16. Задача С1 A B C D M N K Дано: ABCD – параллелограмм AC=10см, BD=6см K,
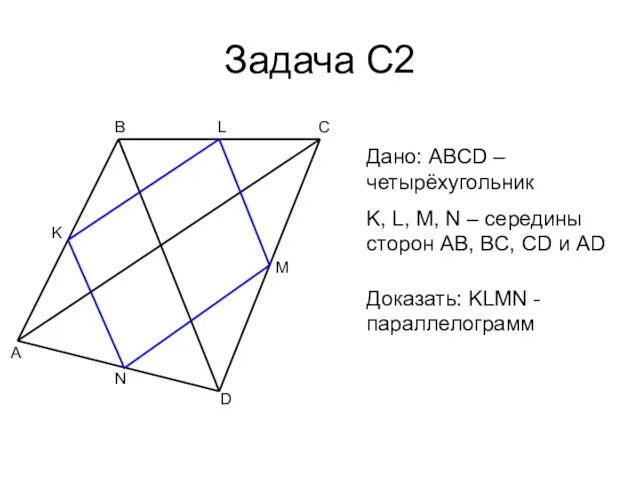
- 17. Задача С2 A B C D M N K Дано: ABCD – четырёхугольник K, L, M,
- 18. Вариньон Пьер (1654-1722)
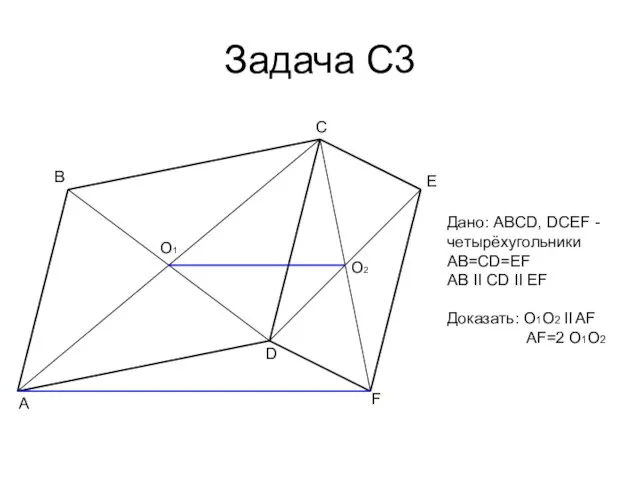
- 19. Задача С3 A B C D E F O1 O2 Дано: ABCD, DCEF - четырёхугольники AB=CD=EF
- 21. Скачать презентацию

 Правильные выпуклые многогранники
Правильные выпуклые многогранники Признаки равенства треугольников 7 класс
Признаки равенства треугольников 7 класс Карточки - задания по теме "Конус"
Карточки - задания по теме "Конус"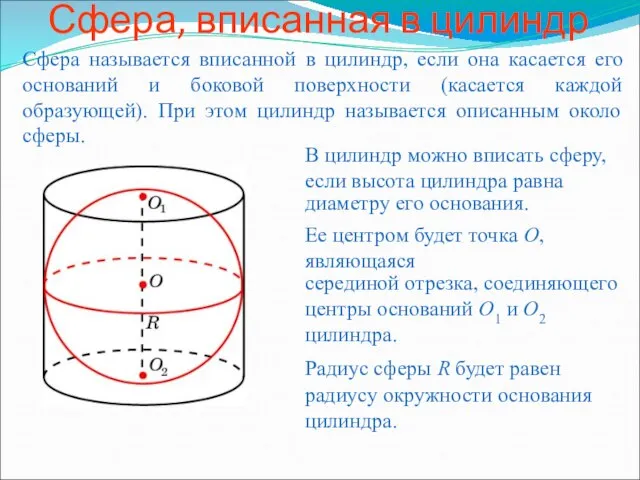 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Скрещивающиеся прямые
Скрещивающиеся прямые Координаты вектора
Координаты вектора ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности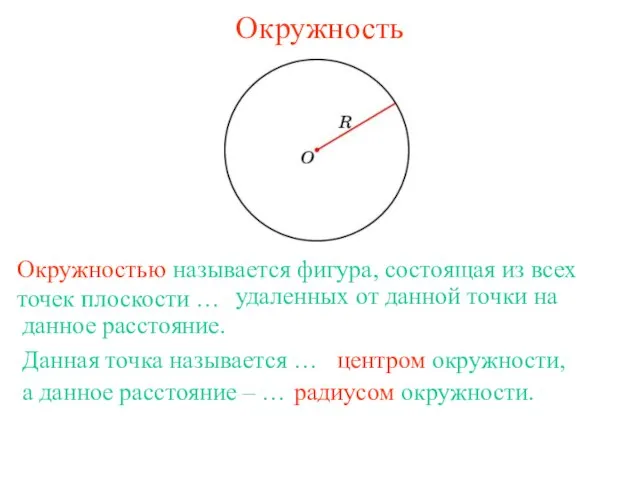 Окружность
Окружность Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Круг и окружность
Круг и окружность Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Чертёж группы геометрических тел.
Чертёж группы геометрических тел. Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Преобразование плоскости
Преобразование плоскости Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Логарифм. Основные понятия
Логарифм. Основные понятия ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Площади (8 класс)
Площади (8 класс) Площади фигур. Зачёт
Площади фигур. Зачёт Геометрия в жизни
Геометрия в жизни Музей истории четырёхугольников
Музей истории четырёхугольников В мире треугольников
В мире треугольников Знакомство с миром геометрии
Знакомство с миром геометрии Смежные и вертикальные углы
Смежные и вертикальные углы