Содержание
- 2. Определение и признак параллельности прямой и плоскости Постройте плоскость, параллельную данной прямой и проходящую через а)
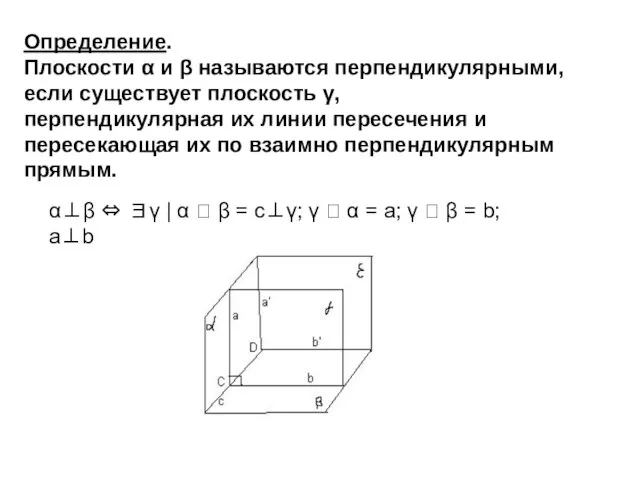
- 3. Определение. Плоскости α и β называются перпендикулярными, если существует плоскость γ, перпендикулярная их линии пересечения и
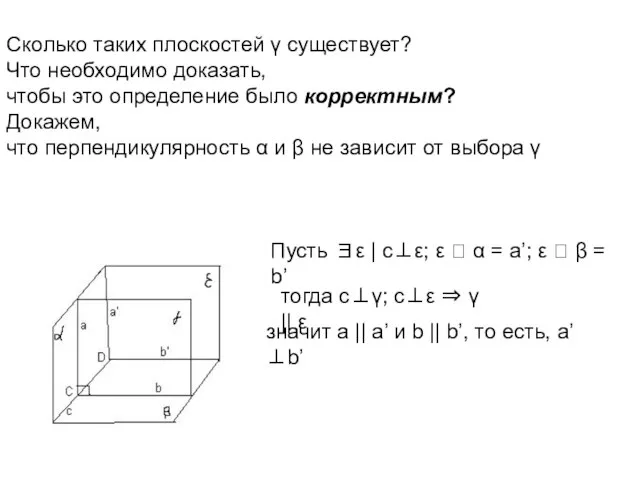
- 4. Сколько таких плоскостей γ существует? Что необходимо доказать, чтобы это определение было корректным? Докажем, что перпендикулярность
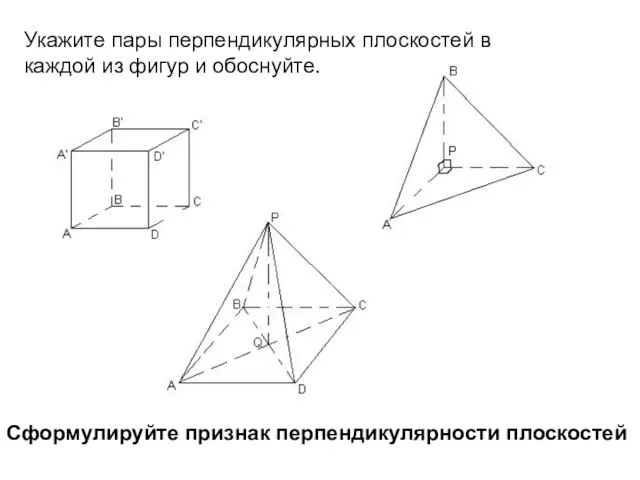
- 5. Укажите пары перпендикулярных плоскостей в каждой из фигур и обоснуйте. Сформулируйте признак перпендикулярности плоскостей
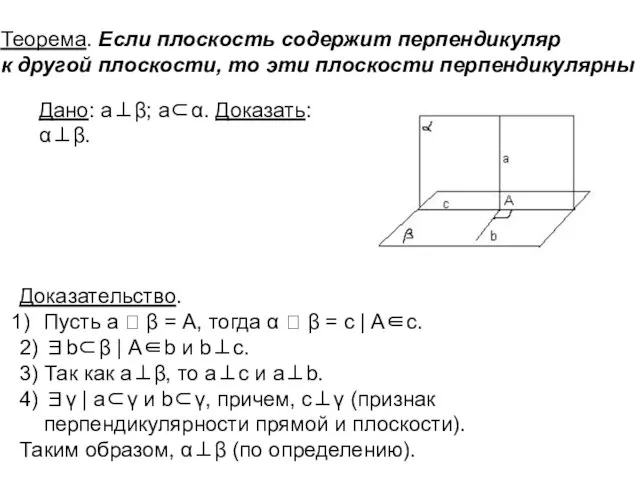
- 6. . Теорема. Если плоскость содержит перпендикуляр к другой плоскости, то эти плоскости перпендикулярны Доказательство. Пусть а
- 8. Скачать презентацию

 Сумма углов треугольника 5 класс - презентация_
Сумма углов треугольника 5 класс - презентация_ Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Графический способ решения систем укравнений
Графический способ решения систем укравнений Измерение объема тела
Измерение объема тела Двугранные углы
Двугранные углы Понятие движения
Понятие движения Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья
Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья  Параллелипипед
Параллелипипед Тетраэдр
Тетраэдр Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья
Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья Части фигур
Части фигур Правила нанесения размеров на чертежах
Правила нанесения размеров на чертежах Вневписанная окружность
Вневписанная окружность Плоскость
Плоскость Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Треугольник Устные задачи
Треугольник Устные задачи Анализ геометрической формы предмета
Анализ геометрической формы предмета Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Презентация на тему: Параллельный перенос
Презентация на тему: Параллельный перенос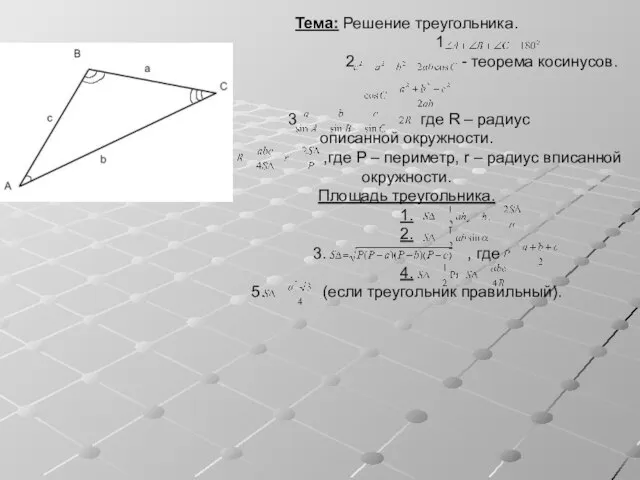 Решение треугольника
Решение треугольника Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Смотр общественных знаний
Смотр общественных знаний Цилиндр и конус
Цилиндр и конус Площадь трапеции
Площадь трапеции Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач