Содержание
- 2. Цели и задачи: Познакомиться с понятием “граф”, с его основными элементами: вершина, ребра. Научиться составлять графы
- 3. Введение Впервые с задачами, для решения которых используются графы, мы встретились на олимпиаде по математике. Трудности
- 5. Немного из истории Л. Эйлер (1707-1782, российский математик, швейцарец по происхождению, академик Петербургской и Берлинской академии
- 6. Понятие графов В математике графом называют набор точек некоторые из которых соединены линиями. Точки именуются вершинами
- 7. «В математике следует помнить не формулы, а процесс мышления» Е. И. Игнатьева
- 8. 1. Знаете ли Вы, что такое «ГРАФЫ»? 2. Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече
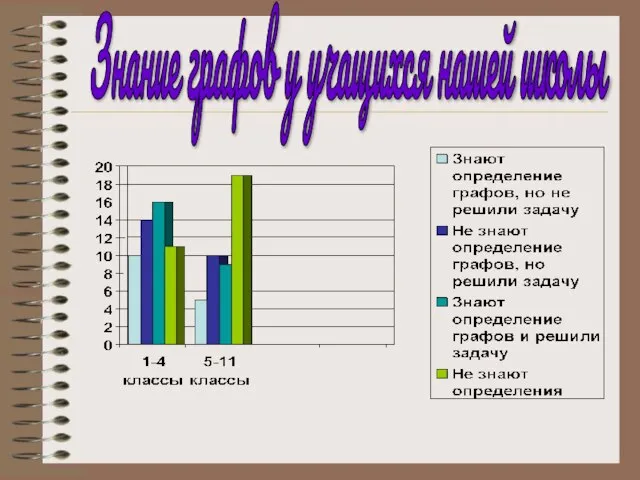
- 9. Знание графов у учащихся нашей школы
- 10. Задача о Кёнигсбергских мостах Бывший Кёнигсберг(ныне Калининград)расположен на реке Прегель. В пределах города река омывает 2
- 11. Я здесь уже был!
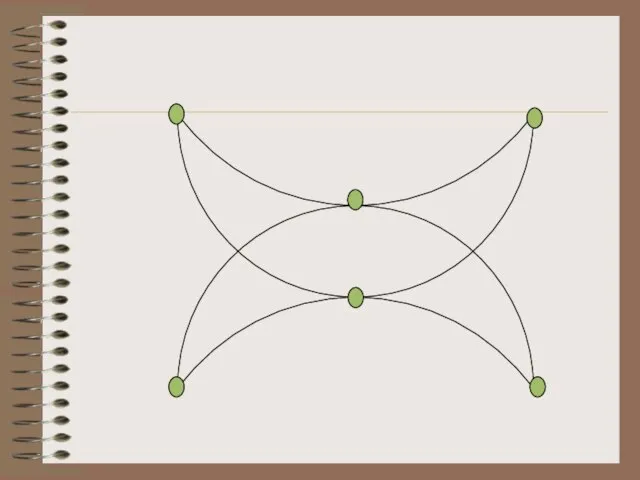
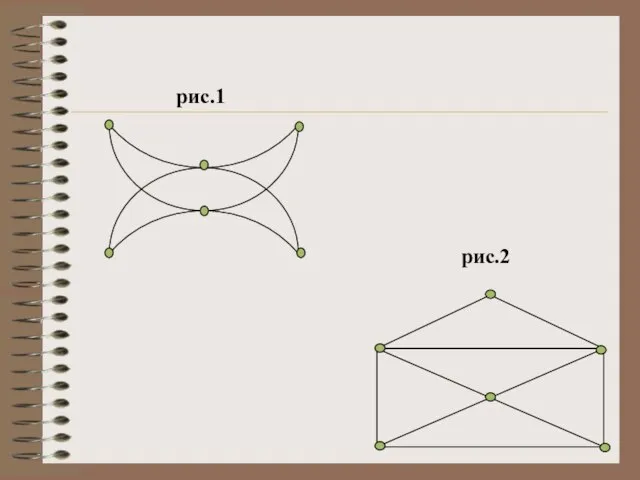
- 13. рис.2 рис.1
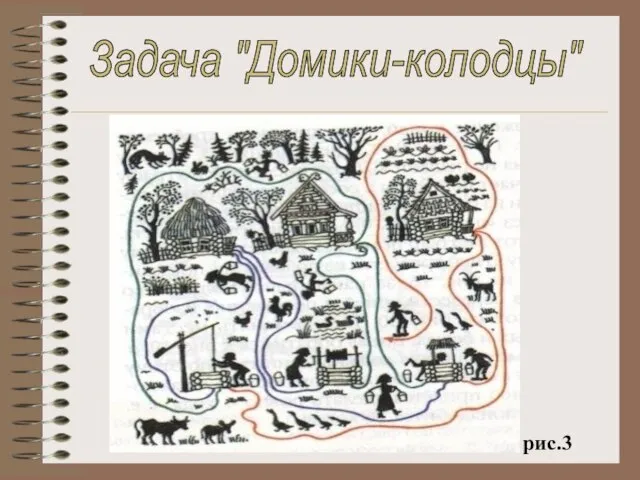
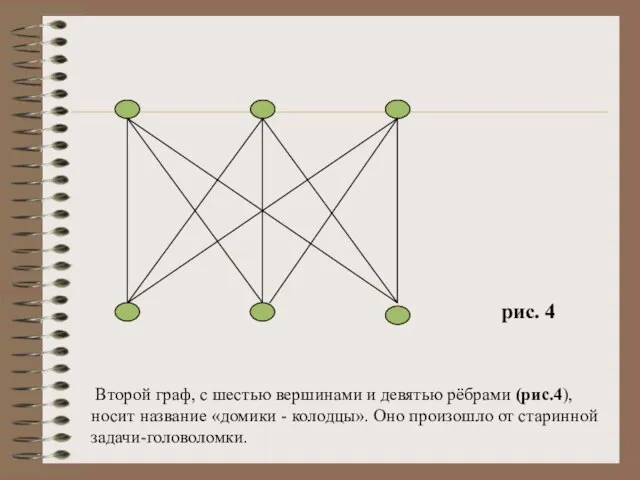
- 14. рис.3 Задача "Домики-колодцы"
- 15. Второй граф, с шестью вершинами и девятью рёбрами (рис.4), носит название «домики - колодцы». Оно произошло
- 16. Графы обладают многими интересными свойствами. Так, Эйлер обнаружил простую связь между количеством вершин (B), количеством рёбер
- 17. Если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2
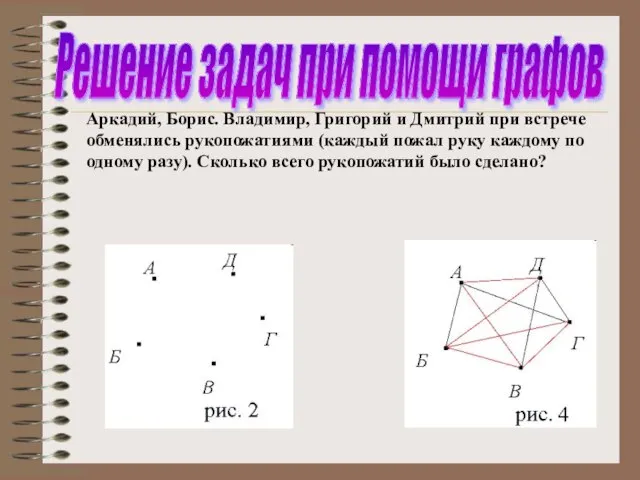
- 18. Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному
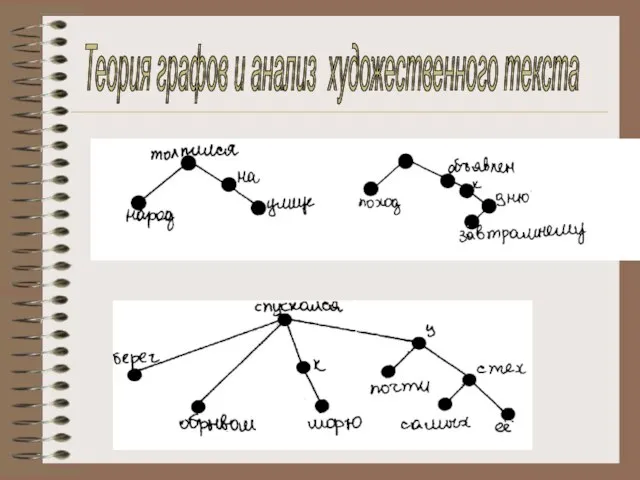
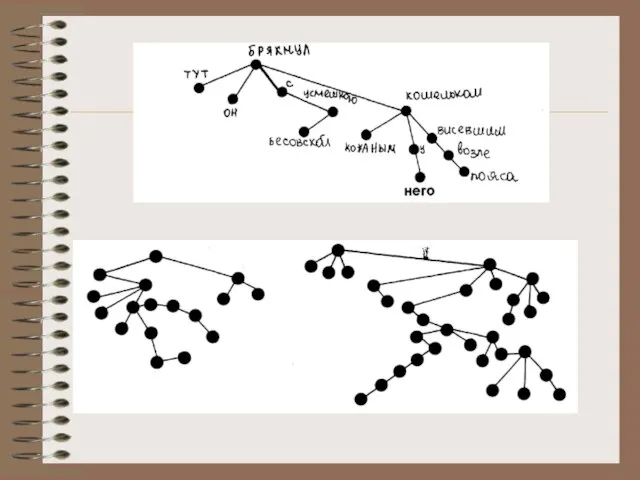
- 20. Теория графов и анализ художественного текста
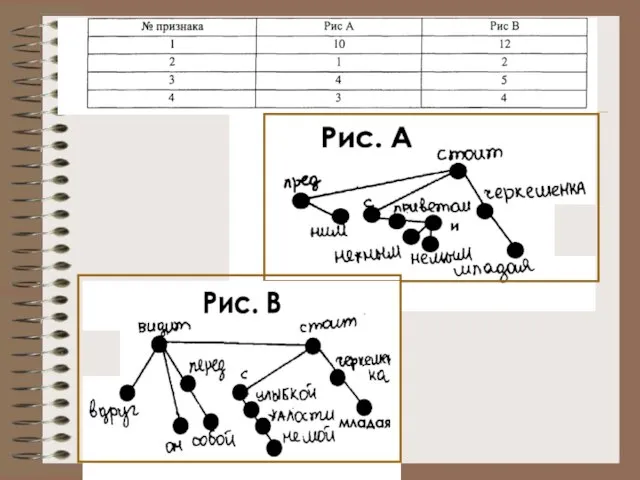
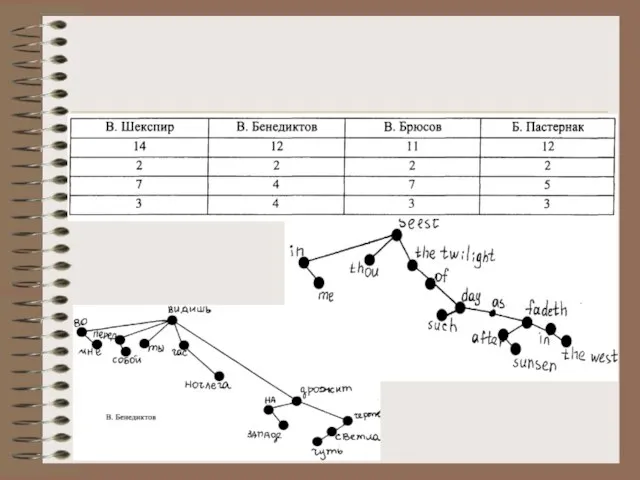
- 22. Количество узлов дерева (т.е. количество слов во фразе) Количество простых предложений в сложном (помечание стрелок, соответствующих
- 24. 1. В. Шекспир. That time of year thou mayst in me be hold When yellow leaves,
- 25. 3. В. Брюсов. То время года видишь ты во мне, Когда, желтея, листья стали редки, И
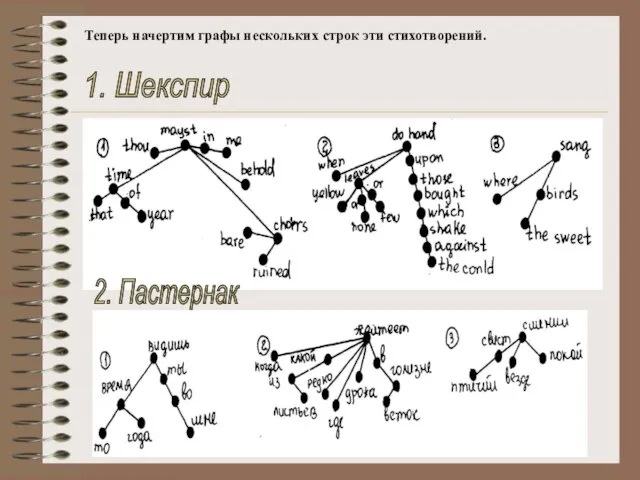
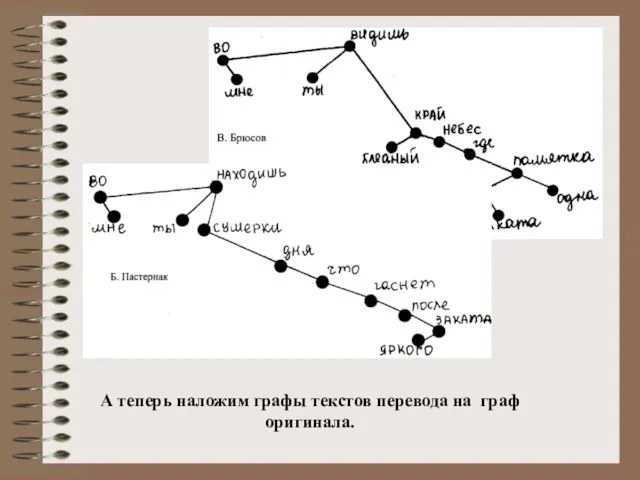
- 26. Теперь начертим графы нескольких строк эти стихотворений. 1. Шекспир 2. Пастернак
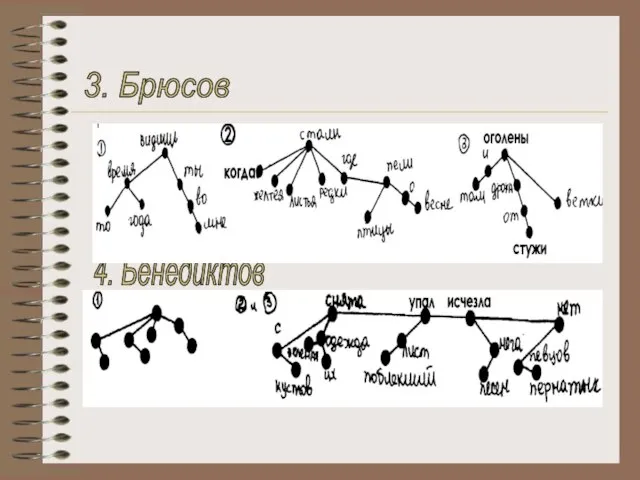
- 27. 3. Брюсов 4. Бенедиктов
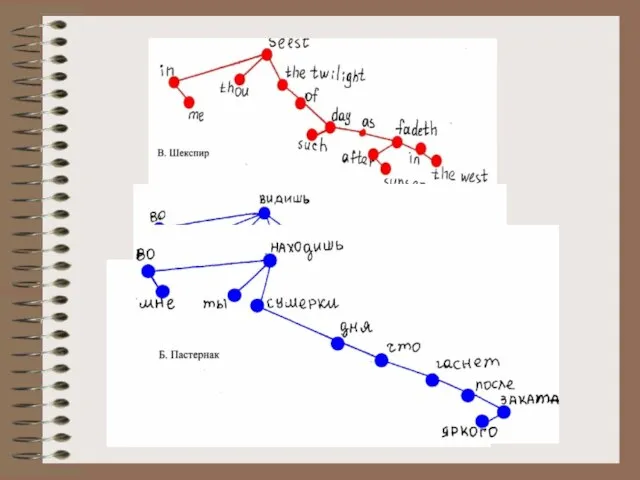
- 29. А теперь наложим графы текстов перевода на граф оригинала.
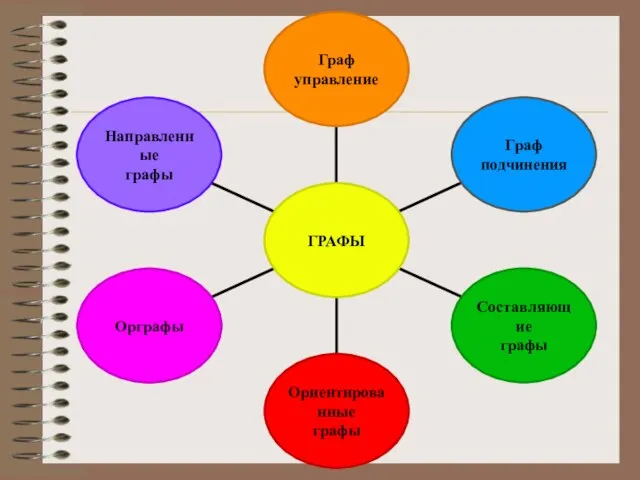
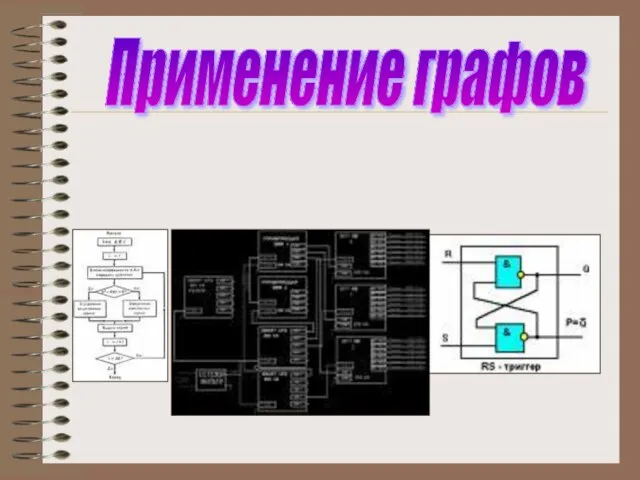
- 31. Применение графов
- 32. Применение графов
- 33. Применение графов
- 34. Применение графов
- 35. Применение графов
- 36. Применение графов
- 37. Применение графов
- 38. Применение графов
- 39. Применение графов
- 40. Эссе: Наши исследования ещё раз доказали, что всё в нашей жизни, а значит и в изучении
- 41. Заключение Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не
- 43. Скачать презентацию





















 Площадь параллелограмма 9 класс
Площадь параллелограмма 9 класс Неевклидова геометрия
Неевклидова геометрия Луч и угол (7 класс)
Луч и угол (7 класс) Длина окружности
Длина окружности Свойства пирамиды с равными боковыми ребрами
Свойства пирамиды с равными боковыми ребрами Прямоугольные треугольники 7 класс
Прямоугольные треугольники 7 класс Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:
Задачи на готовых чертежах Четырехугольники Презентацию подготовила Команда «ЗВЕЗДОЧКИ» МКУО Тумановская СОШ Руководитель:  Задачи на готовых чертежах
Задачи на готовых чертежах Теорема о вписанном угле 8 класс - презентация_
Теорема о вписанном угле 8 класс - презентация_ Скалярное произведение векторов
Скалярное произведение векторов Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Вписанные углы
Вписанные углы Преобразование плоскости
Преобразование плоскости Геометрия 10 класс - презентация по Геометрии
Геометрия 10 класс - презентация по Геометрии Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса Геометрический Конструктор «танграм»
Геометрический Конструктор «танграм» Скрещивающиеся прямые
Скрещивающиеся прямые Круг и окружность
Круг и окружность Координаты вектора
Координаты вектора ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Правильные выпуклые многогранники
Правильные выпуклые многогранники Многогранники и кристаллы
Многогранники и кристаллы Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Осевая симметрия (6 класс)
Осевая симметрия (6 класс) Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Признаки равенства и подобия треугольников
Признаки равенства и подобия треугольников