Содержание
- 2. Двумерные многообразия Пусть и – два множества в евклидовом пространстве произвольной размерности. Если задано отображение ,
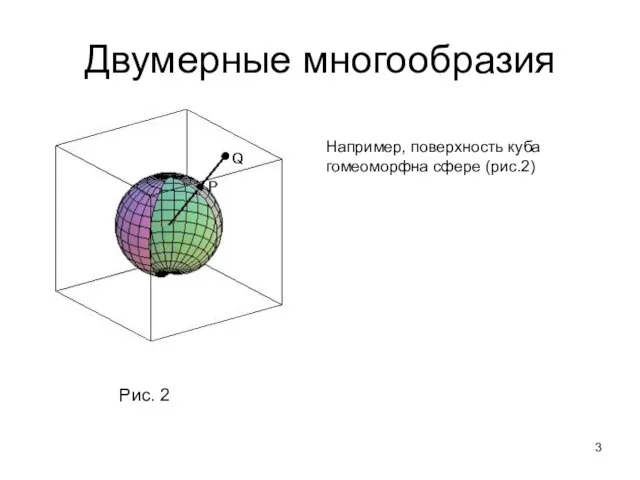
- 3. Двумерные многообразия Например, поверхность куба гомеоморфна сфере (рис.2) Рис. 2
- 4. Двумерные многообразия Рис. 3
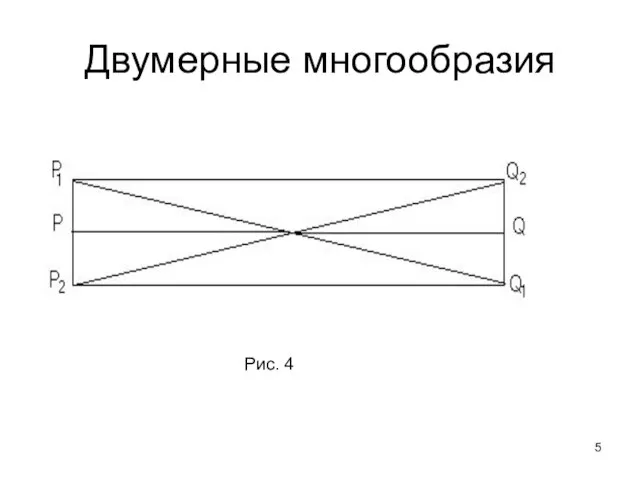
- 5. Двумерные многообразия Рис. 4
- 6. Двумерные многообразия Рис. 5
- 7. Двумерные многообразия Любая компактная двумерная поверхность гомеоморфна либо сфере с p ручками, либо сфере с q
- 8. Двумерные многообразия Рис. 7
- 9. Двумерные многообразия Рис.8
- 10. Двумерные многообразия Рис.9
- 11. Двумерные многообразия Рис. 10
- 12. Фундаментальная группа Рис. 11 Две петли и , проходящие через фиксированную точку P , называются гомотопными,
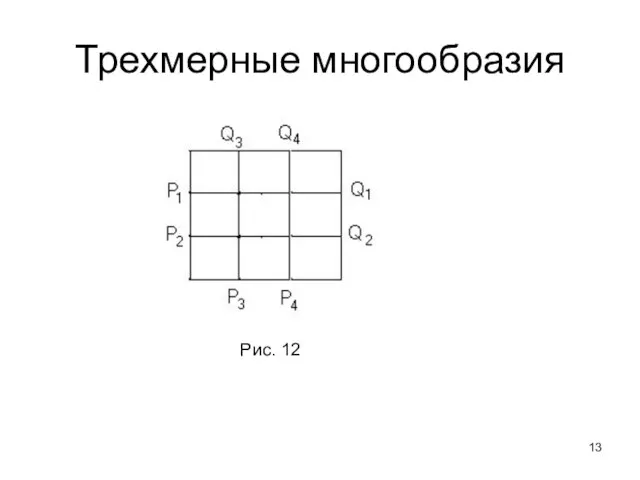
- 13. Трехмерные многообразия Рис. 12
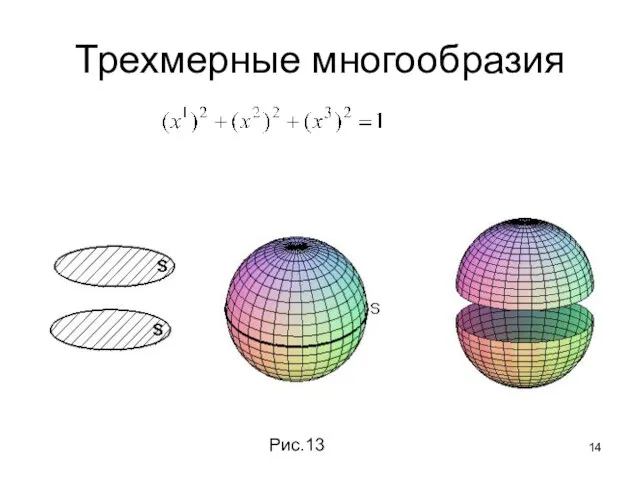
- 14. Трехмерные многообразия Рис.13
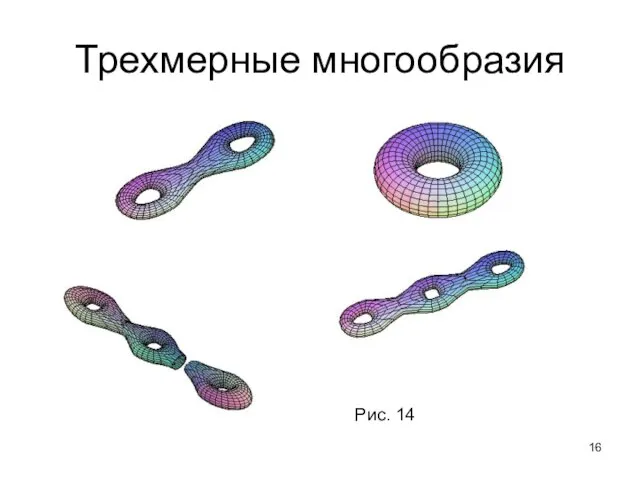
- 15. Трехмерные многообразия Каждое компактное ориентируемое 3-мерное многообразие раскладывается в связную сумму где сомножители - замкнутые неприводимые
- 16. Трехмерные многообразия Рис. 14
- 17. Трехмерные многообразия Любое трехмерное компактное неприводимое многообразие можно разрезать конечным числом несжимающихся торов на компактные многообразия,
- 18. Однородные трехмерные геометрии В трехмерном случае всего 8 стандартных геометрий, которые 1) в окрестности каждой точки
- 19. Однородные трехмерные геометрии Метрики прямого произведения: 4) ; 5) ; Возьмем пространство единичных окружностей в касательных
- 20. Однородные трехмерные геометрии которые образуют группу относительно операции умножения и на ней задана метрика Sol .
- 21. Геометрическая гипотеза Терстона Неприводимое трехмерное замкнутое многообразие разрезается несжимающимися торами на куски, на которых можно задать
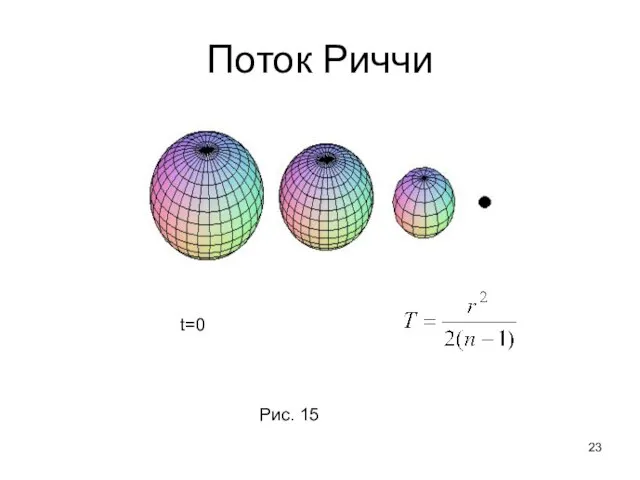
- 22. Поток Риччи Пусть есть риманово неприводимо компактное многообразие, на котором в локальных координатах метрика задается в
- 23. Поток Риччи t=0 Рис. 15
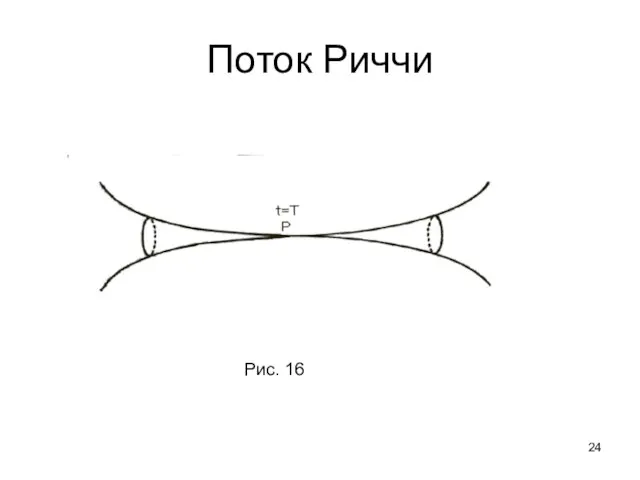
- 24. Поток Риччи Рис. 16
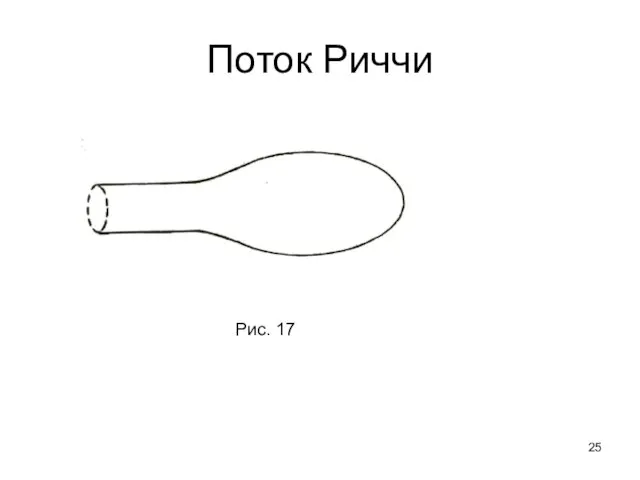
- 25. Поток Риччи Рис. 17
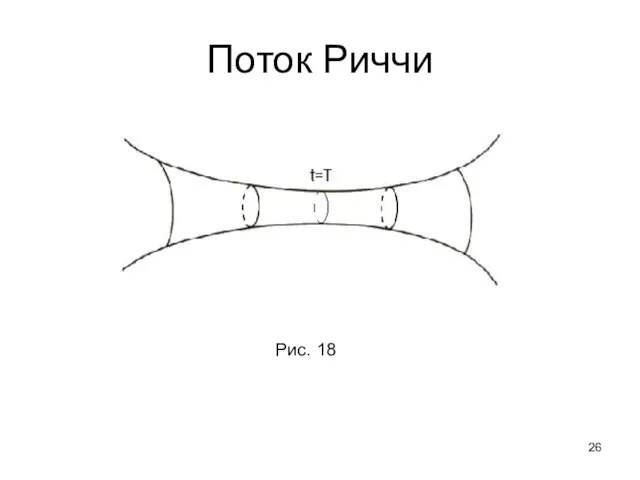
- 26. Поток Риччи Рис. 18
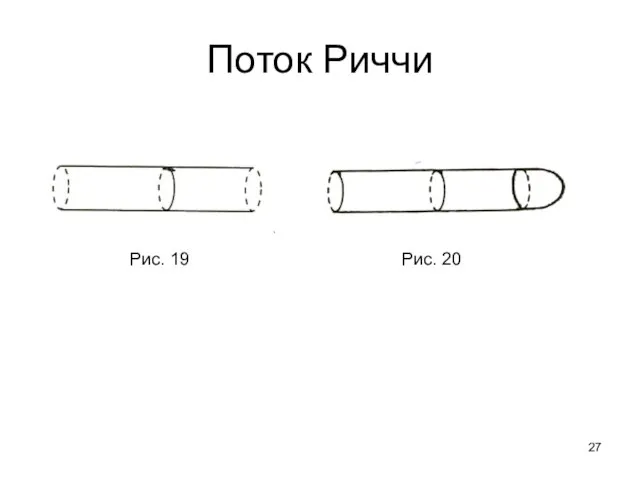
- 27. Поток Риччи Рис. 19 Рис. 20
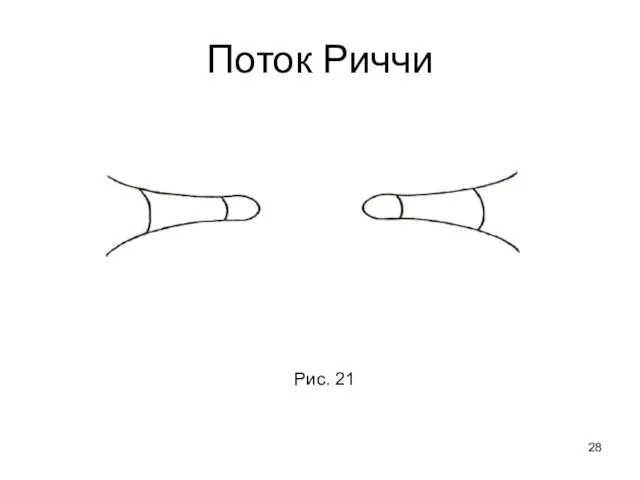
- 28. Поток Риччи Рис. 21
- 30. Скачать презентацию
















 Ромб
Ромб Площади фигур. Зачёт
Площади фигур. Зачёт Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Плоскость представляет с собой -геометрическую фигуру, простирающуюся неограниченно во все стороны.
Плоскость представляет с собой -геометрическую фигуру, простирающуюся неограниченно во все стороны. Площадь прямоугольника
Площадь прямоугольника Объем конуса
Объем конуса Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Параллельные прямые
Параллельные прямые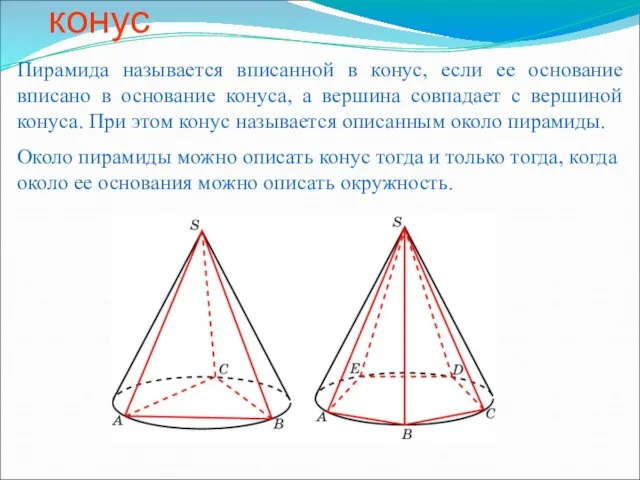 Пирамида, вписанная в конус
Пирамида, вписанная в конус Площадь параллелограмма 9 класс
Площадь параллелограмма 9 класс Цилиндр и конус
Цилиндр и конус Описанная и вписанная окружность
Описанная и вписанная окружность Треугольники 3 класс
Треугольники 3 класс Преобразование плоскости
Преобразование плоскости Смотр общественных знаний
Смотр общественных знаний Правильная пирамида
Правильная пирамида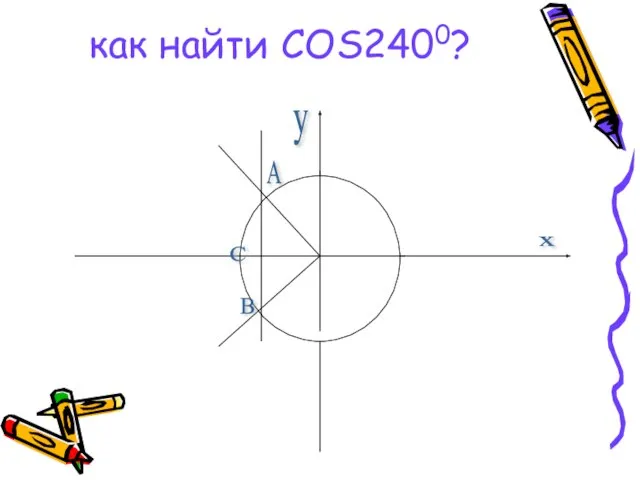 Косинус
Косинус Графический способ решения систем укравнений
Графический способ решения систем укравнений Параллелограмм
Параллелограмм Угол между плоскостями
Угол между плоскостями Выделение элементов и свойств геометрических фигур - презентация по Геометрии_
Выделение элементов и свойств геометрических фигур - презентация по Геометрии_ Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Геометрия
Геометрия Урок 7 (8) Параллельность прямой и плоскости. Решение задач
Урок 7 (8) Параллельность прямой и плоскости. Решение задач Амидекстр
Амидекстр Применение параллелограмма
Применение параллелограмма Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья
Шар(сфера) Выполнила ученица 11 класса: Черниговская Дарья Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса