Слайд 21. ЗАКОН ДВОЙНОГО ОТРИЦАНИЯ.
А=А
Я пойду гулять = Я не не пойду гулять
Двойное

отрицание исключает отрицание.
Слайд 32.ПЕРЕМЕСТИТЕЛЬНЫЙ (КОММУНИКАТИВНЫЙ) ЗАКОН.
- Для логического сложения:
АvB = BvA
Ты или я = Я

или ты
Для логического умножения:
A&B = B&A
Собака и кошка = Кошка и собака
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
Слайд 43. СОЧЕТАТЕЛЬНЫЙ (АССОЦИАТИВНЫЙ) ЗАКОН.
- Для логического сложения:
(AvB)vC = Av(BvC)
Для логического умножения:
(A&B)&C =

A&(B&C)
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
Слайд 54. РАСПРЕДЕЛИТЕЛЬНЫЙ (ДИСТРИБУТИВНЫЙ) ЗАКОН.
Для логического сложения:
(AvB)vC= (A&C)v(B&C)
Для логического умножения:
(A&B)vC = (AvC)&(BvC)
Определяет правила

выноса общего высказывания за скобку.
Слайд 65. ЗАКОН ОБЩЕЙ ИНВЕРСИИ (ЗАКОНЫ ДЕ МОРГАНА).
Для логического сложения:
AvB = A&B
Для логического

умножения:
A&B = AvB
Слайд 76. ЗАКОНЫ ИДЕМПОТЕНТНОСТИ.
Для логического сложения:
AvA = A
Для логического умножения:
A&A = A
Закон означает

отсутствие показателей степени.
Слайд 87. ЗАКОНЫ ИСКЛЮЧЕНИЯ КОНСТАНТ.
Для логического сложения:
Av1 = 1, Av0 = A
Для логического

умножения:
A&1 = A, A&0 = 0
Слайд 98. ЗАКОН ПРОТИВОРЕЧИЯ.
A&A = 0
Невозможно, чтобы противоречащие высказывания были одновременно истинными.

Слайд 109. ЗАКОН ИСКЛЮЧЕНИЯ ТРЕТЬЕГО.
AvA = 1
Из двух противоречащих высказываний об одном и

том же предмете одно всегда истинно, а второе – ложное, третьего не надо.
Слайд 1110. ЗАКОН ПОГЛОЩЕНИЯ.
Для логического сложения:
Av(A&B) = A
Для логического умножения:
A&(AvB) = A

Слайд 1211. ЗАКОН ИСКЛЮЧЕНИЯ (СКЛЕИВАНИЯ).
- Для логического сложения:
(A&B)v(A&B) = B
- Для логического

умножения:
(AvB)&(AvB) = B
Слайд 1312. ЗАКОН КОНТРАПОЗИЦИИ (ПРАВИЛО ПЕРЕВЁРТЫВАНИЯ).
(A⟺B) = (B⟺A)













 Почему квадрат?
Почему квадрат? Координаты вектора
Координаты вектора Четырехугольники
Четырехугольники Измерение углов
Измерение углов Площадь параллелограмма и треугольника
Площадь параллелограмма и треугольника Основные труды и биография Декарта
Основные труды и биография Декарта Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Египетский треугольник
Египетский треугольник Понятие объема. Объем призмы
Понятие объема. Объем призмы Вводное повторение курса геометрии
Вводное повторение курса геометрии Уравнение прямой в пространстве
Уравнение прямой в пространстве Знакомство с миром геометрии
Знакомство с миром геометрии Задания на клетчатой бумаге
Задания на клетчатой бумаге Прямоугольный параллелепипед
Прямоугольный параллелепипед Симметрия правит миром
Симметрия правит миром Установление соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_
Установление соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_ Равнобедренная трапеция
Равнобедренная трапеция Перпендикуляр и наклонная
Перпендикуляр и наклонная Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн
Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн Многогранники вокруг нас
Многогранники вокруг нас Решение задач на тему «Прямоугольник. Ромб. Квадрат»
Решение задач на тему «Прямоугольник. Ромб. Квадрат» Прямоугольные треугольники
Прямоугольные треугольники Свойства трапеции. Фабер Г.Н.-учитель математики
Свойства трапеции. Фабер Г.Н.-учитель математики Векторы
Векторы Теорема Пифагора задачи
Теорема Пифагора задачи Трисекция угла
Трисекция угла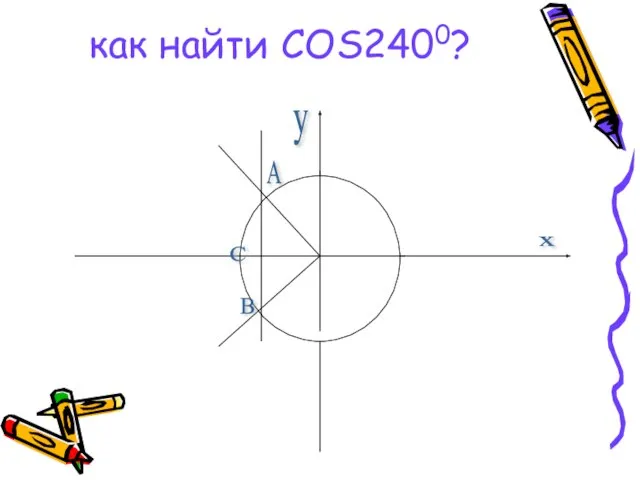 Косинус
Косинус