Содержание
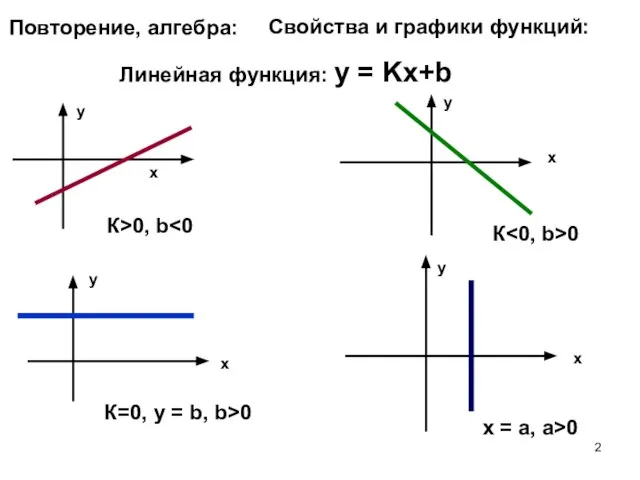
- 2. Повторение, алгебра: Свойства и графики функций: Линейная функция: у = Kх+b х х у у К>0,
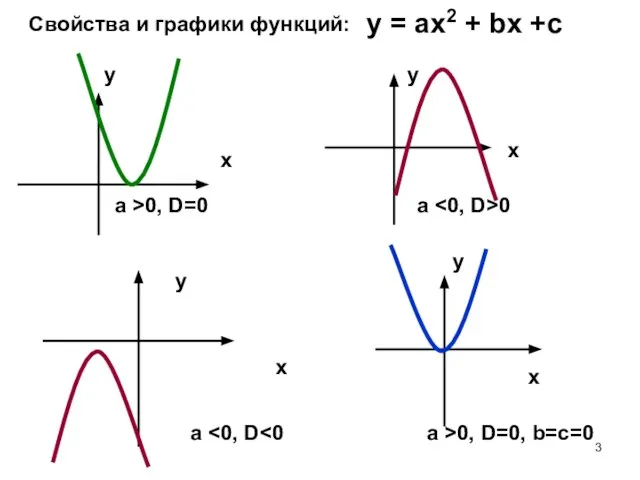
- 3. Свойства и графики функций: у = ах2 + bх +с a >0, D=0 a 0 x
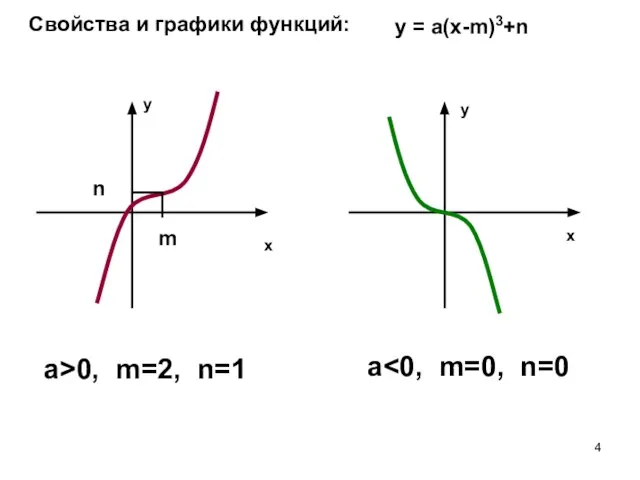
- 4. Свойства и графики функций: y = а(х-m)3+n a>0, m=2, n=1 a m n x x y
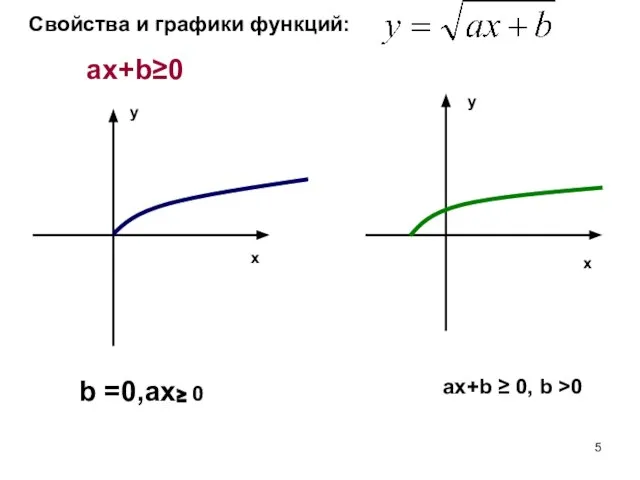
- 5. Свойства и графики функций: ax+b≥0 x x y y b =0,ax≥ 0 ax+b ≥ 0, b
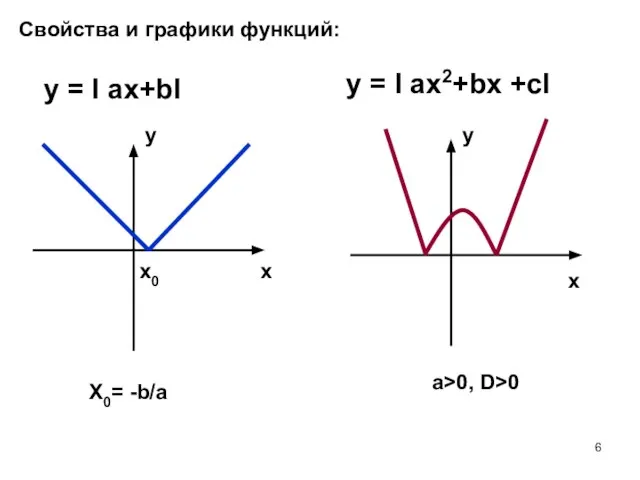
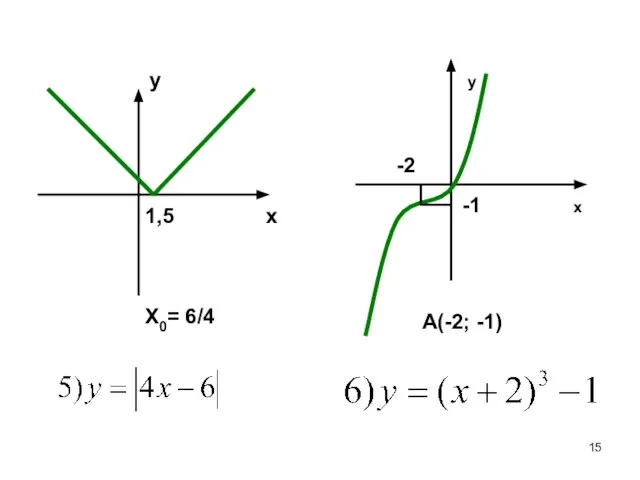
- 6. Свойства и графики функций: y = I ax+bI y = I ax2+bx +cI x0 a>0, D>0
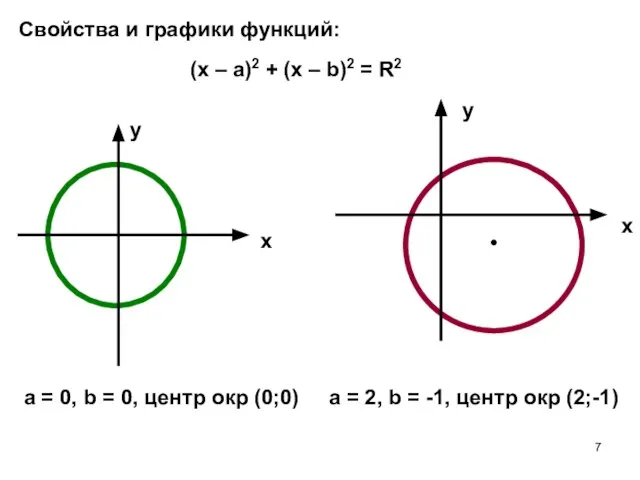
- 7. х х у у (х – а)2 + (х – b)2 = R2 a = 0,
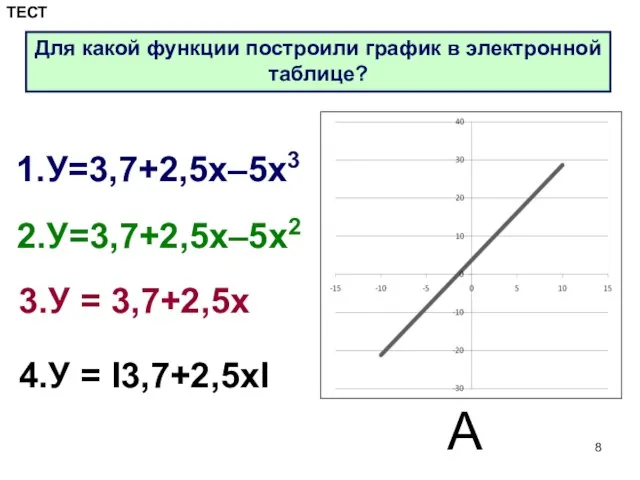
- 8. 1.У=3,7+2,5х–5х3 2.У=3,7+2,5х–5х2 3.У = 3,7+2,5х 4.У = I3,7+2,5хI А Для какой функции построили график в электронной
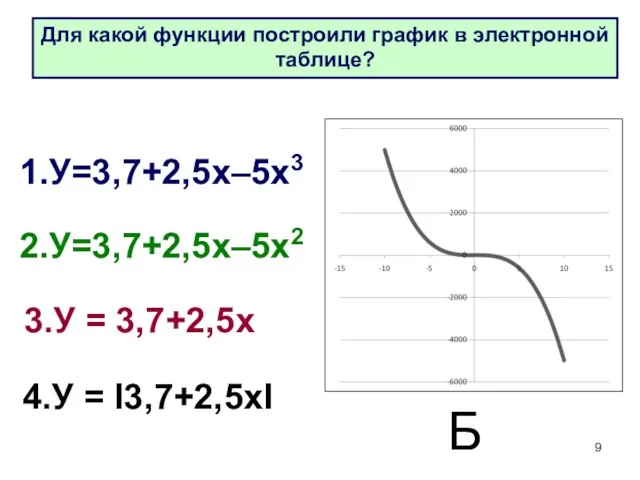
- 9. 1.У=3,7+2,5х–5х3 2.У=3,7+2,5х–5х2 3.У = 3,7+2,5х 4.У = I3,7+2,5хI Б Для какой функции построили график в электронной
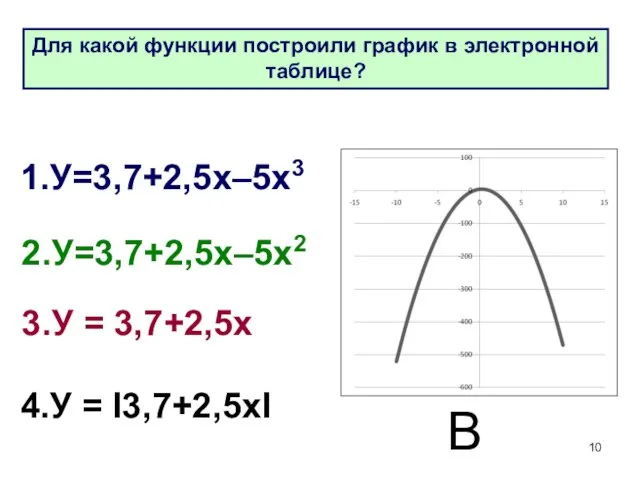
- 10. 1.У=3,7+2,5х–5х3 2.У=3,7+2,5х–5х2 3.У = 3,7+2,5х 4.У = I3,7+2,5хI В Для какой функции построили график в электронной
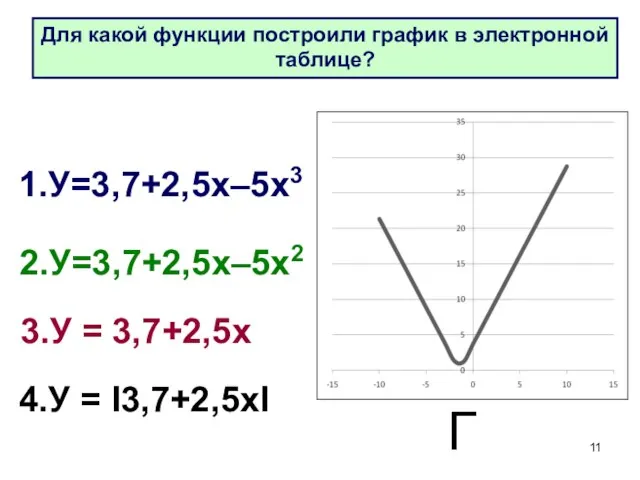
- 11. 4.У = I3,7+2,5хI 1.У=3,7+2,5х–5х3 2.У=3,7+2,5х–5х2 3.У = 3,7+2,5х Г Для какой функции построили график в электронной
- 12. 2) у = х2 - 4х - 5 1) у = 3х - 6 В тетрадях
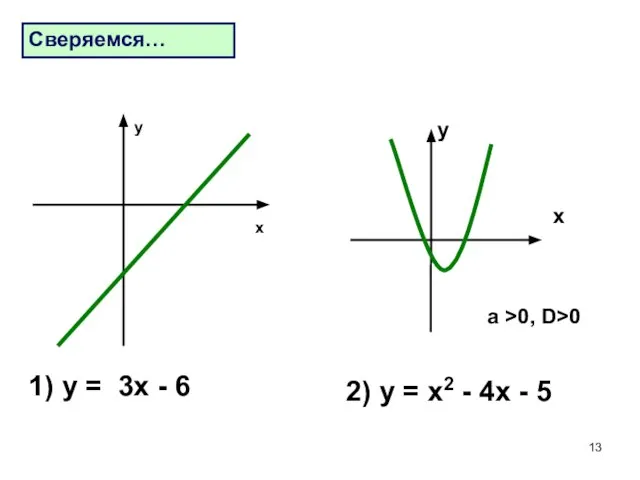
- 13. 1) у = 3х - 6 Сверяемся… х у 2) у = х2 - 4х -
- 14. a x y y a>0, b x 3
- 15. 1,5 X0= 6/4 x y x y A(-2; -1) -2 -1
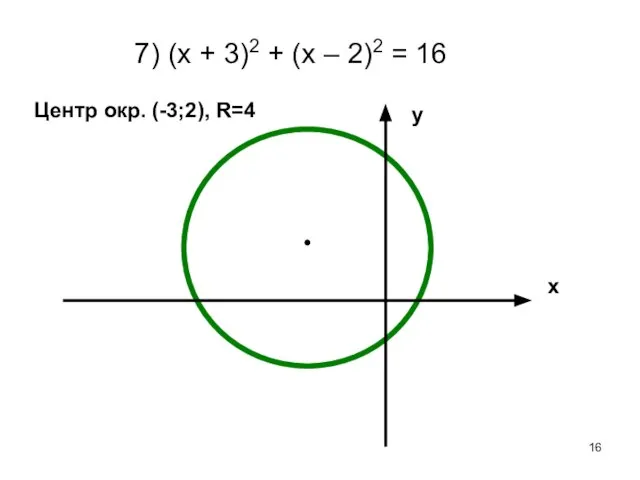
- 16. 7) (х + 3)2 + (х – 2)2 = 16 х у Центр окр. (-3;2), R=4
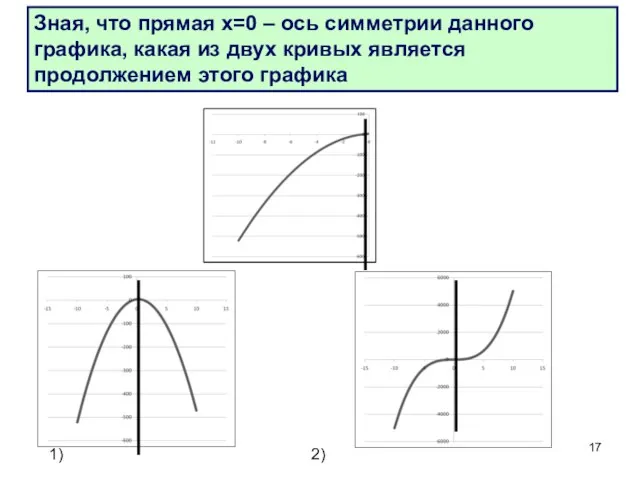
- 17. Зная, что прямая х=0 – ось симметрии данного графика, какая из двух кривых является продолжением этого
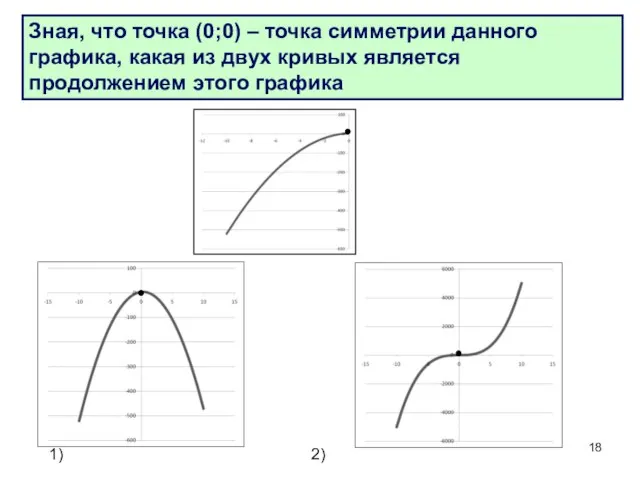
- 18. Зная, что точка (0;0) – точка симметрии данного графика, какая из двух кривых является продолжением этого
- 19. ТЕСТ Какие формулы, написанные при построении графиков в электронной таблице, соответствуют функциям: 1) У=5+ 2х–7х3 2)
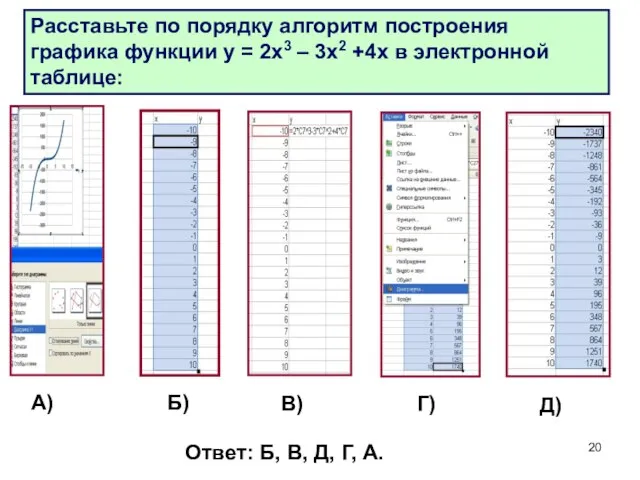
- 20. Расставьте по порядку алгоритм построения графика функции у = 2х3 – 3х2 +4х в электронной таблице:
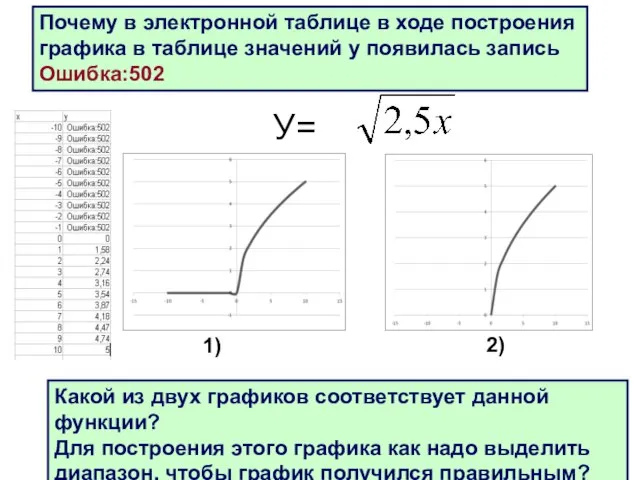
- 21. У= Почему в электронной таблице в ходе построения графика в таблице значений у появилась запись Ошибка:502
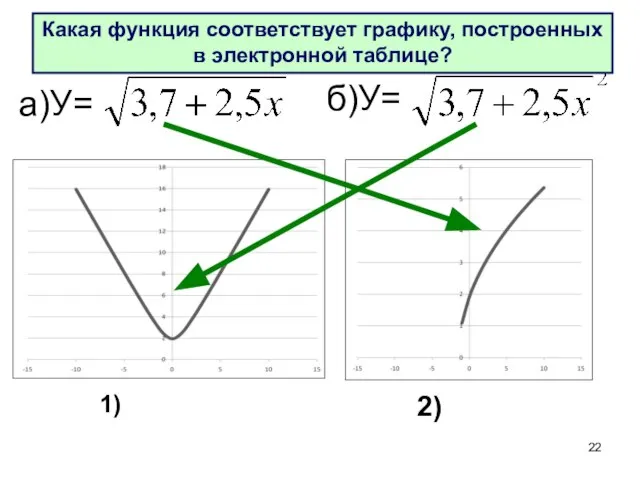
- 22. а)У= б)У= Какая функция соответствует графику, построенных в электронной таблице? 2) 1)
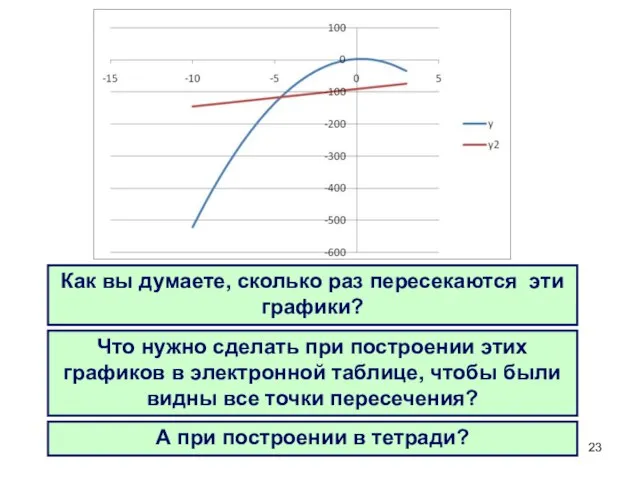
- 23. Как вы думаете, сколько раз пересекаются эти графики? Что нужно сделать при построении этих графиков в
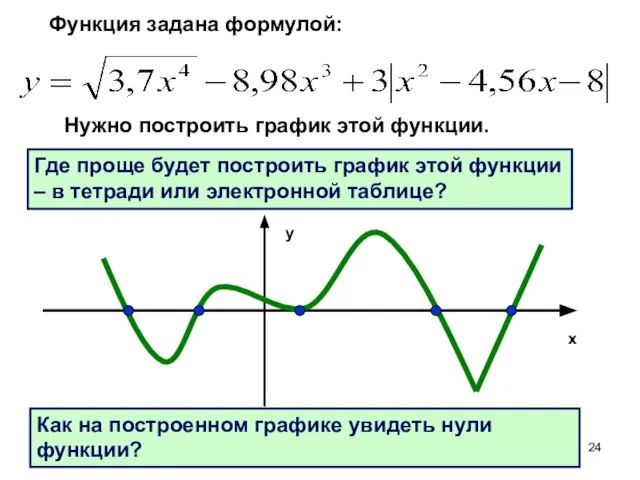
- 24. Функция задана формулой: Нужно построить график этой функции. Где проще будет построить график этой функции –
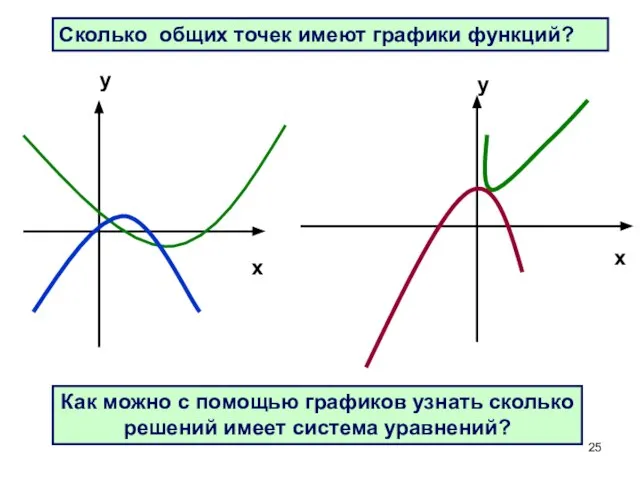
- 25. Сколько общих точек имеют графики функций? Как можно с помощью графиков узнать сколько решений имеет система
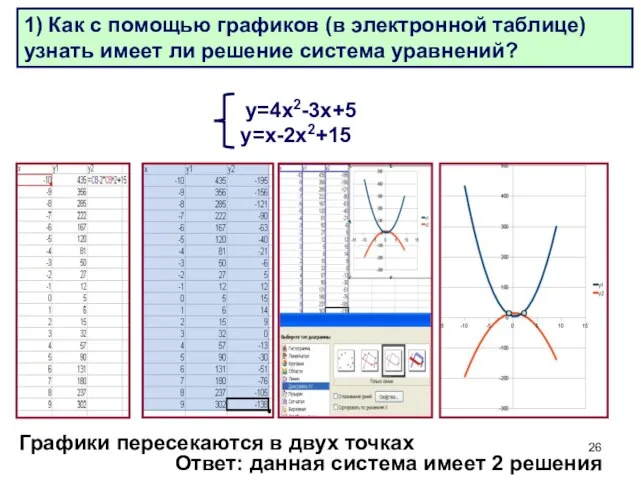
- 26. Объяснение материала: Решаются задачи в электронной таблице: у=4х2-3х+5 у=х-2х2+15 Ответ: данная система имеет 2 решения Графики
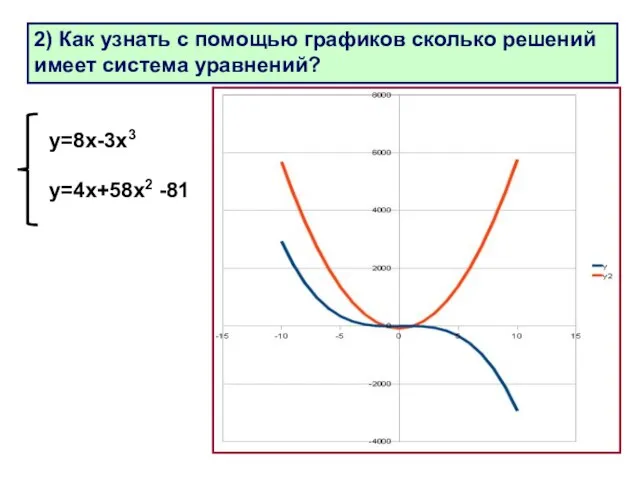
- 27. 2) Как узнать с помощью графиков сколько решений имеет система уравнений? у=8х-3х3 у=4х+58х2 -81
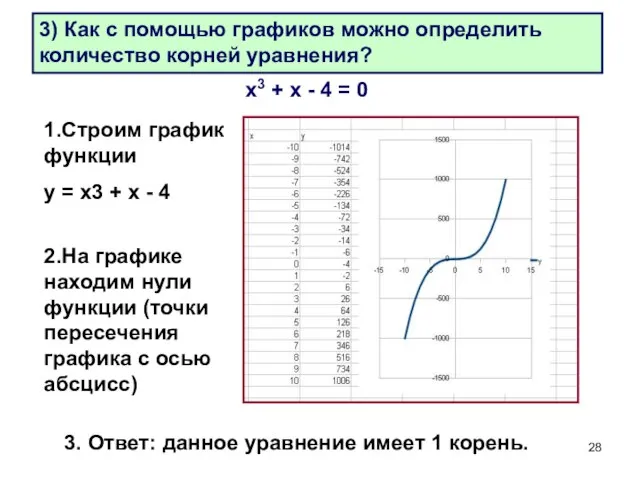
- 28. 3) Как с помощью графиков можно определить количество корней уравнения? х3 + х - 4 =
- 29. 4) Можно ли найти решения данного уравнения? Как это можно сделать? 1способ: Построить график функции и
- 30. Закрепление материала: 1. В электронной таблице найти количество корней системы уравнений: 2. Сколько корней имеет уравнение:
- 31. 3. Найти количество корней системы уравнений, не используя электронную таблицу ( т.е. схематически изобразив графики функций)
- 32. 5) Где быстрее строятся графики: в тетради или электронной таблице? 6) Что нужно соблюдать при построении
- 34. Скачать презентацию

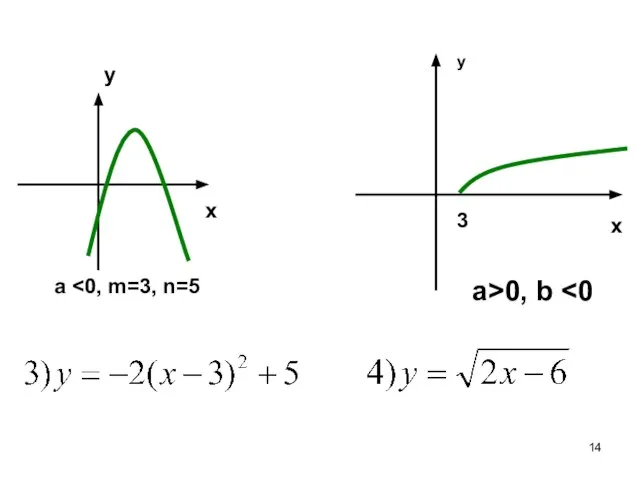





 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием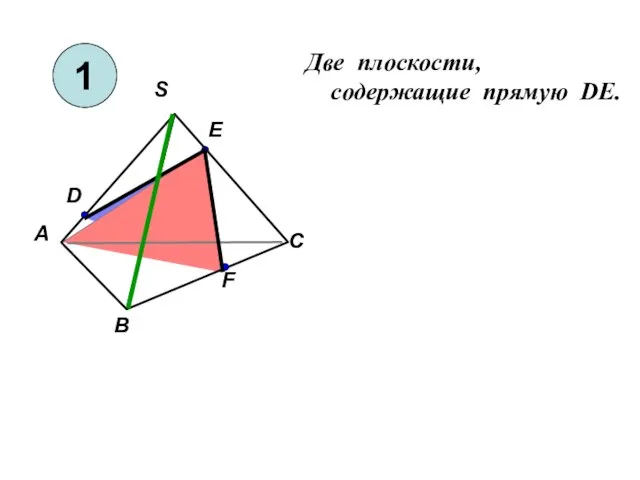 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия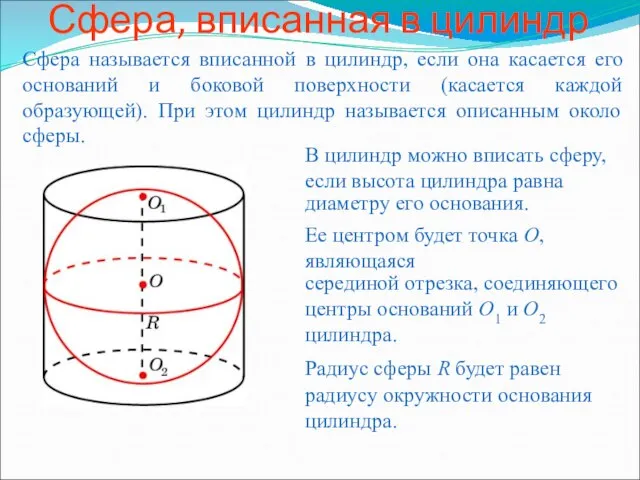 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты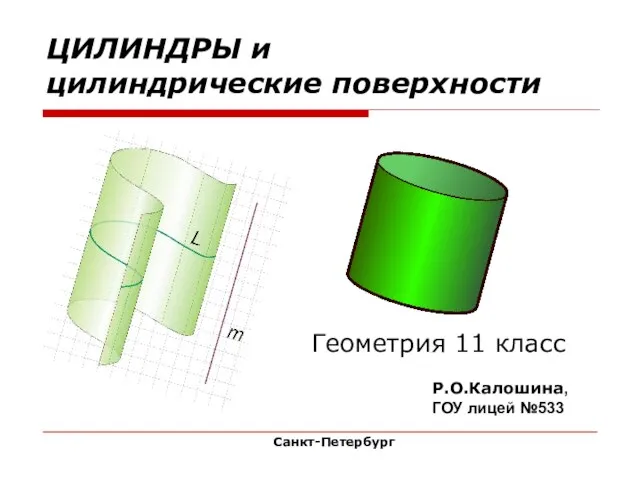 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика