Содержание
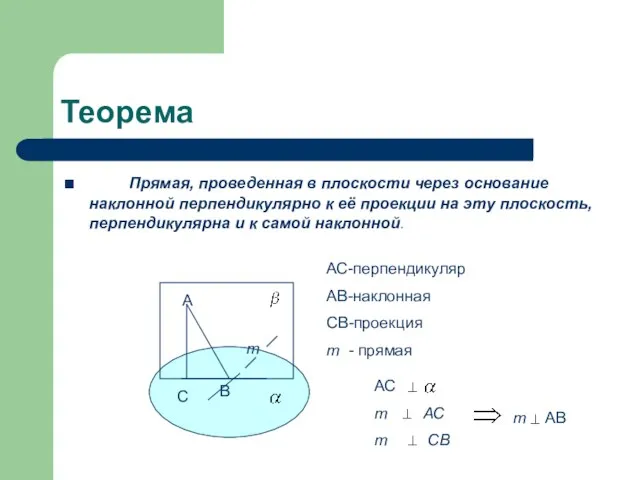
- 2. Теорема Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна
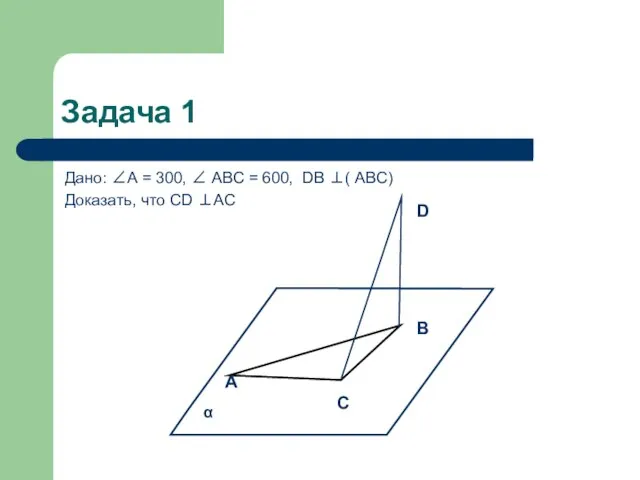
- 3. Задача 1 Дано: ∠А = 300, ∠ АВС = 600, DВ ⊥( АВС) Доказать, что СD
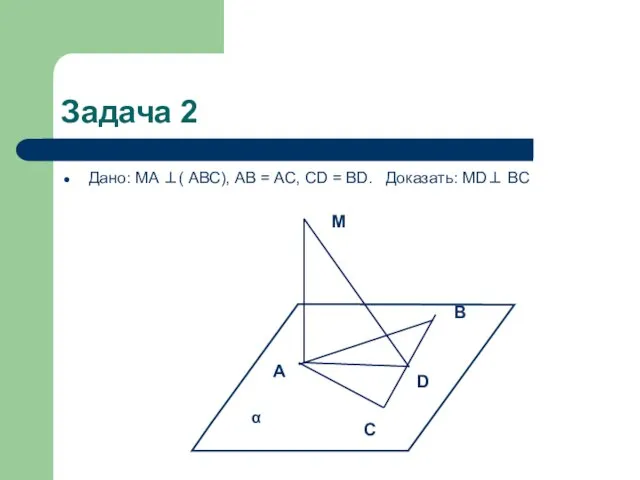
- 4. Задача 2 Дано: MA ⊥( АВС), AB = AC, CD = BD. Доказать: MD⊥ ВС M
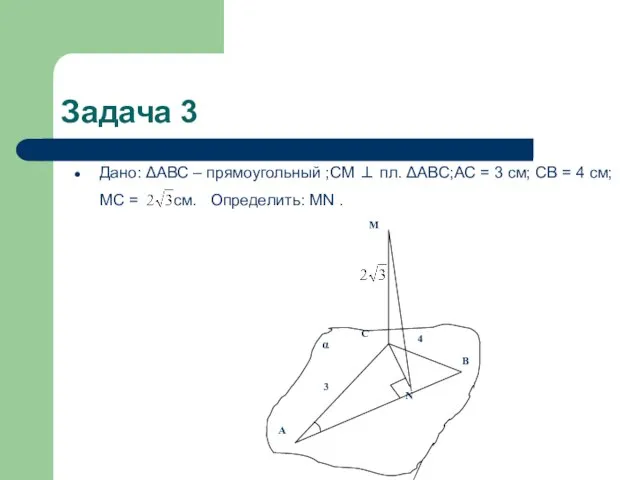
- 5. Задача 3 Дано: ΔАВС – прямоугольный ;СМ ⊥ пл. ΔАВС;АС = 3 см; СВ = 4
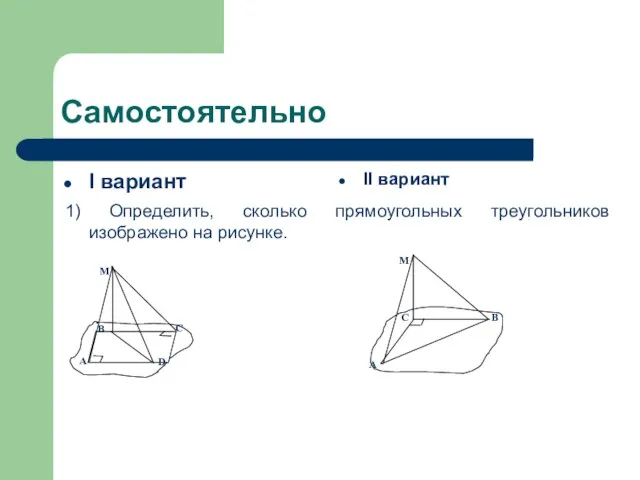
- 6. Самостоятельно I вариант II вариант
- 8. Скачать презентацию
 Координатный метод
Координатный метод Пирамиды
Пирамиды Упражнения со спичками (занятие 9)
Упражнения со спичками (занятие 9) Треугольник Устные задачи
Треугольник Устные задачи Амидекстр
Амидекстр Правила нанесения размеров на чертежах
Правила нанесения размеров на чертежах ЭЛЛИПС
ЭЛЛИПС Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс Равнобедренный треугольник
Равнобедренный треугольник Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Шар, вписанный в пирамиду, призму, конус
Шар, вписанный в пирамиду, призму, конус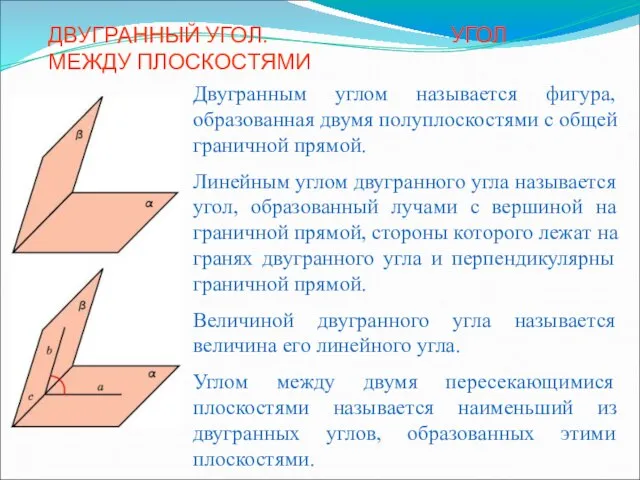 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями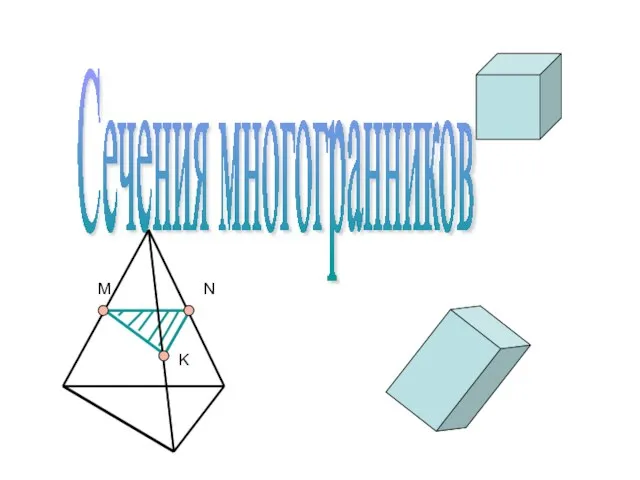 Сечения многогранников
Сечения многогранников Правильные многогранники
Правильные многогранники Геометрия
Геометрия Тетраэдр
Тетраэдр Показательная функция и её применение
Показательная функция и её применение Чудеса симметрии
Чудеса симметрии Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ вид разреза сечения
вид разреза сечения Основные труды и биография Декарта
Основные труды и биография Декарта Осевая симметрия (6 класс)
Осевая симметрия (6 класс) Геометрия 7 класс Геометрия 7 класс
Геометрия 7 класс Геометрия 7 класс Египетский треугольник
Египетский треугольник Цилиндр и конус - презентация по Геометрии
Цилиндр и конус - презентация по Геометрии Прямоугольник и его свойства
Прямоугольник и его свойства Сфера, вписанная в многогранник
Сфера, вписанная в многогранник Биссектриса угла
Биссектриса угла