Содержание
- 2. Цели: Цели урока: ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника; доказать теорему о
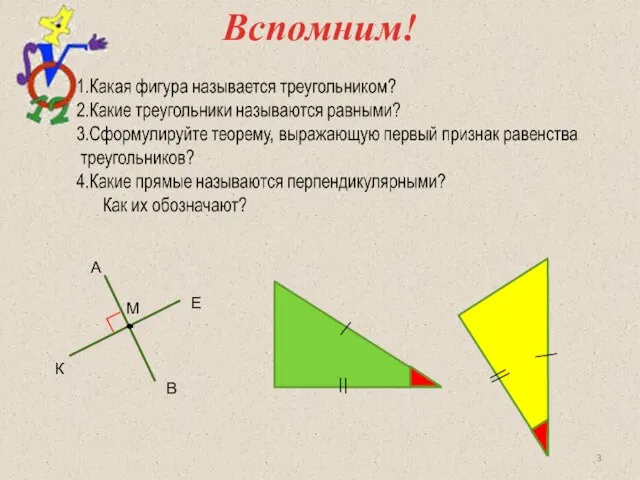
- 3. Вспомним! ∟
- 4. Проверка домашнего задания № 97, № 98, № 99
- 5. а Н А Изучение нового материала. Построение перпендикуляра к прямой
- 6. Практическое задание - Начертите прямую а и отметьте точку А, - Через точку проведите прямую перпендикулярную
- 7. Теорема о перпендикуляре Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и
- 8. Докажем теорему о существовании перпендикуляра к прямой. Теорема: Из точки, не лежащей на прямой, можно провести
- 9. Докажем, что из точки A можно провести только один перпендикуляр к прямой . Если предположить, что
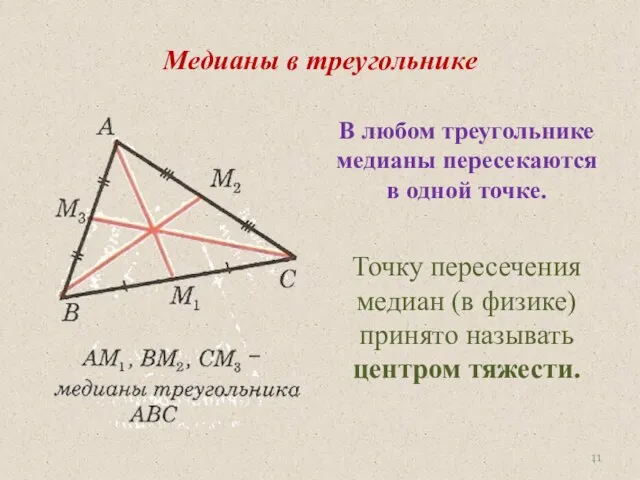
- 10. Медиана. Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника . A C B
- 11. Медианы в треугольнике В любом треугольнике медианы пересекаются в одной точке. Точку пересечения медиан (в физике)
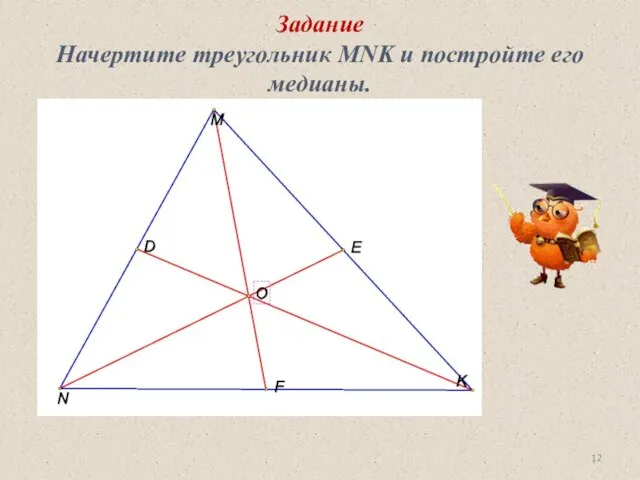
- 12. Задание Начертите треугольник MNK и постройте его медианы.
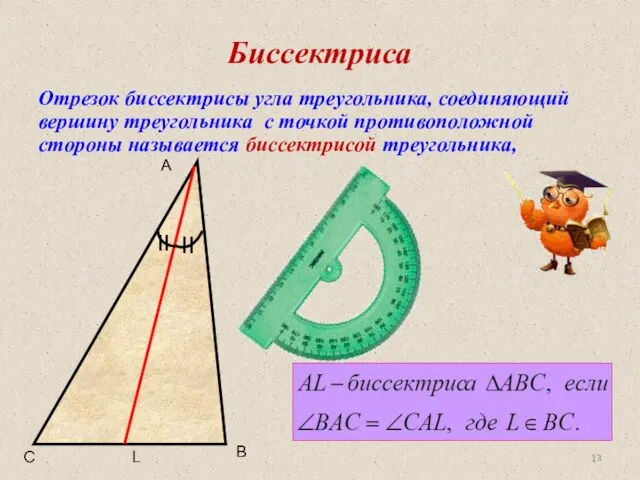
- 13. Биссектриса Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника, A
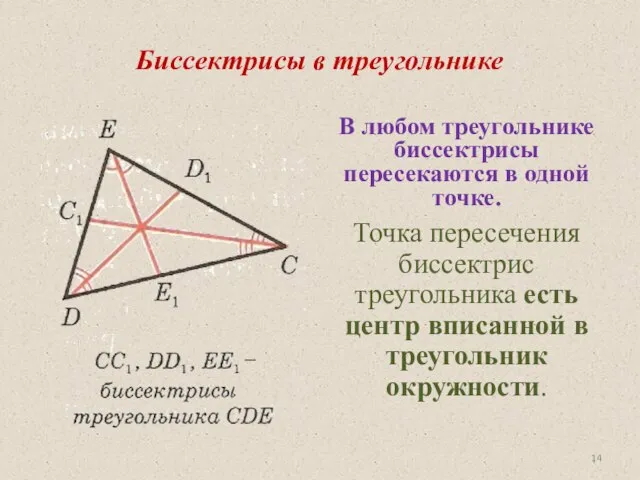
- 14. Биссектрисы в треугольнике В любом треугольнике биссектрисы пересекаются в одной точке. Точка пересечения биссектрис треугольника есть
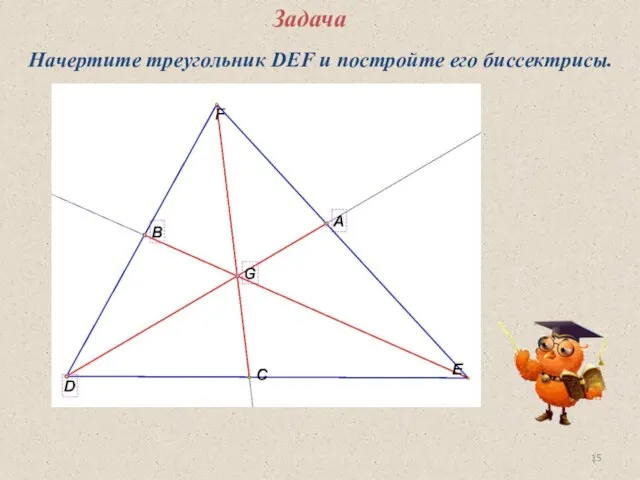
- 15. Задача Начертите треугольник DEF и постройте его биссектрисы.
- 16. Высота Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону называется высотой треугольника
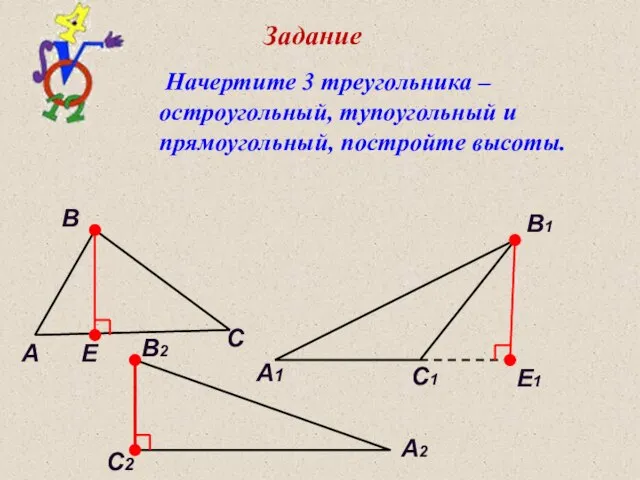
- 17. Задание C C1 C2 A A1 A2 B B1 B2 E E1 Начертите 3 треугольника –
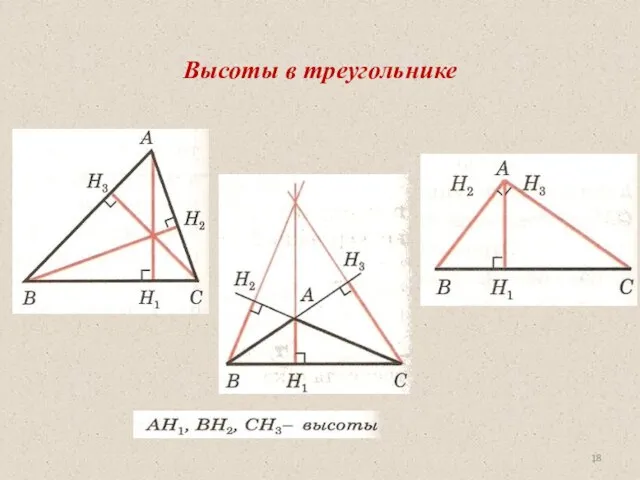
- 18. Высоты в треугольнике
- 19. Закрепление изученного материала 1.Решить задачи №105 (б), 106 (б) письменно. 2.Решите задания с самопроверкой Дано: АО-медиана
- 20. Ответить на вопросы: Какой отрезок называется перпендикуляром к прямой? Какой отрезок называется медианой треугольника? Сколько медиан
- 22. Скачать презентацию











 Геометрия в жизни
Геометрия в жизни Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах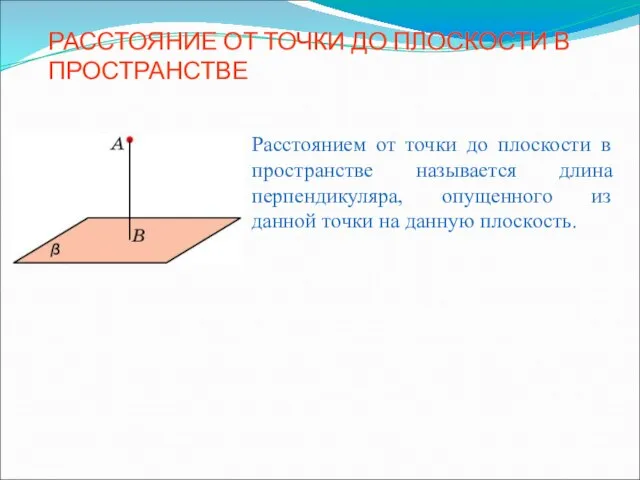 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Прямоугольник
Прямоугольник Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс Задачи на готовых чертежах
Задачи на готовых чертежах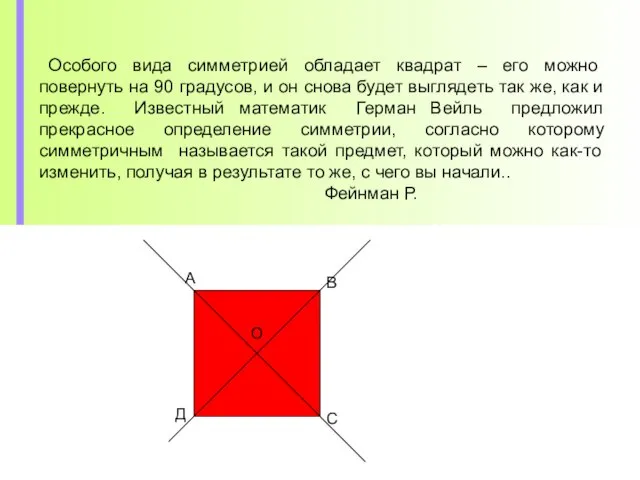 Презентация на тему: Параллельный перенос
Презентация на тему: Параллельный перенос Флексагоны
Флексагоны От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Высоты треугольника
Высоты треугольника Преобразования на плоскости
Преобразования на плоскости Треугольник Устные задачи
Треугольник Устные задачи Знакомство с миром геометрии
Знакомство с миром геометрии Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн
Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн Музей истории четырёхугольников
Музей истории четырёхугольников Четырехугольники
Четырехугольники Многогранники и кристаллы
Многогранники и кристаллы Построение теней
Построение теней Параллельность в пространстве
Параллельность в пространстве ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга
ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга Двугранный угол (10-11 класс) - презентация по Геометрии_
Двугранный угол (10-11 класс) - презентация по Геометрии_ Симметрия
Симметрия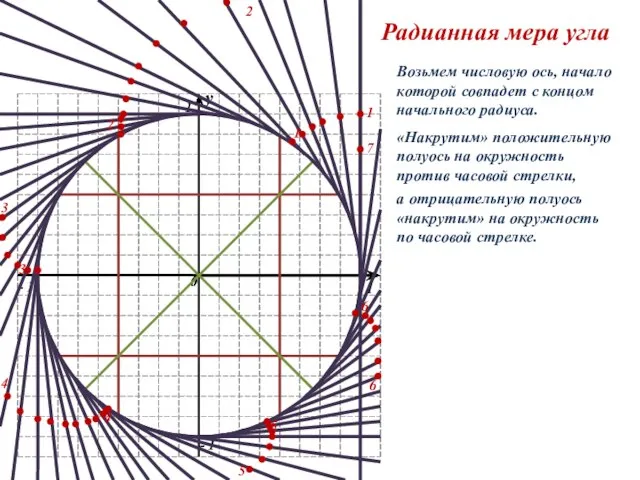 Радианная мера угла
Радианная мера угла Геометрия.Введение. Аксиоматика.
Геометрия.Введение. Аксиоматика. Сумма двух векторов Геометрия -9 Урок 4
Сумма двух векторов Геометрия -9 Урок 4 Разрезание и складывание плоских фигур
Разрезание и складывание плоских фигур Геометрия 7 класс Геометрия 7 класс
Геометрия 7 класс Геометрия 7 класс Фракталы – геометрия природы
Фракталы – геометрия природы