Содержание
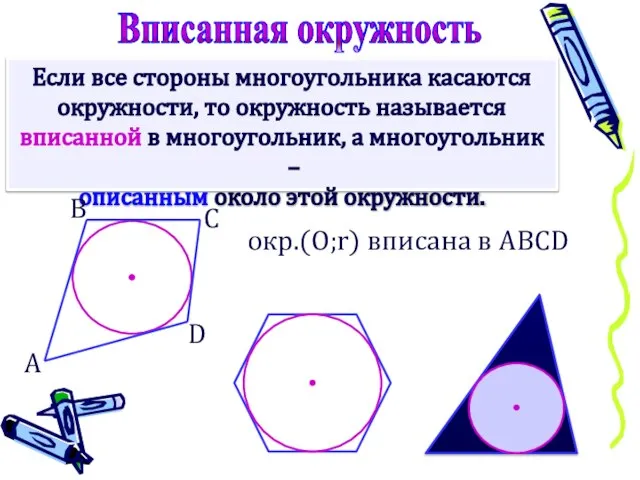
- 2. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным
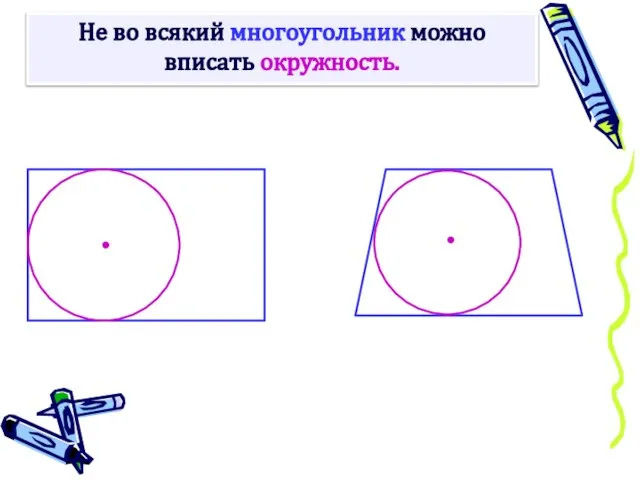
- 3. Не во всякий многоугольник можно вписать окружность.
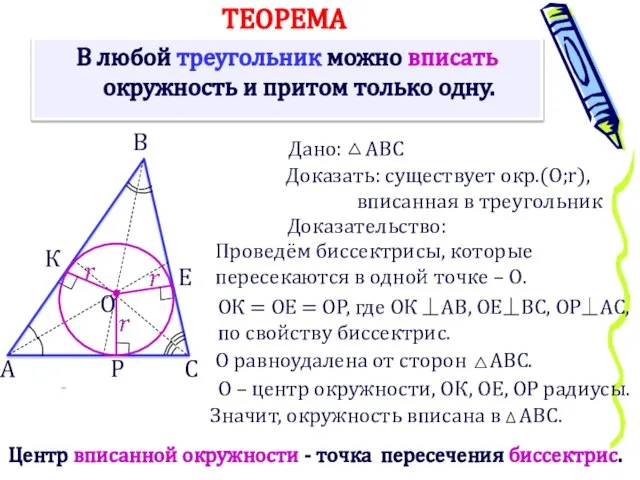
- 4. В любой треугольник можно вписать окружность и притом только одну. А Доказать: существует окр.(О;r), вписанная в
- 5. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. А Площадь треугольника
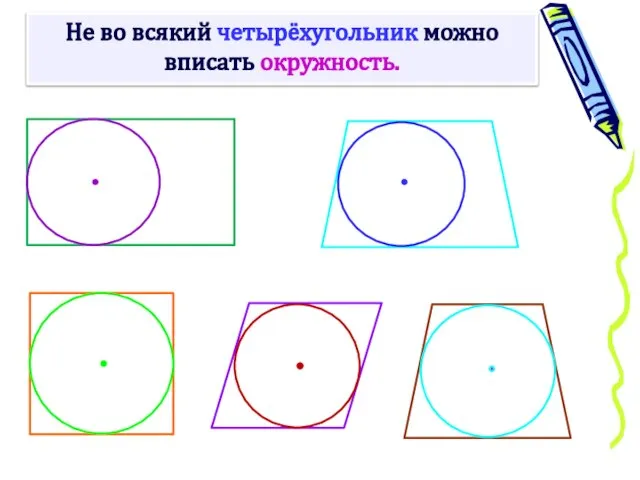
- 6. Не во всякий четырёхугольник можно вписать окружность.
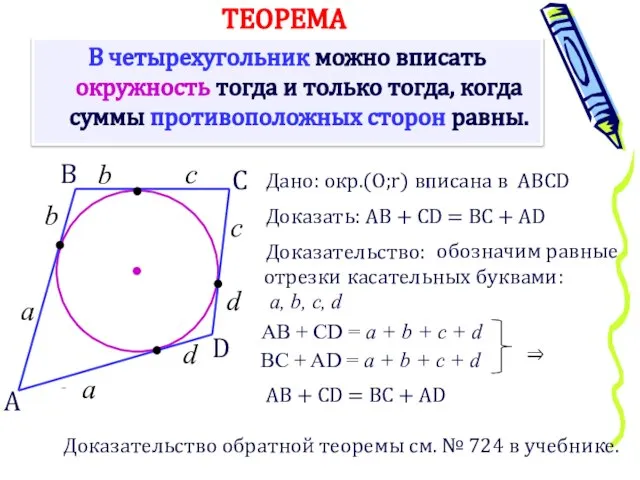
- 7. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны. ТЕОРЕМА А
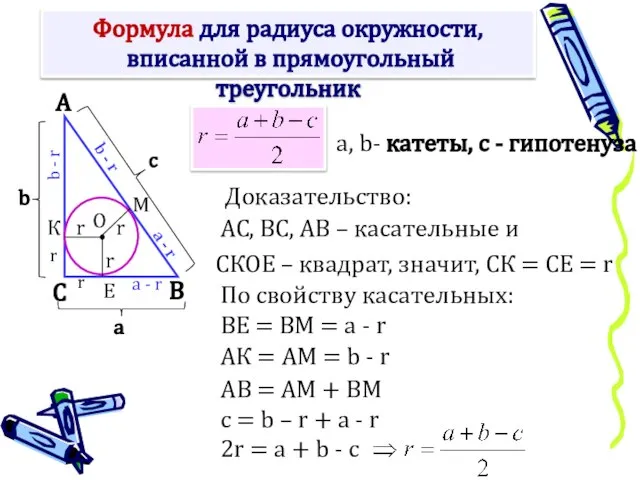
- 8. Формула для радиуса окружности, вписанной в прямоугольный треугольник Доказательство: СКОЕ – квадрат, значит, СК = СЕ
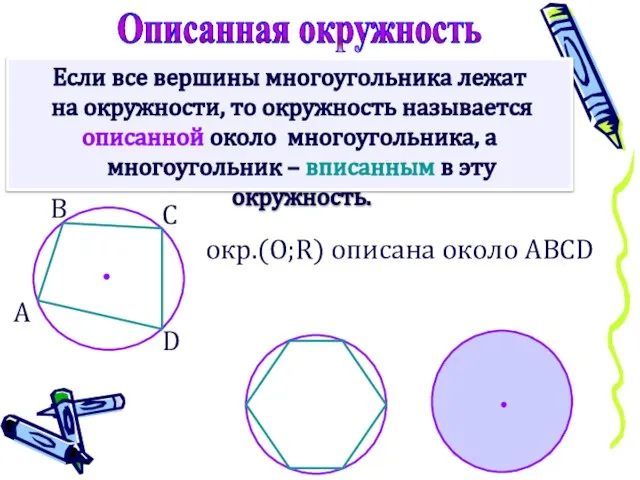
- 9. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник –
- 10. Не около всякого многоугольника можно описать окружность.
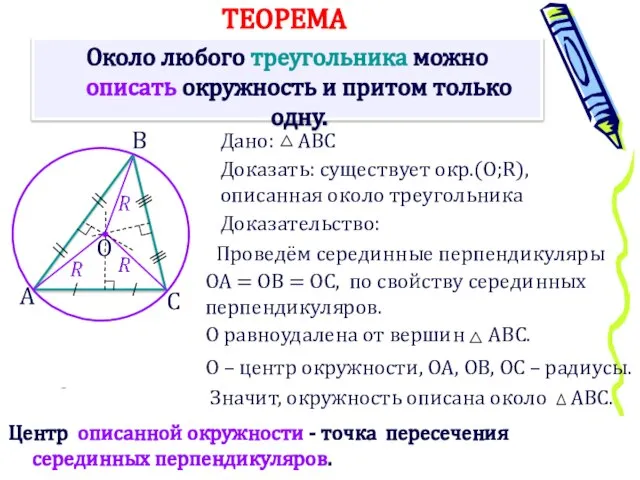
- 11. Около любого треугольника можно описать окружность и притом только одну. Доказать: существует окр.(О;R), описанная около треугольника
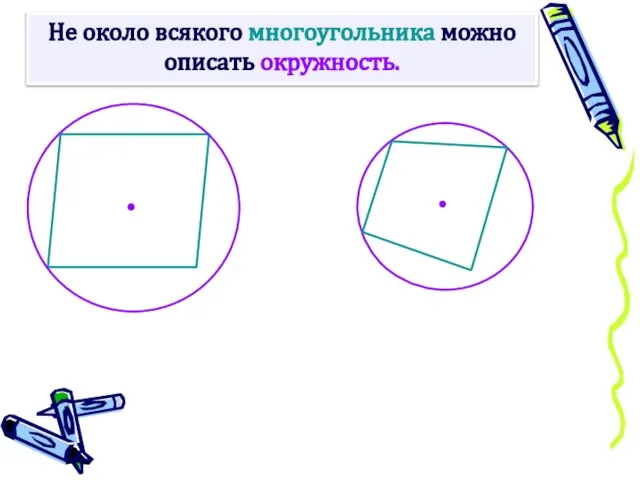
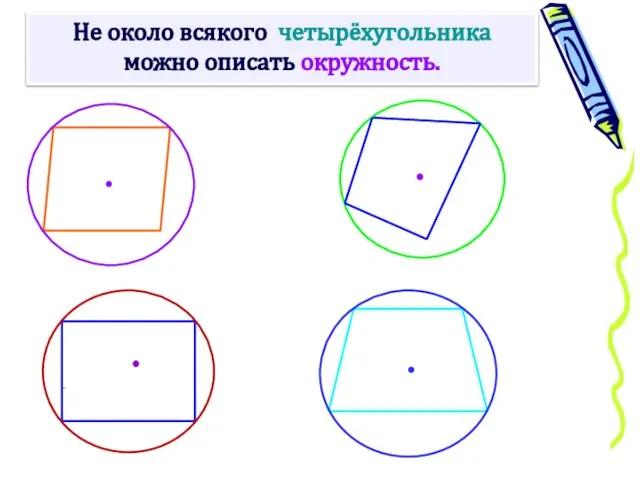
- 12. Не около всякого четырёхугольника можно описать окружность.
- 14. Скачать презентацию

 Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Векторы 9 класс
Векторы 9 класс Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса  Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)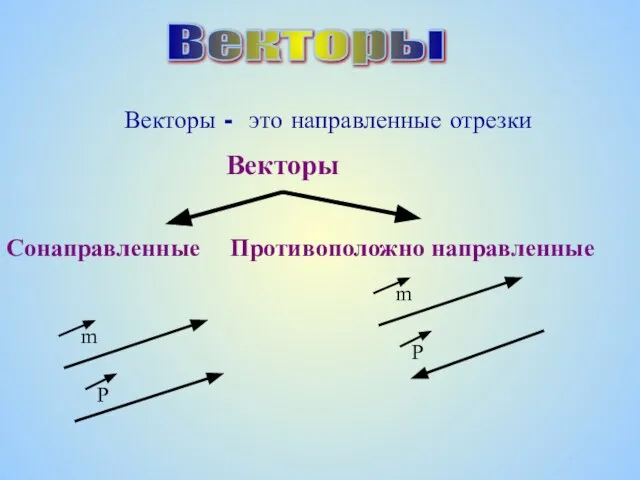 Векторы: Знакомство
Векторы: Знакомство Тела и поверхности вращения
Тела и поверхности вращения Теорема Пифагора задачи
Теорема Пифагора задачи Перпендикулярные прямые 7 класс
Перпендикулярные прямые 7 класс Окружность и круг
Окружность и круг Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса Анализ геометрической формы предмета
Анализ геометрической формы предмета Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Плоскость
Плоскость Путешествие в страну Геометрия
Путешествие в страну Геометрия Решение задач по курсу геометрии
Решение задач по курсу геометрии Окружности
Окружности Теорема синусов 9 класс
Теорема синусов 9 класс Пирамиды
Пирамиды Приготовьтесь к построению
Приготовьтесь к построению Преобразования на плоскости
Преобразования на плоскости Флексагоны флексоры
Флексагоны флексоры Следствия из аксиом стереометрии Упражнения по теме
Следствия из аксиом стереометрии Упражнения по теме Сфера и шар 9 класс
Сфера и шар 9 класс Фракталы и их применение в наши дни.
Фракталы и их применение в наши дни. Правильные многогранники
Правильные многогранники Правильные выпуклые многогранники
Правильные выпуклые многогранники Круг и окружность
Круг и окружность