Решение комбинированных задач с помощью графов
Содержание
- 1. Решение комбинированных задач с помощью графов
- 2. Вопросы к уроку. • Чем занимается комбинаторика?
- 3. 1.Чем занимается комбинаторика? • Комбинаторика-раздел математики ,рассматривающий
- 4. 2.Что такое граф? • Граф-геометрическая фигура,состоящая из точек(вершины графа) и линий,их соединяющих(рёбра графа).
- 5. Примеры графов.
- 6. Примеры графов
- 7. Задача №1 Андрей, Борис, Виктор и Григорий
- 8. Задача №2 Андрей, Борис, Виктор и Григорий
- 9. Задача №3 У Лёвы 2 конверта: обычный
- 10. Задача №4 Ужасные грабители Кнопка и Скрёпка
- 11. Задача №5 Сколько двузначных чисел можно составить
- 12. Задача № Сколько трёхзначных чисел можно составить
- 13. •
- 14. •
- 15. Задача № Сколько трёхзначных чисел можно записать
- 16. Задача №(устно) Сколькими способами Петя и Вова
- 17. «Правило произведения». • Если существует n вариантов
- 18. Задача № • № .Антон, Борис и
- 19. 1 место 2 место 3 место
- 20. Задача № • № .В пятницу у
- 21. А Р Ф И Р Ф Ф ФФ Ф Ф
- 22. Скачать презентацию
- 23. Похожие презентации
Вопросы к уроку. • Чем занимается комбинаторика? • Что такое граф? • Какие задачи относятся к комбинаторным? • Как решаются комбинаторные задачи с помощью графов?
Слайды презентации
Слайд 1
Тема урока:
«Решение комбинаторных
задач с помощью графов»
Слайд 2
Вопросы к уроку.
•
Чем занимается комбинаторика?
•
Что такое граф?
•
Какие задачи относятся к
комбинаторным? • Как решаются комбинаторные задачи с помощью графов?
Слайд 3
1.Чем занимается комбинаторика?
•
Комбинаторика-раздел математики
,рассматривающий вопросы(задачи),
связанные с подсчётом числа
всевозможных комбинаций из элементов данного конечного множества при сделанных
исходных предположениях.
Слайд 4
2.Что такое граф?
•
Граф-геометрическая
фигура,состоящая из точек(вершины
графа) и линий,их соединяющих(рёбра
графа).
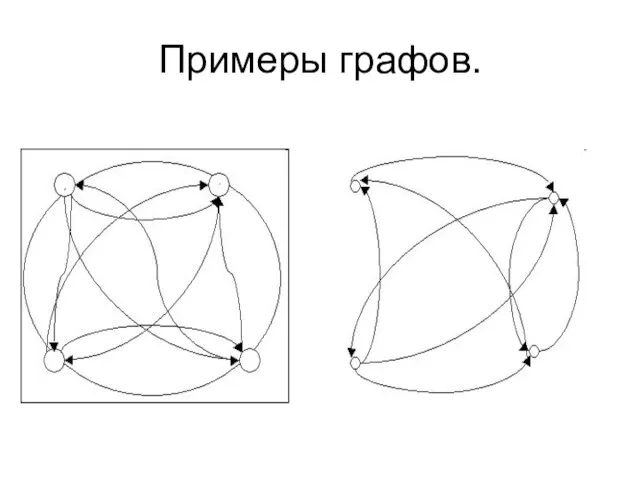
Слайд 5
Примеры графов.
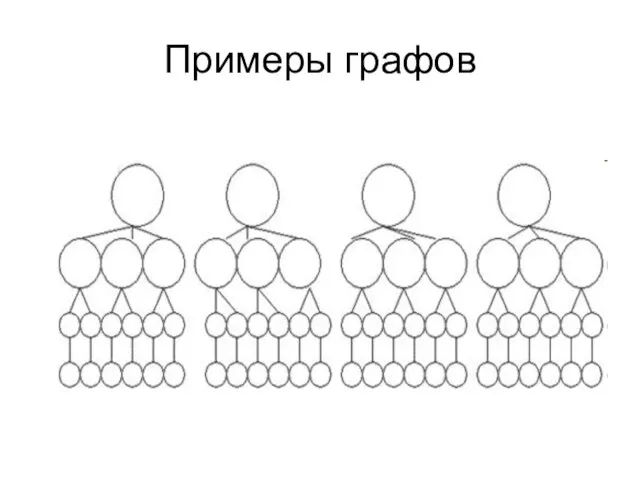
Слайд 6
Примеры графов
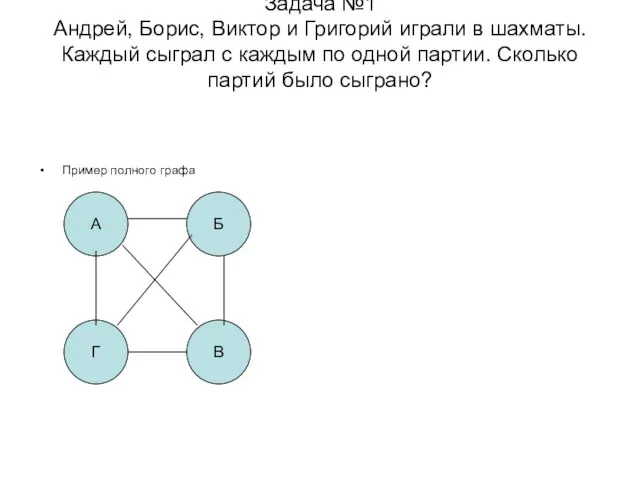
Слайд 7
Задача №1
Андрей, Борис, Виктор и Григорий играли в шахматы.
Каждый
сыграл с каждым по одной партии. Сколько партий было
сыграно? • Пример полного графа А Б Г В
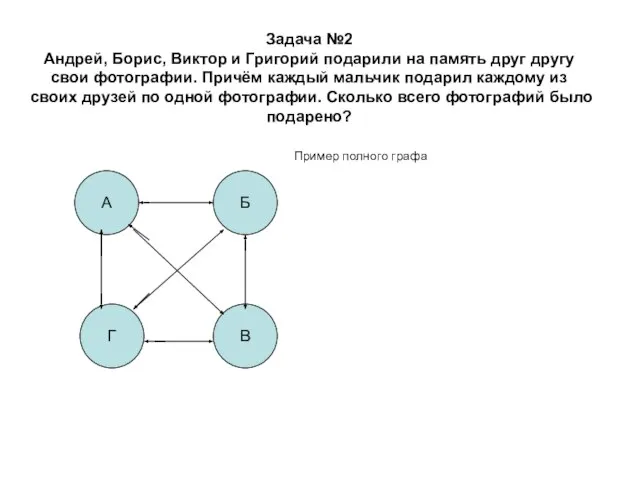
Слайд 8
Задача №2
Андрей, Борис, Виктор и Григорий подарили на память друг
другу свои фотографии. Причём каждый мальчик подарил каждому из
своих друзей по одной фотографии. Сколько всего фотографий было подарено?
Пример полного графа А Г Б В
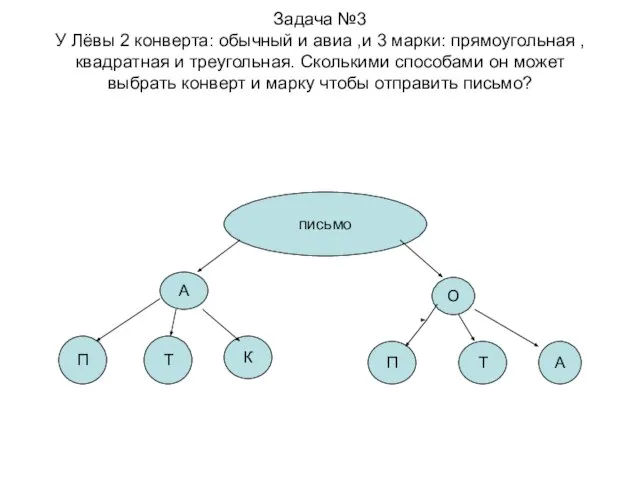
Слайд 9
Задача №3
У Лёвы 2 конверта: обычный и авиа ,и 3
марки: прямоугольная , квадратная и треугольная. Сколькими способами он
может выбрать конверт и марку чтобы отправить письмо? письмо А О П Т К П
Т А
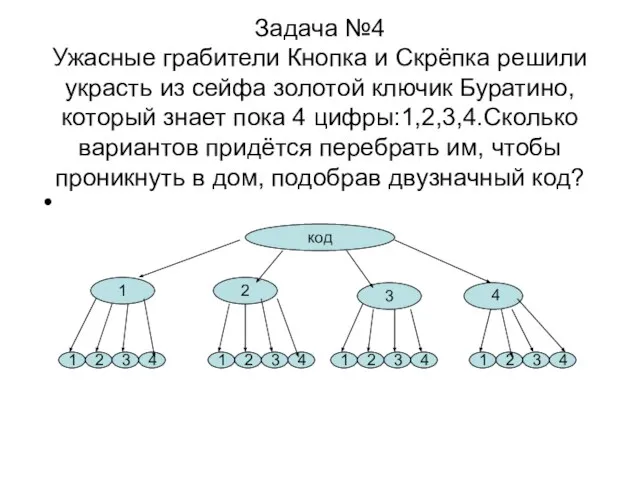
Слайд 10
Задача №4
Ужасные грабители Кнопка и Скрёпка решили
украсть из сейфа
золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько вариантов
придётся перебрать им, чтобы проникнуть в дом, подобрав двузначный код? •
код 1 2 3 1 2 43 1 2 3 4 1 2 3 4 1 2 3 44
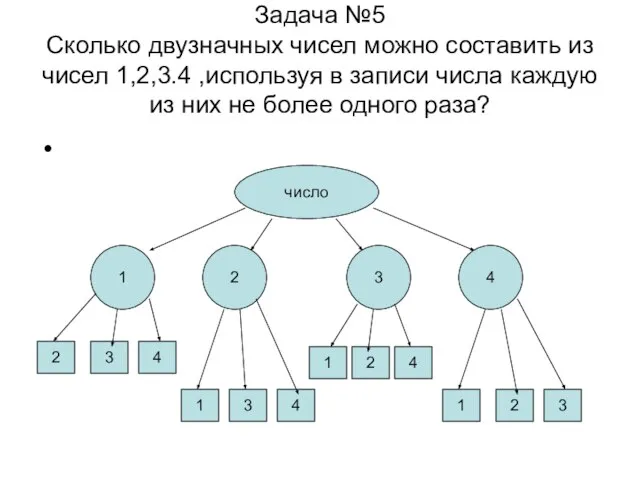
Слайд 11
Задача №5
Сколько двузначных чисел можно составить из
чисел 1,2,3.4 ,используя
в записи числа каждую из них не более одного
раза? •
число 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3
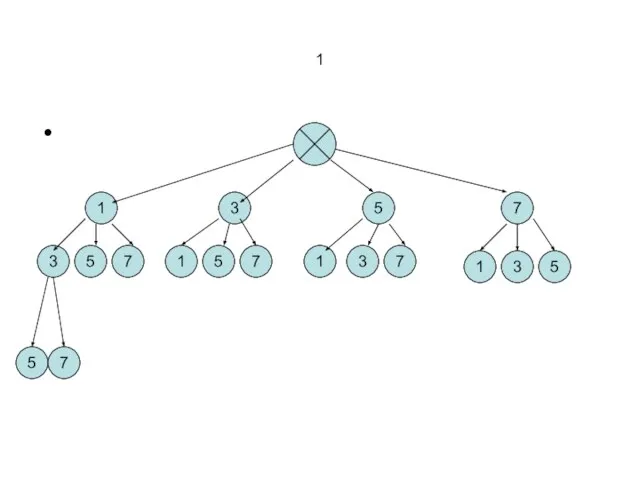
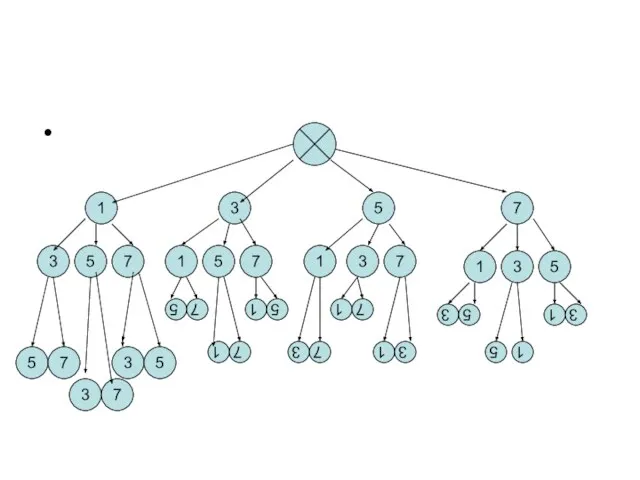
Слайд 12
Задача №
Сколько трёхзначных чисел можно составить из
цифр 1,3,5,7, используя
в записи числа каждую из них не более одного
раза?
Слайд 13
•
1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7
Слайд 14
•
1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7 3 7 3 5 75 1 7 1 5 3 7 1 7 1 3 3 5 5 1 1 3
Слайд 15
Задача №
Сколько трёхзначных чисел можно записать из
цифр 1,2,3 при
условии ,что 1)цифры в записи числа должны быть различны;2)цифры
в записи числа могут повторяться?•
Слайд 16
Задача №(устно)
Сколькими способами Петя и Вова могут занять
места за двухместной партой? • Сколькими способами вы можете
рассадить 3-х гостей на 3-х разноцветных табуретках. • № . Сколькими способами
вы можете рассадить 4-х гостей на 4-х разноцветных табуретках? • № .Сколькими способами вы можете рассадить 5-х гостей на 5-х разноцветных табуретках?
Слайд 17
«Правило произведения».
•
Если существует n вариантов выбора
первого элемента и для
каждого из них есть m вариантов выбора второго элемента,то
всего существует nxm различных пар с выбранными первым и вторым
элементами.
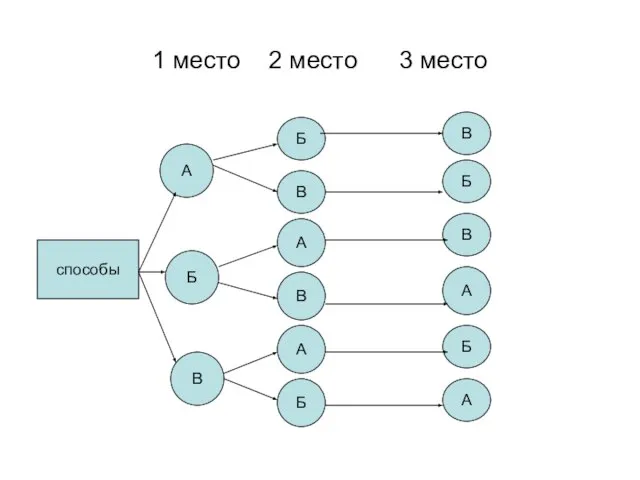
Слайд 18
Задача №
•
№ .Антон, Борис и Василий купили 3
билета
на 1-е,2-е и 3-е места первого ряда на футбольный
матч. Сколькими способами они могут занять имеющиеся места?
Слайд 19
1 место 2 место 3 место
способы А Б В Б В А В А Б В Б В А Б А
Слайд 20
Задача №
•
№ .В пятницу у вас 4 уроков: алгебра,
русский,
физика, история. Сколькими способами можно составить расписание на пятницу?
Слайд 21
А
Р
Ф
И
Р
Ф
Ф
ФФ Ф
Ф
Чтобы скачать презентацию - поделитесь ей с друзьями с помощью
социальных кнопок.
