Координатный метод

Содержание
Координаты точки
Расстояние между точками
Уравнение окружности
Координаты середины отрезка
Уравнение прямой
Заключение

Координаты точки
Говорят, что на плоскости задана прямоугольная система координат, если через некоторую точку О плоскости проведены две взаимно перпендикулярные прямые, на каждой из которых выбрано направление (которое на рисунке отмечается стрелкой) и одна и та же единица измерения отрезков. Точка O называется началом координат, а прямые с выбранными на них направлениями – осями координат. Одна из осей координат называется осью абсцисс, а другая – осью ординат. Ось абсцисс обозначается Ox, а ось ординат – Oy.
x
y
O
1
1
Прямоугольная система координат:
O – начало;
Ox – ось абсцисс;
Oy – ось ординат;
Ox ┴ Oy
на осях выбран масштаб (единичный отрезок)

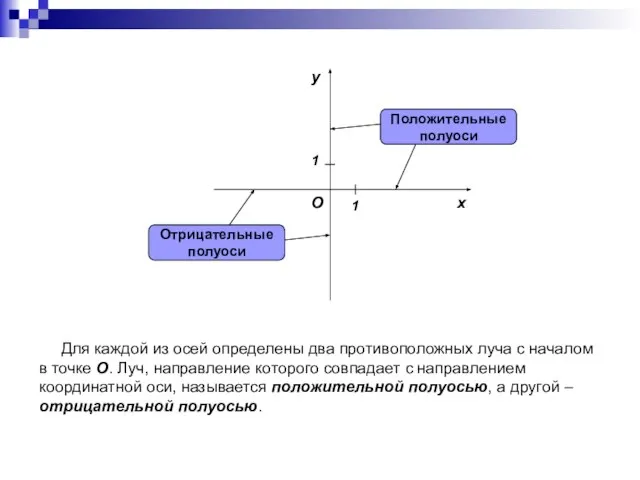
Для каждой из осей определены два противоположных луча с началом в точке O. Луч, направление которого совпадает с направлением координатной оси, называется положительной полуосью, а другой – отрицательной полуосью.
x
y
O
Положительные
полуоси
Отрицательные
полуоси
1
1

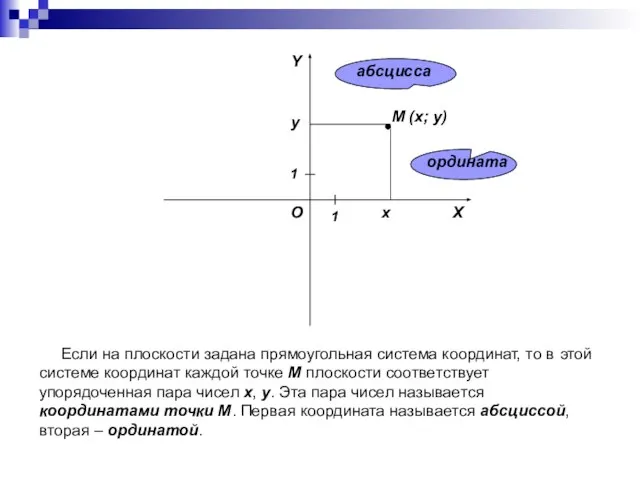
Если на плоскости задана прямоугольная система координат, то в этой системе координат каждой точке M плоскости соответствует упорядоченная пара чисел x, y. Эта пара чисел называется координатами точки M. Первая координата называется абсциссой, вторая – ординатой.
x
y
O
1
1
M (x; y)
X
Y
абсцисса
ордината

Пусть M1 и M2 – точки пересечения осей координат Ox и Oy с прямыми, проходящими перпендикулярно им через точку M соответственно. Тогда координаты x, y точки M определяются следующим образом:
x = OM1, если точка M1 принадлежит положительной полуоси;
x = 0, если M1 совпадает с точкой O;
x = – OM1, если точка M1 принадлежит отрицательной полуоси;
y = OM2 , если M2 принадлежит положительной полуоси;
y = 0, если M2 совпадает с точкой О;
y = – OM , если точка M2 принадлежит отрицательной полуоси.
x
y
O
1
1
M
M1
M2

Координаты точки M записываются в скобках после обозначения точки: M (x; y) (на первом месте записывается абсцисса, на втором записывается ордината).
Если точка M лежит на оси Ox, то она имеет координаты (x; 0), если M лежит на оси Oy, то ее координаты – (0; y).
x
y
O
M (x; 0)
M (0; y)
x
y
O
1
1
1
1

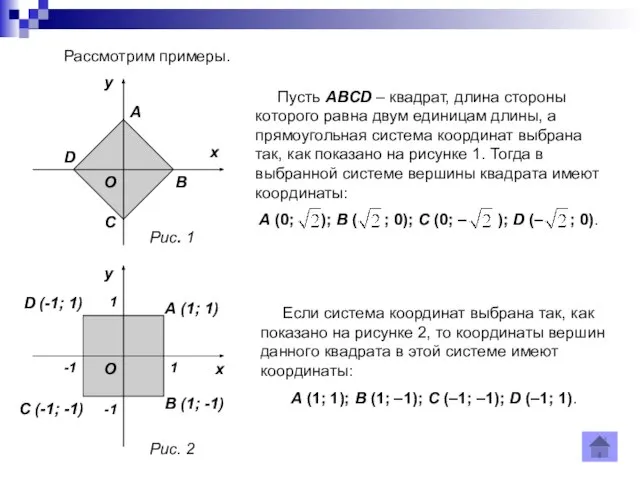
Рассмотрим примеры.
Пусть ABCD – квадрат, длина стороны которого равна двум единицам длины, а прямоугольная система координат выбрана так, как показано на рисунке 1. Тогда в выбранной системе вершины квадрата имеют координаты:
A (0; ); B ( ; 0); C (0; – ); D (– ; 0).
Если система координат выбрана так, как показано на рисунке 2, то координаты вершин данного квадрата в этой системе имеют координаты:
A (1; 1); B (1; –1); C (–1; –1); D (–1; 1).
x
y
O
A
B
C
D
1
1
-1
-1
x
y
O
A (1; 1)
B (1; -1)
C (-1; -1)
D (-1; 1)
Рис. 1
Рис. 2

Рассмотрим вопрос о нахождении расстояния между точками, если известны их координаты. Пусть на плоскости выбрана прямоугольная система координат и известны координаты точек A и B в этой системе координат: A (x1; y1) и B (x2; y2). Тогда расстояние d (A, B) = AB между точками A и B можно найти по формуле
x
y
O
A (x1; y1)
B (x2; y2)
x1
x2
y1
y2
Расстояние между точками

Докажем формулу для случая, когда и , т. е. когда отрезок AB не параллелен ни одной из координатных осей. Пусть C – точка пересечения прямых l1 и l2, которые проходят через точки A, B соответственно и параллельны осям Oy, Ox. Рассмотрим прямоугольный треугольник ABC. Длины сторон AC и BC равны: AC = , BC = . Тогда по теореме
Пифагора
или
x
y
O
l1
l2
A
B
C

Заметим, что формула верна и для случаев:
а) х1 = х2, y1 y2 (отрезок параллелен оси Oy, рисунок 1);
б) х1 х2, у1 = у2 (отрезок параллелен оси Ox, рисунок 2);
в) х1 = х2, у1 = у2 (точки A и B совпадают).
В случае а) d (A, B) = AB = .
В случае б) d (A, B) = AB = .
Если точки A и B совпадают, то d (A, B) = 0.
x
y
O
x
y1
y2
A (x; y1)
B (x; y2)
x
y
O
A (x1; y)
B (x2; y)
x1
x2
Рис. 1
Рис. 2

Рассмотрим пример.
Пусть необходимо вычислить площадь квадрата ABCD, две вершины которого имеют координаты A (8; 8) и B (5; 5). Площадь квадрата равна квадрату длины стороны.
Следовательно, SABCD = AB² . Для вычисления длины стороны AB воспользуемся формулой расстояния между двумя точками
Таким образом, площадь квадрата SABCD = AB = 18 кв. ед.
Ответ: 18 кв. ед.

Уравнение окружности
Рассмотрим вопрос об уравнении
окружности.
Уравнение с двумя переменными называется уравнением фигуры, если ему удовлетворяют координаты любой точки этой фигуры и не удовлетворяют координаты точек, не принадлежащих данной фигуре.
Составим уравнение окружности с центром в точке O (x0; y0) и радиусом R.
Пусть точка M (x; y) принадлежит окружности. Тогда в силу определения окружности СM = R. Следовательно, квадрат расстояния между точками С и M равен квадрату радиуса:
(x – x0)2 + (y – y0)2 = R2 .
x
y
O
C
x0
y0
M (x; y)

Пусть точка M1 (x1; y1) не принадлежит окружности, тогда СM1 ≠ R, а значит, (x – x1)2 + (у – у1)2 ≠ R2, т. е. если точка не принадлежит окружности, то еe координаты не удовлетворяют уравнению
(x – x0)2 + (у – у0)2 = R2 .
Таким образом, уравнение
(x – x0)2 + (у – у0)2 = R2
есть уравнение окружности с центром в точке С (x0; y0) и радиусом R.
Заметим, что если центр окружности совпадает с началом системы координат, то уравнение окружности имеет вид
x2 + y2 = R2 .
x
y
O
R

Задача. Составьте уравнение фигуры на плоскости, состоящей из всех точек, сумма квадратов расстояний которых от точек A (–6; 0)
и B (6; 0) равна 104.
Решение.
x
y
O
A
B
M
1) Пусть M (x; y) – точка, принадлежащая фигуре, уравнение которой необходимо составить. Тогда по условию задачи AM2 + BM2 = 104.
2) Воспользуемся формулой для нахождения расстояния между точками, координаты которых известны. Получаем:
3) По условию задачи (x + 6)2 + y2 + (x – 6)2 + y2 = 104. После упрощения получаем x2 + y2 = 16.
Если точка M (x; y) не принадлежит фигуре, о которой идет речь в задаче, то AM2 + BM2 ≠ 104, а значит, координаты точки M (x; y) не удовлетворяют уравнению x2 + y2 = 16. Таким образом, уравнение фигуры имеет вид x2 + y2 = 16 и фигура является окружностью с центром в начале координат и радиусом 4.

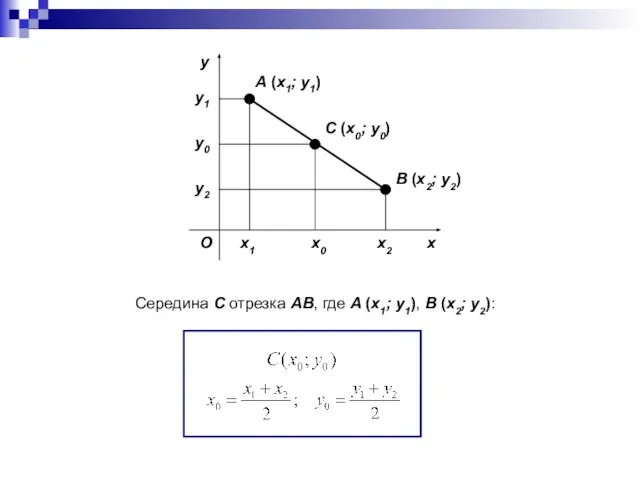
Координаты середины отрезка
Рассмотрим вопрос о вычислении координат середины отрезка, если известны координаты концов этого отрезка.
Пусть A (x1; y1) и B (x2; y2) – произвольные точки плоскости, а точка C (x0; y0) – середина отрезка AB. Найдем координаты х0 и y0.
Найдем координату x0.
1) Пусть отрезок AB не параллелен оси Oy, т. е. x1 ≠ x2. Проведем через точки A, B и C прямые, параллельные оси Oy, которые пересекают ось Ox в точках A1 (x1; 0), B1 (x2; 0) и C0 (x0; 0) соответственно. Тогда по теореме Фалеса точка C0 (x0; 0) – середина отрезка A1B1, т. е. A1C0 = C0B1 или |x0 – x1| = |x0 – x2|. Отсюда следует, что либо x0 – x1 = x0 – x2, либо x0 – x1 = –(x0 – x2). Так как x1 ≠ x2, то первое равенство невозможно, а значит, верно второе равенство, из которого получаем, что
x
y
O
A
B
C
A1
B1
C0

2) Пусть отрезок AB параллелен оси Oy, т. е. x1 = x2. В этом случае все точки A1, B1, C0 имеют одну и ту же абсциссу, а следовательно, формула
верна и в этом случае (рис. 1).
Координата y0 точки C0 находится аналогично. В этом случае рассматриваются прямые, параллельные оси Oх (рис. 2), а соответствующая формула имеет вид
x
y
O
A
B
C
x
y
O
A
B
C
Рис. 1
Рис. 2

x
y
O
A (x1; y1)
B (x2; y2)
C (x0; y0)
x1
x2
y1
y2
Середина C отрезка AB, где A (x1; y1), B (x2; y2):
x0
y0

Задача. Концами отрезка служат точки A (–8; –5), B (10; 4). Найдите координаты точек C и D, которые делят отрезок AB на три равные части.
Решение.
Пусть точки C и D имеют координаты (xC; yC) и (xD; yD).
1) Найдем абсциссы точек C и D.
Так как точка C – середина отрезка AD, то выполняется равенство
так как точка D – середина отрезка CB, то
Решив систему 2xC = xD – 8,
2xD = 10 + xC ,
находим xC = –2, xD = 4.

2) Найдем ординаты точек С и D.
Для нахождения ординат точек С и D воспользуемся равенствами
Решив систему
2yC = yD – 5,
2yD = yC + 4,
находим yC = –2, yD = 1.
Ответ: C (–2; –2), D (4; 1).

Уравнение прямой
Выведем уравнение прямой, проходящей через две точки, координаты которых известны. Пусть на плоскости дана прямая l и выбрана прямоугольная система координат. Рассмотрим две различные точки A (x1; y1) и B (x2; y2) такие, что прямая l является серединным перпендикуляром для отрезка AB.
1) Если точка M (x; y) лежит на прямой l, то AM = BM. Следовательно, координаты точки M удовлетворяют уравнению
(x – x1)2 + (y – y1)2 = (x – x2)2 + (y – y2)2,
которое после преобразования принимает вид
ax + by + c = 0,
где a = 2(x1 – x2), b = 2(y1 – y2), c = x22 + y22 – x12 – y12. Заметим, что хотя бы один из коэффициентов a, b уравнения ax + by + c = 0 не равен нулю, т. к. точки A и B различные, а значит, хотя бы одна из разностей x1 – x2, y1 – y2 не равна нулю.
Таким образом, если точка M лежит на прямой l, то ее координаты удовлетворяют уравнению ax + by + c = 0, где коэффициенты a и b одновременно не равны нулю.
x
y
O
l
A
B
M

2) Если точка M (x; y) не лежит на прямой l, то AM ≠ BM и AM2 ≠ BM2, а следовательно, координаты точки M не удовлетворяют уравнению ax + by + c = 0.
Таким образом, уравнением прямой в прямоугольной системе
координат является уравнение первой степени
ax + by + c = 0 ,
где a и b одновременно не равны нулю.
x
y
O
A
B
M
l
Если a = 0, то y = c1 – прямая || Ox.
Если b = 0, то y = c2 – прямая || Oy.
Если с = 0, то прямая проходит через O (0; 0).

Задача. Дан равнобедренный прямоугольный треугольник ACB с
прямым углом при вершине C. Найдите множество точек M плоскости, для каждой из которых выполняется условие AM2 + BM2 = 2CM2.
Решение.
Рассмотрим систему координат, начало которой совпадает с вершиной C, а вершины A и B расположены на осях Ox и Oy, как показано на рисунке. Если катет данного треугольника равен a, тогда (0; 0), (a; 0), (0; a) – координаты точек C, A и B в выбранной системе координат соответственно. Пусть (x; y) – координаты точки M, принадлежащей искомому множеству точек.
x
y
C
A
B

Воспользуемся формулой для нахождения расстояния между точками, если известны их координаты:
По условию задачи AM2 + BM2 = 2CM2, следовательно,
(x – a)2 + y2 + x2 + (y – a)2 = 2(x2 + y2).
Отсюда получаем уравнение x + y – a = 0.
Если точка M (x; y) не принадлежит искомому множеству точек, то
AM2 + BM2 ≠ 2CM2, а значит, координаты точки M не удовлетворяют
уравнению x + y – a = 0. Таким образом, x + y – a = 0 есть уравнение
искомого множества точек и это множество есть прямая, на которой
лежит гипотенуза AB данного треугольника.