Содержание
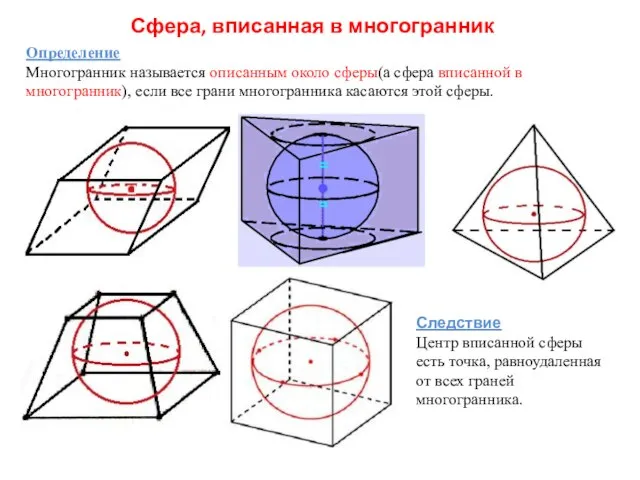
- 2. Сфера, вписанная в многогранник Определение Многогранник называется описанным около сферы(а сфера вписанной в многогранник), если все
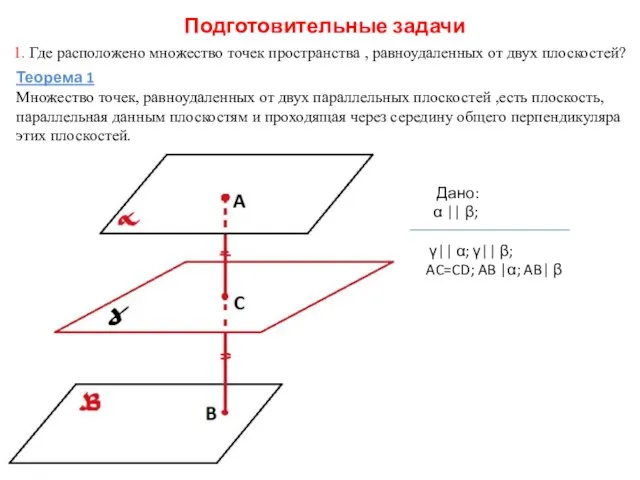
- 3. Подготовительные задачи 1. Где расположено множество точек пространства , равноудаленных от двух плоскостей? Теорема 1 Множество
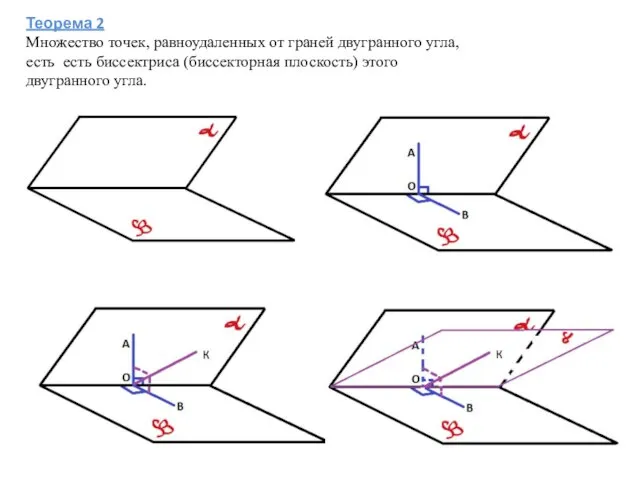
- 4. Теорема 2 Множество точек, равноудаленных от граней двугранного угла, есть есть биссектриса (биссекторная плоскость) этого двугранного
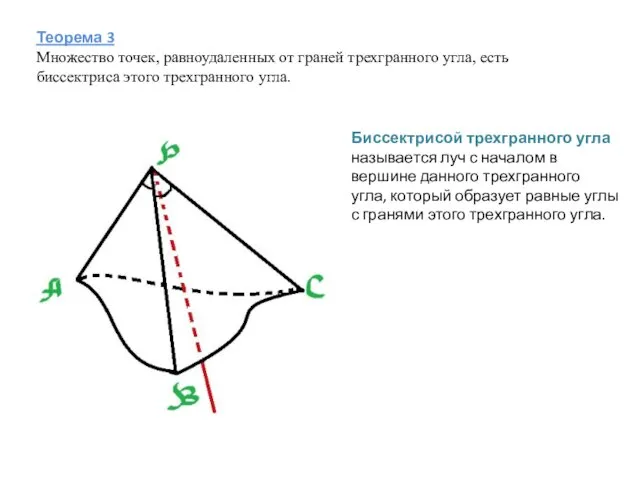
- 5. Теорема 3 Множество точек, равноудаленных от граней трехгранного угла, есть биссектриса этого трехгранного угла. Биссектрисой трехгранного
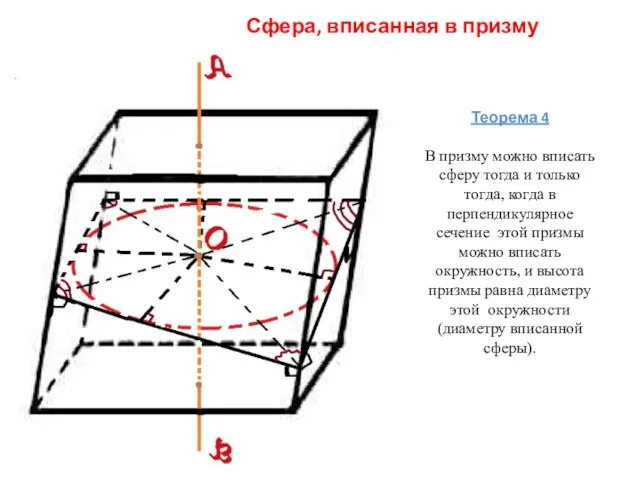
- 6. Сфера, вписанная в призму Теорема 4 В призму можно вписать сферу тогда и только тогда, когда
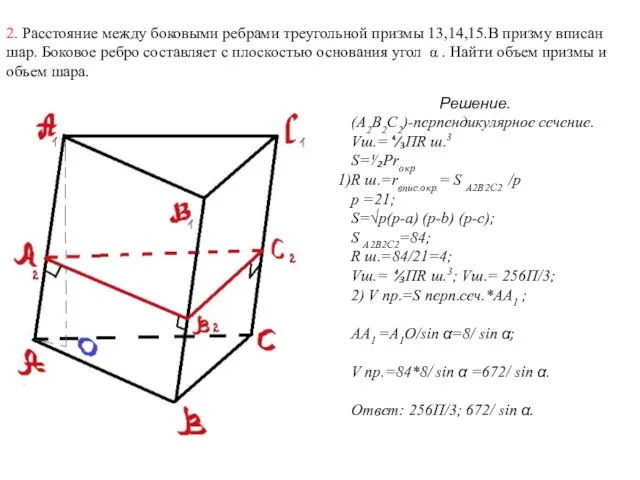
- 7. 2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В призму вписан шар. Боковое ребро составляет с плоскостью
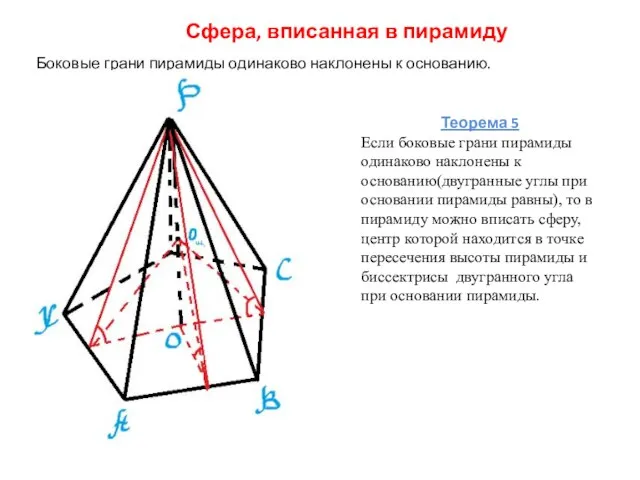
- 8. Сфера, вписанная в пирамиду Боковые грани пирамиды одинаково наклонены к основанию. Теорема 5 Если боковые грани
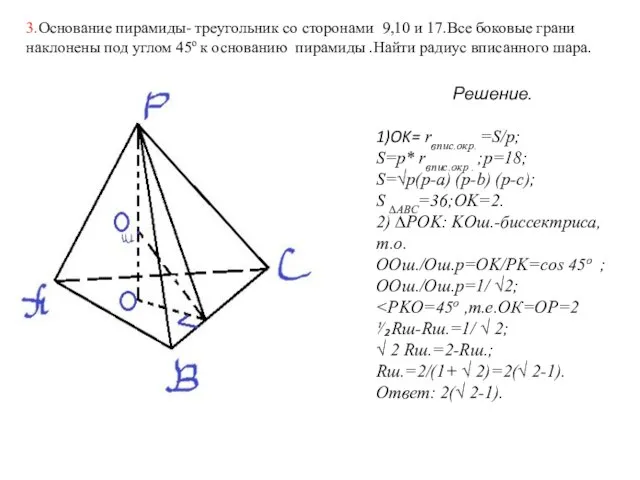
- 9. 3.Основание пирамиды- треугольник со сторонами 9,10 и 17.Все боковые грани наклонены под углом 45о к основанию
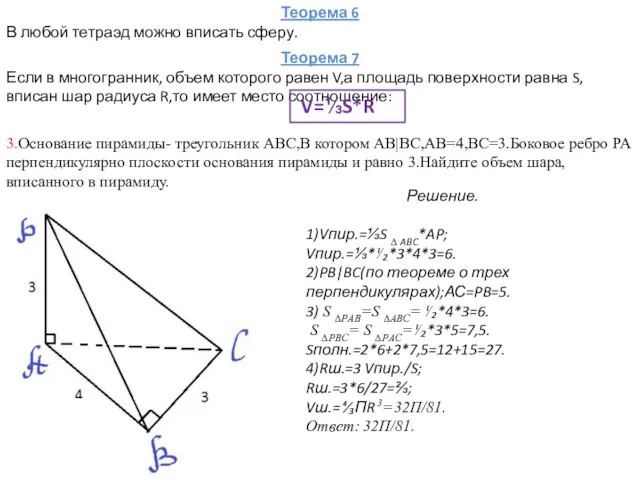
- 10. Теорема 6 В любой тетраэд можно вписать сферу. Теорема 7 Если в многогранник, объем которого равен
- 11. 4. Шар вписан в прямую призму, основание которой- равнобедренная трапеция с основаниями 2 и 8.Найдите объем
- 13. Скачать презентацию

 ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Треугольник Устные задачи
Треугольник Устные задачи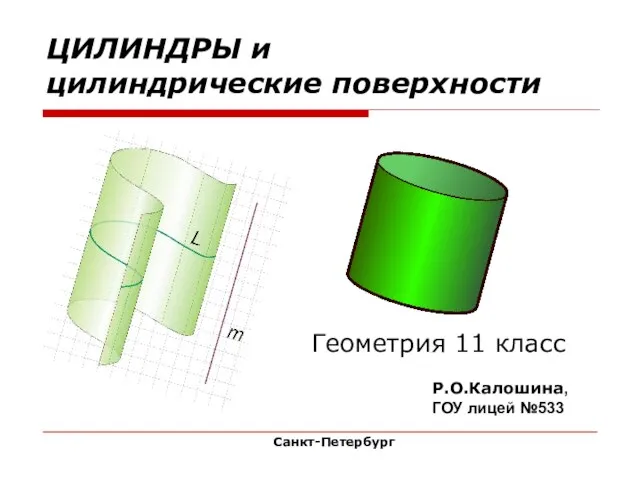 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Параллелограмм
Параллелограмм Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Правильная пирамида
Правильная пирамида Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Задания на клетчатой бумаге
Задания на клетчатой бумаге Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Амидекстр
Амидекстр Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Геометрия Лобачевского
Геометрия Лобачевского Геометрические задачи на экстремум
Геометрические задачи на экстремум Биссектриса угла
Биссектриса угла Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Пирамиды
Пирамиды Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Понятие цилиндра
Понятие цилиндра Перпендикуляр и наклонная
Перпендикуляр и наклонная Лист Мёбиуса
Лист Мёбиуса Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости