Содержание
- 2. Цель урока: ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов равнобедренного треугольника; научиться
- 3. Отгадайте ребус Треугольник
- 4. Из трёх точек состоит из века в век, Потому что так придумал человек. Не лежат при
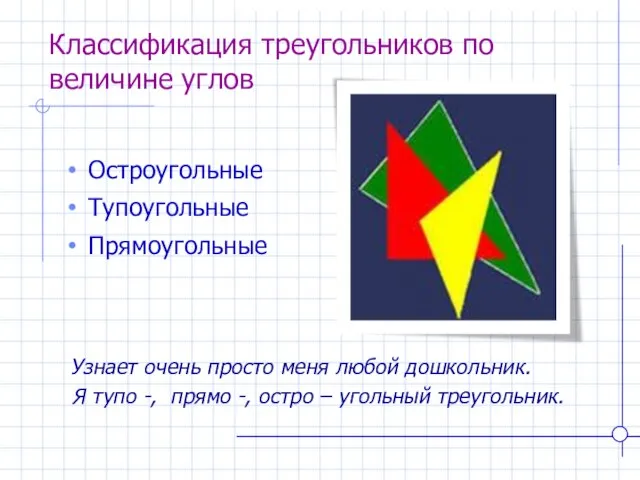
- 5. Классификация треугольников по величине углов Узнает очень просто меня любой дошкольник. Я тупо -, прямо -,
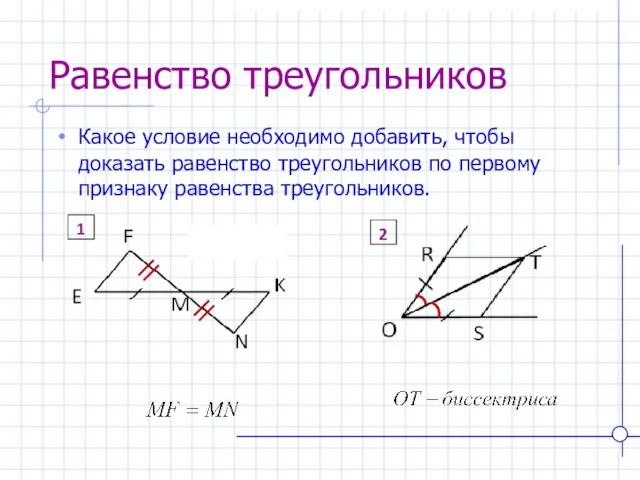
- 6. Равенство треугольников Какое условие необходимо добавить, чтобы доказать равенство треугольников по первому признаку равенства треугольников. 2
- 7. Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал ещё в
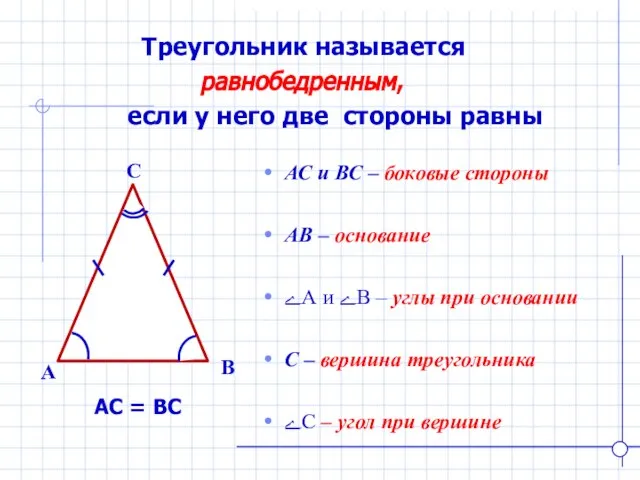
- 8. Треугольник называется равнобедренным, если у него две стороны равны B A C АС и ВС –
- 9. Равнобедренный треугольник В равнобедренном треугольнике АМК АМ = АК. Назовите основание и углы при основании этого
- 10. Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему? У равнобедренных треугольников назовите: боковые стороны, основание,
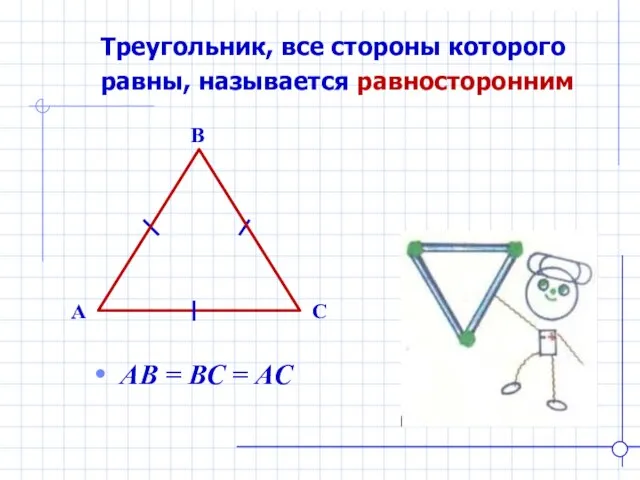
- 11. Треугольник, все стороны которого равны, называется равносторонним B A C АВ = ВС = АС
- 12. Зовусь я треугольник, Со мной хлопот не оберётся школьник … По – разному всегда я называюсь,
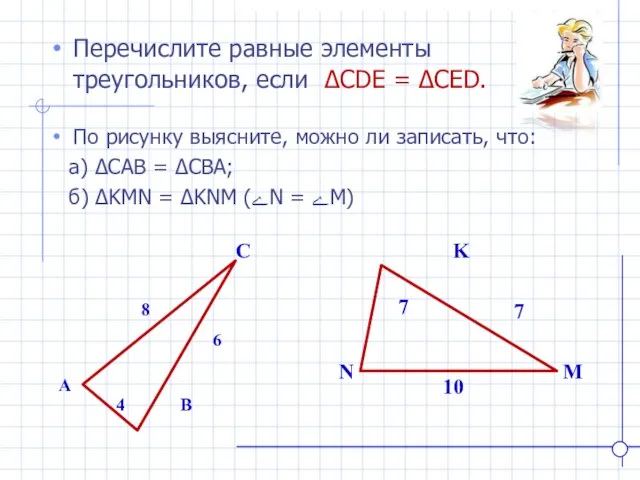
- 13. K N M Перечислите равные элементы треугольников, если ∆CDE = ∆CED. A B C 4 8
- 14. Теорема. В равнобедренном треугольнике углы при основании равны. Дано: ∆ABC, CA = CB. Доказать: в ∆
- 15. Решение задач В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника. В
- 16. Решение задач Найдите угол KBA. ےKBA = 70° ےKBA = 40° ےKBA = 110° 1 2
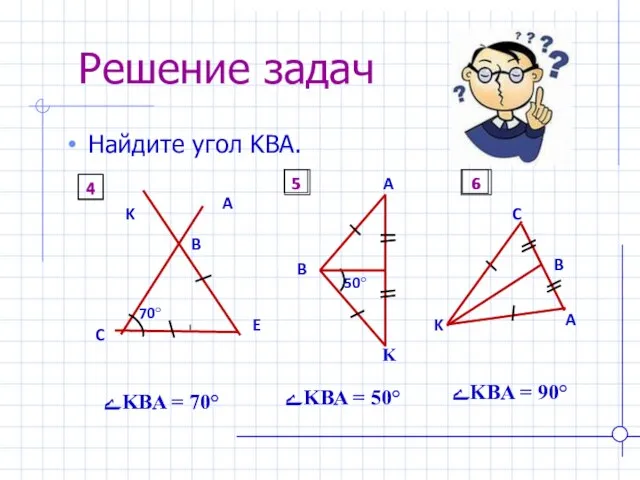
- 17. Решение задач Найдите угол KBA. ےKBA = 70° ےKBA = 50° ےKBA = 90° 4 5
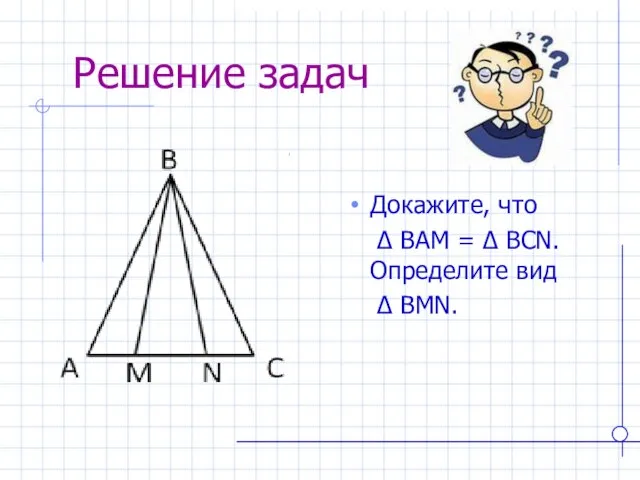
- 18. Решение задач Докажите, что ∆ BAM = ∆ BCN. Определите вид ∆ BMN.
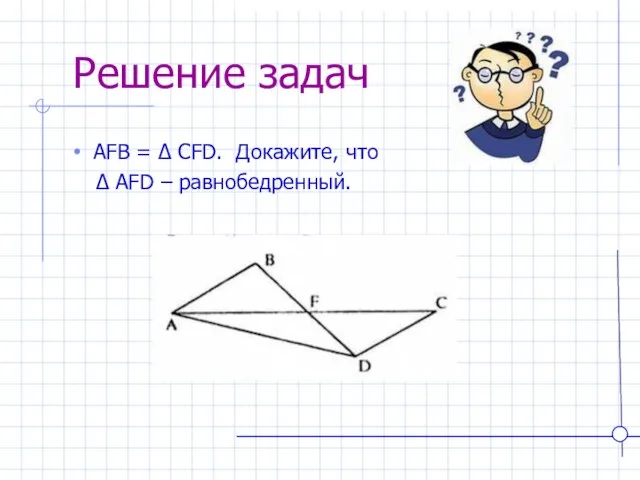
- 19. Решение задач AFB = ∆ CFD. Докажите, что ∆ AFD – равнобедренный.
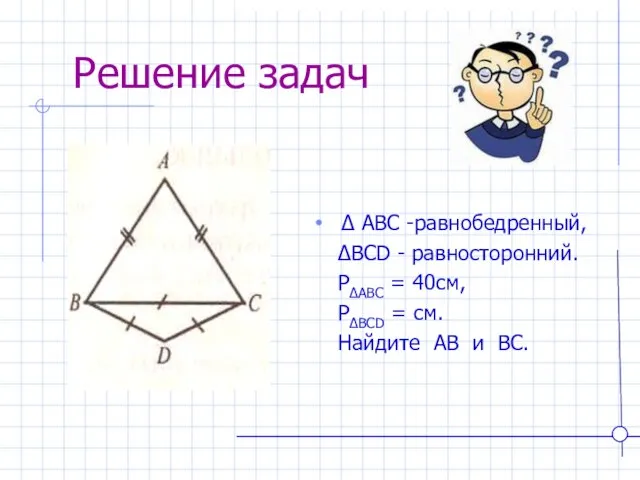
- 20. Решение задач ∆ ABC -равнобедренный, ∆BCD - равносторонний. P∆ABC = 40см, P∆BCD = см. Найдите AB
- 21. Контрольные вопросы Какой треугольник называется равнобедренным? Какой треугольник называется равносторонним? Является ли равносторонний треугольник равнобедренным? Каким
- 22. Домашнее задание Изучить п. 23. Контрольные вопросы 3 – 5 на стр. 37. Выполнить упр. 9,
- 23. Удачи!
- 25. Скачать презентацию












 Окружности
Окружности Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Площадь трапеции
Площадь трапеции Объемные тела. Пирамиды
Объемные тела. Пирамиды Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Аксиомы стереометрии Решение задач
Аксиомы стереометрии Решение задач Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач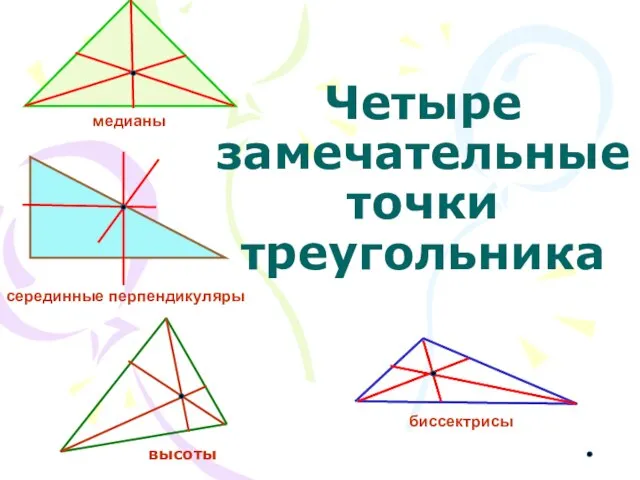 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Замечательные кривые
Замечательные кривые Вокруг храма с линейкой и циркулем
Вокруг храма с линейкой и циркулем Фракталы: наука и искусство XXI века
Фракталы: наука и искусство XXI века Сечения пространственных фигур
Сечения пространственных фигур Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности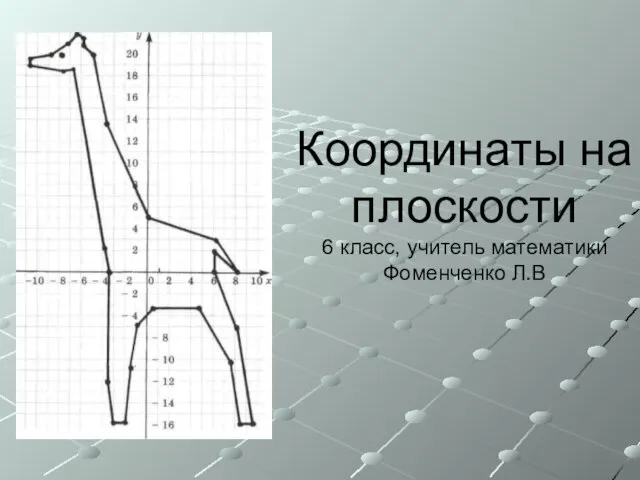 Координаты на плоскости
Координаты на плоскости Чертёж группы геометрических тел.
Чертёж группы геометрических тел. Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Магические квадраты (6 класс)
Магические квадраты (6 класс) Сравнение величин углов. Классификация углов по градусной мере
Сравнение величин углов. Классификация углов по градусной мере Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Описанная окружность
Описанная окружность Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Умножение вектора на число
Умножение вектора на число Прямоугольный треугольник
Прямоугольный треугольник Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Магические квадраты
Магические квадраты Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья
Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья  Треугольники. Третий признак равенства
Треугольники. Третий признак равенства