Содержание
- 2. Выполнила: Жубанова Диана ученица 7 класса Карасаевской СОШ
- 3. Цель исследования: Изучить круги Эйлера Научиться применять данный способ для решения задач Cоставлять задачи практического содержания.
- 4. Немного об истории Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению
- 5. Немного об истории Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843
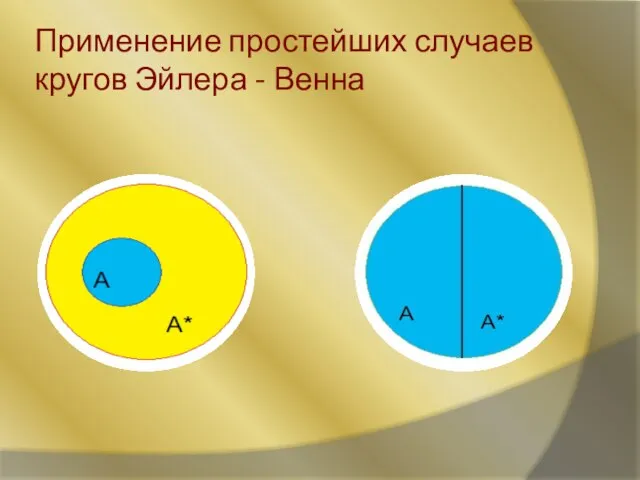
- 6. Применение простейших случаев кругов Эйлера - Венна
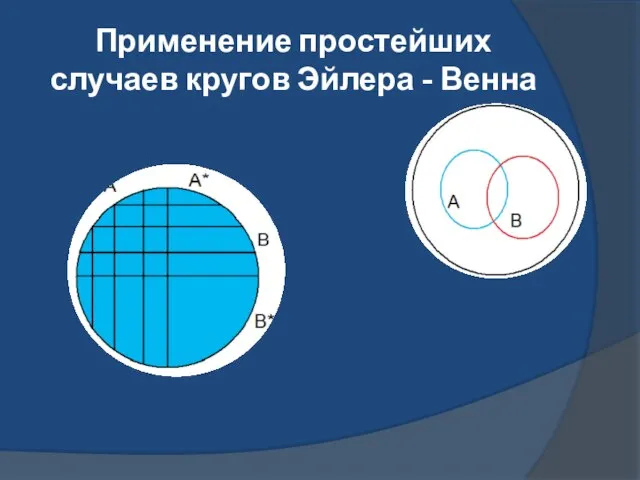
- 7. Применение простейших случаев кругов Эйлера - Венна
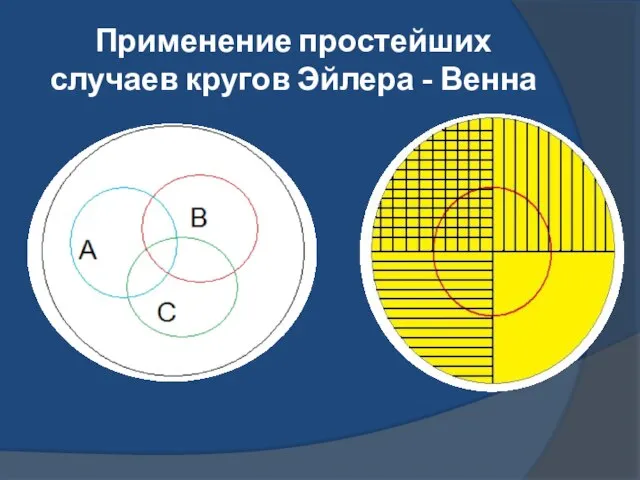
- 8. Применение простейших случаев кругов Эйлера - Венна
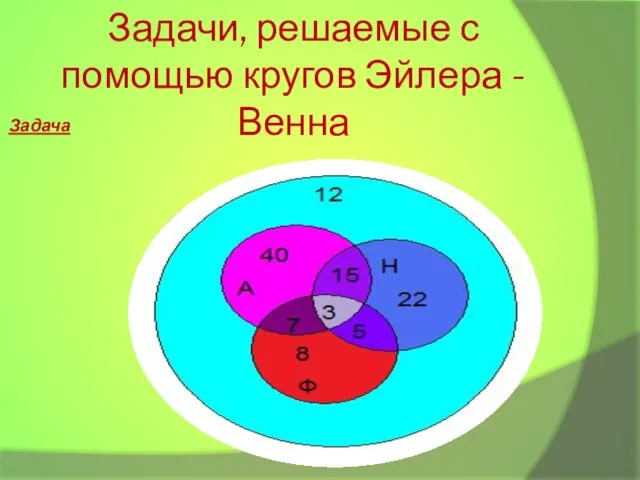
- 9. Задачи, решаемые с помощью кругов Эйлера - Венна Задача
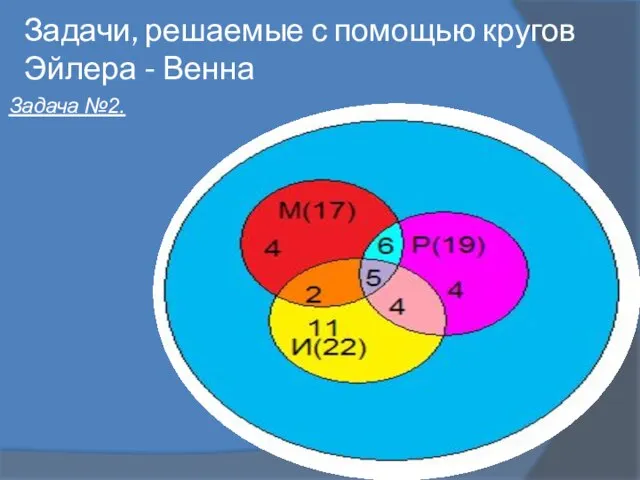
- 10. Задачи, решаемые с помощью кругов Эйлера - Венна Задача №2.
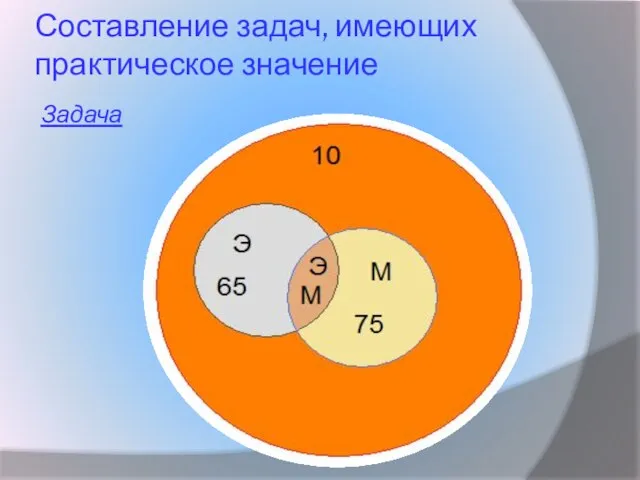
- 11. Составление задач, имеющих практическое значение Задача
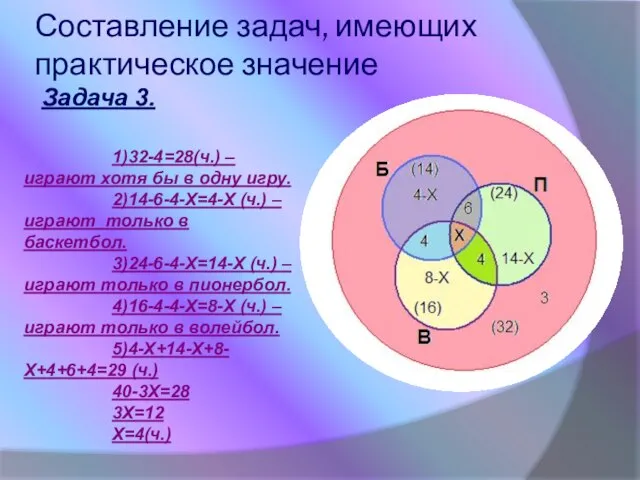
- 12. Составление задач, имеющих практическое значение Задача 3. 1)32-4=28(ч.) – играют хотя бы в одну игру. 2)14-6-4-Х=4-Х
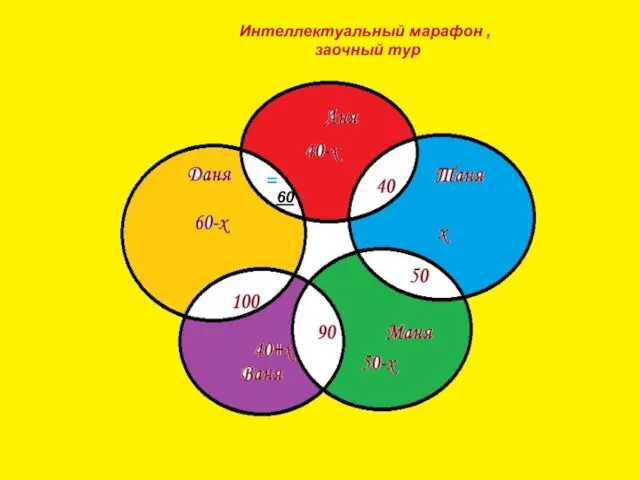
- 13. Интеллектуальный марафон , заочный тур 60
- 14. Ты человек, а значит, ты Обязан рассуждать – А без логичной простоты Ты будешь пропадать. Пусть
- 15. Алгоритм решения задач с помощью кругов Эйлера - Венна Заключение Записываем краткое условие задачи. Выполняем рисунок.
- 17. Скачать презентацию






 Объём призмы
Объём призмы Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Объем конуса
Объем конуса Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Объём пирамиды
Объём пирамиды Шар. Сфера
Шар. Сфера Понятие движения
Понятие движения Первый признак равенства треугольников
Первый признак равенства треугольников Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А.
Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А. Вводное повторение курса геометрии
Вводное повторение курса геометрии Площади и объемы
Площади и объемы Прямоугольные треугольники 7 класс
Прямоугольные треугольники 7 класс Координатный метод
Координатный метод Геометрия Лобачевского
Геометрия Лобачевского Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ Геометрия. Как она возникла?
Геометрия. Как она возникла? Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах. Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн
Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн Двугранные углы
Двугранные углы Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Площади фигур. Зачёт
Площади фигур. Зачёт Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ Окружности
Окружности Трехгранный угол
Трехгранный угол Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Геометрические построения на плоскости
Геометрические построения на плоскости