Содержание
Слайд 2=x0+∆x
Приращение функции и приращение аргумента
y=f(x)
x0
f(x)=f(x0+∆x)
f(x0)
∆x
∆f
приращение аргумента:
x
y
∆х = х - х0 (1)
Приращение функции
=x0+∆x
Приращение функции и приращение аргумента
y=f(x)
x0
f(x)=f(x0+∆x)
f(x0)
∆x
∆f
приращение аргумента:
x
y
∆х = х - х0 (1)
Приращение функции
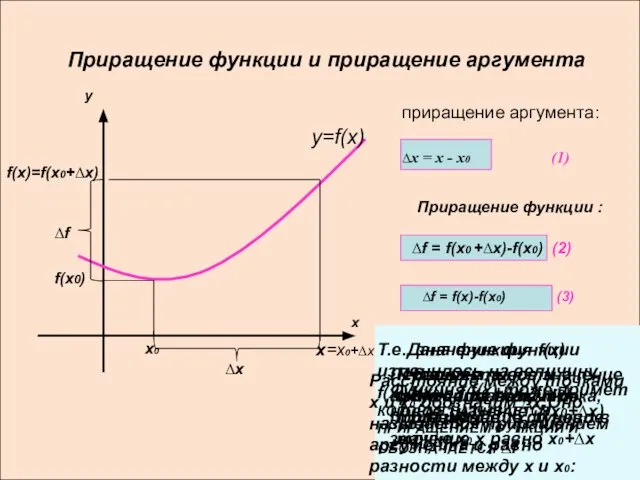
:
∆f = f(x0 +∆x)-f(x0) (2)
∆f = f(x)-f(x0) (3)
x
В окрестности точки х0 возьмём точку х
Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0
Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:
Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х
Функция f(х) тоже примет новое значение: f(x0+∆x)
Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f
Дана функция f(x)
- Предыдущая
ВетерСледующая -
Геометрия.Введение. Аксиоматика. Объёмы и поверхности тел вращения
Объёмы и поверхности тел вращения Измеряем длину окружности
Измеряем длину окружности Многогранник
Многогранник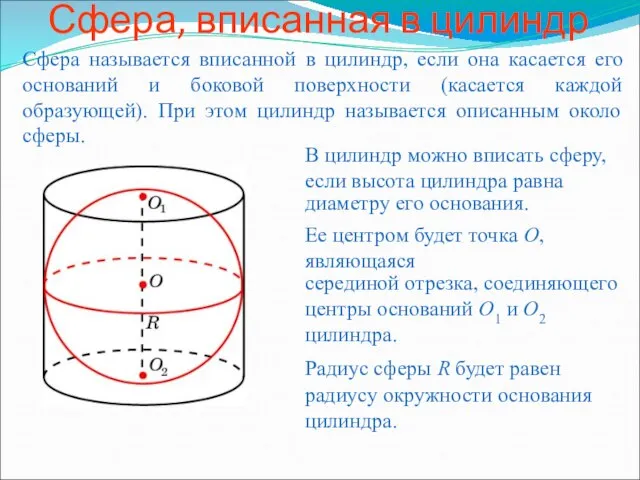 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Треугольники. Третий признак равенства
Треугольники. Третий признак равенства Основные труды и биография Декарта
Основные труды и биография Декарта Периметр – сумма длин всех сторон.
Периметр – сумма длин всех сторон. Равнобедренный треугольник
Равнобедренный треугольник Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Второй признак равенства треугольников
Второй признак равенства треугольников Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Введение в стереометрию
Введение в стереометрию Длина отрезка
Длина отрезка Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Площадь параллелограмма и треугольника
Площадь параллелограмма и треугольника Угол между плоскостями
Угол между плоскостями Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии
Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии Окружности
Окружности Амидекстр
Амидекстр Графы и их применение
Графы и их применение Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Сечения
Сечения Перпендикулярные прямые 7 класс
Перпендикулярные прямые 7 класс Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Магические квадраты (6 класс)
Магические квадраты (6 класс)