Содержание
- 2. Цель урока: Доказать теорему о теорему о соотношениях между сторонами и углами треугольника Научить применять теорему
- 3. План урока: Орг. Момент Устный опрос по теории Решите устно Объяснение нового материала Закрепление нового материала
- 4. Решите устно В △АВС А=37°, В=109°.Найдите величину С. Один из острых углов прямоугольного треугольника равен 32°.Какова
- 5. Решите устно 4. Вычислите углы равнобедренного треугольника, если угол при основании 77°. 5. Вычислите величины острых
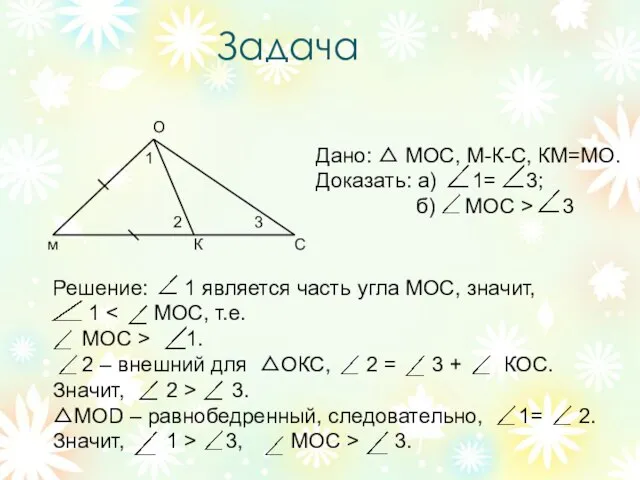
- 6. Задача м О С К 1 2 3 Дано: △ МОС, М-К-С, КМ=МО. Доказать: а) 1=
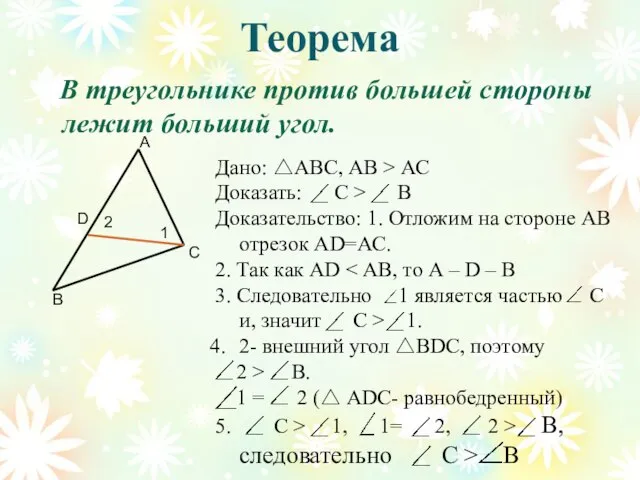
- 7. Теорема В треугольнике против большей стороны лежит больший угол. В С А Дано: △АВС, АВ >
- 8. Обратная теорема Против большего угла лежит большая сторона В А С Дано: △АВС, С > В
- 9. Решение задач № 236 и №237-устно № 238
- 11. Скачать презентацию






 Сферическая поверхность. Шар Геометрия 11 класс
Сферическая поверхность. Шар Геометрия 11 класс Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости Введение в стереометрию
Введение в стереометрию Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Круги Эйлера и их практическое применение
Круги Эйлера и их практическое применение Приготовьтесь к построению
Приготовьтесь к построению Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области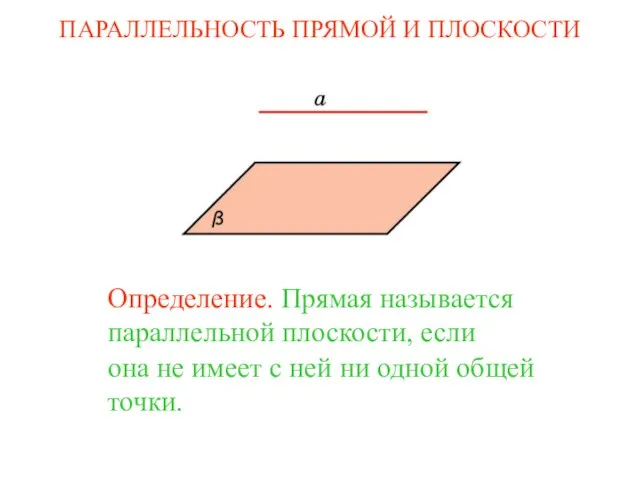 Параллельность прямой и плоскости
Параллельность прямой и плоскости Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Вокруг храма с линейкой и циркулем
Вокруг храма с линейкой и циркулем Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Виды углов. Измерение углов
Виды углов. Измерение углов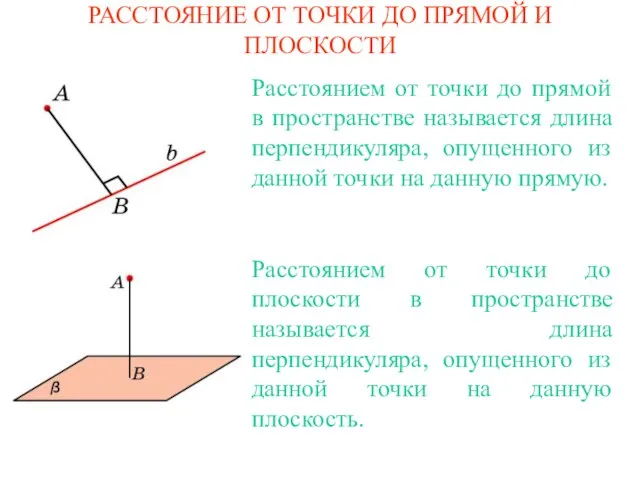 Расстояние от точки до прямой и плоскости
Расстояние от точки до прямой и плоскости Прямоугольник и его свойства
Прямоугольник и его свойства Пирамиды
Пирамиды Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Координатный метод
Координатный метод Приращение функции и приращение аргумента
Приращение функции и приращение аргумента Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Решение прямоугольных треугольников
Решение прямоугольных треугольников Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Первый признак равенства треугольников
Первый признак равенства треугольников Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Смежные и вертикальные углы
Смежные и вертикальные углы вид разреза сечения
вид разреза сечения Секреты квадрата и кубика
Секреты квадрата и кубика