Слайд 2Обобщающий урок
по теме
"Площади"

Слайд 3Является утверждение верным или неверным
1) Если 2 многоугольника имеют равные площади,

то они равны
Слайд 4Является утверждение
верным или неверным
2)Если многоугольник составлен из нескольких многоугольников, то

его площадь равна сумме площадей этих многоугольников
Слайд 5Является утверждение
верным или неверным
3)Квадратный сантиметр – это фигура, стороны которой равны

1см
Слайд 6Является утверждение
верным или неверным
4) Площадь квадрата равна произведению его сторон

Слайд 7Является утверждение
верным или неверным
5)Площадь треугольника равна произведению стороны на высоту, проведённую

к этой стороне
Слайд 8Является утверждение
верным или неверным
6) Площадь параллелограмма равна произведению стороны параллелограмма на

высоту
Слайд 9Является утверждение
верным или неверным
7) Площадь прямоугольного треугольника равна половине произведения катетов

Слайд 10Является утверждение
верным или неверным
8) Площадь трапеции равна произведению суммы оснований на

половину высоты
Слайд 11Является утверждение
верным или неверным
9) Теорема Пифагора гласит: Если квадрат одной стороны

треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
Слайд 12Является утверждение
верным или неверным
10) Если угол одного треугольника равен углу другого

треугольника, то площади этих треугольников относятся как произведения сторон , заключающих равные углы
Слайд 13Выберите номер верного утверждения

Слайд 1411) Высотой трапеции называется:
перпендикуляр, проведённый к её основанию
отрезок, пересекающий основание под прямым

углом
перпендикуляр, опущенный из вершины трапеции
перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
Слайд 1512) Если высоты треугольников равны, то:
их площади равны
их площади относятся как основания
эти

треугольники равны
основания к которым они проведены, равны
Слайд 1613) Египетским треугольником называют такой треугольник, длины сторон которого:
удовлетворяют теореме Пифагора
удовлетворяют, обратной

теореме Пифагора
равны 3,4 и 5
равны целым числам
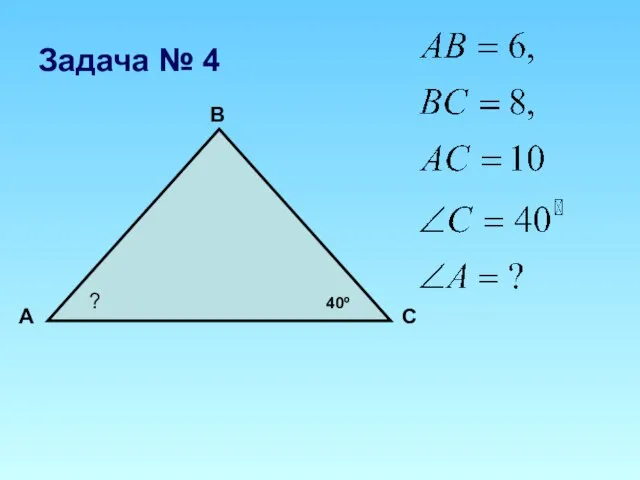
Слайд 1714) Если в треугольнике АВС
1) угол В – прямой
угол С – прямой
угол

А – прямой
угол С или угол А прямой
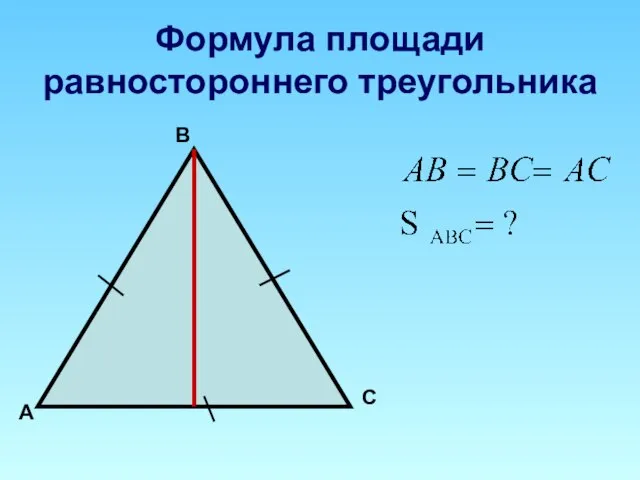
Слайд 30Формула площади равностороннего треугольника
А
В
С

















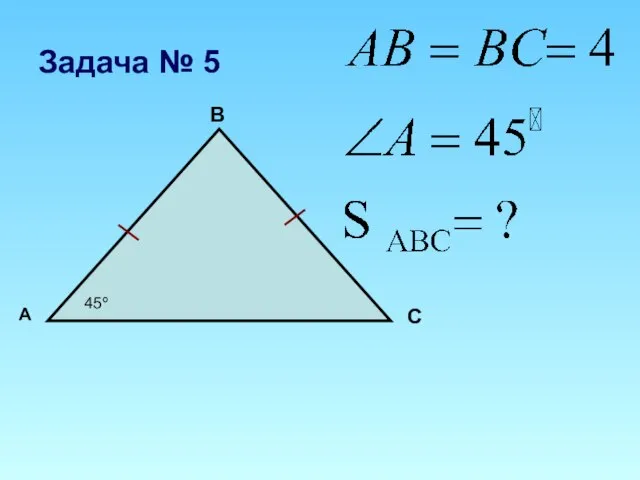
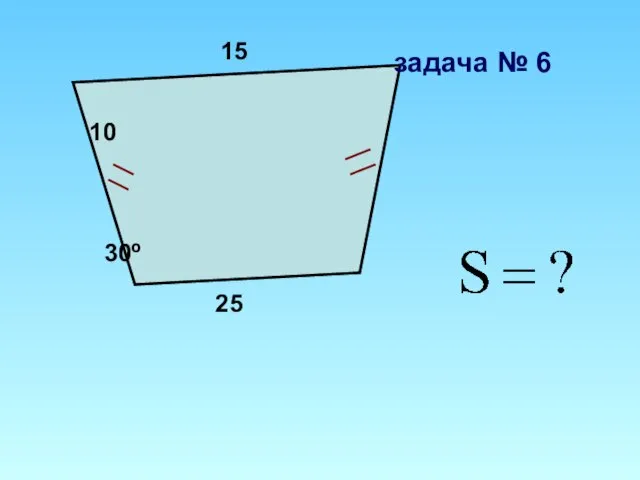
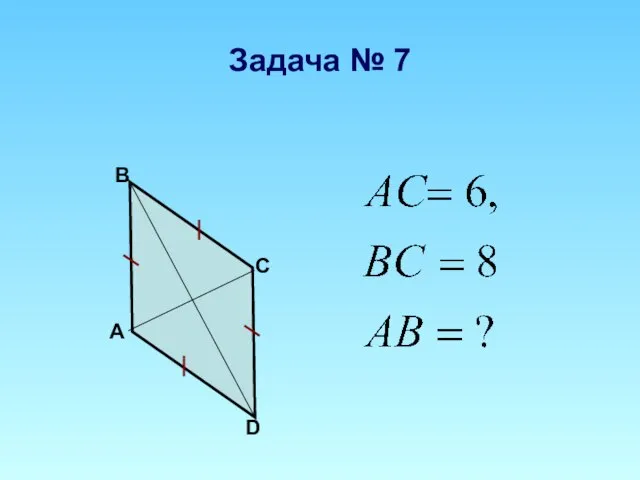
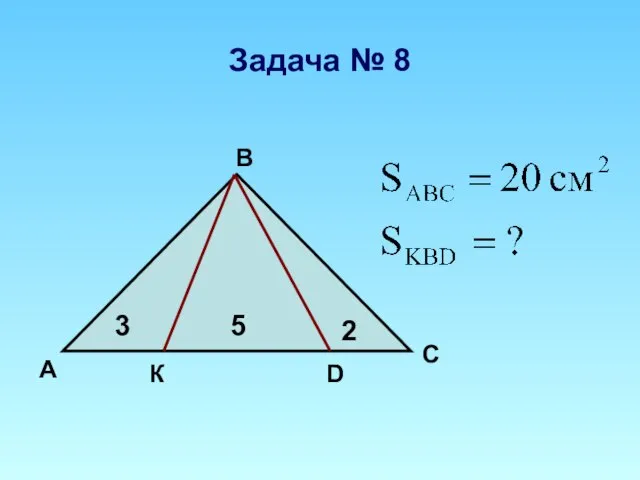
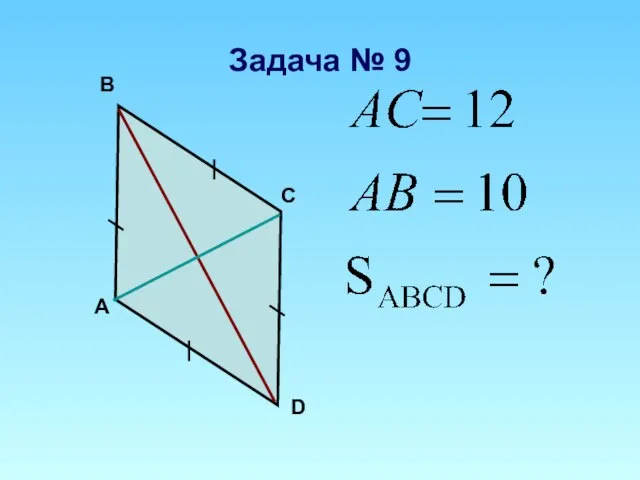
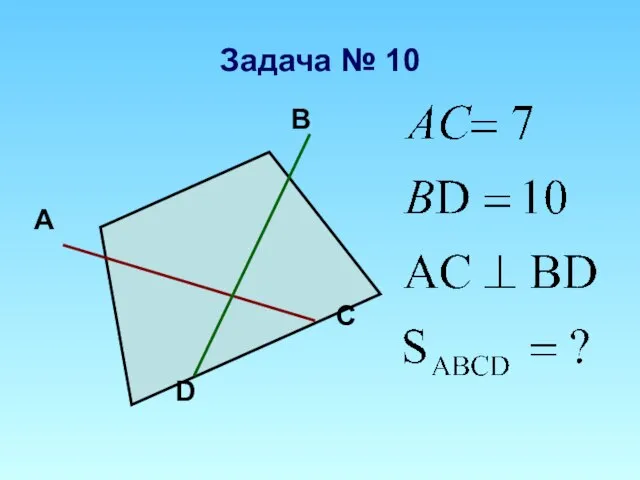
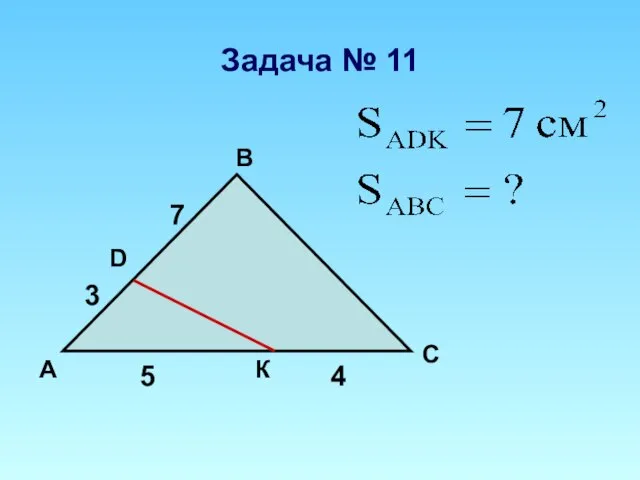
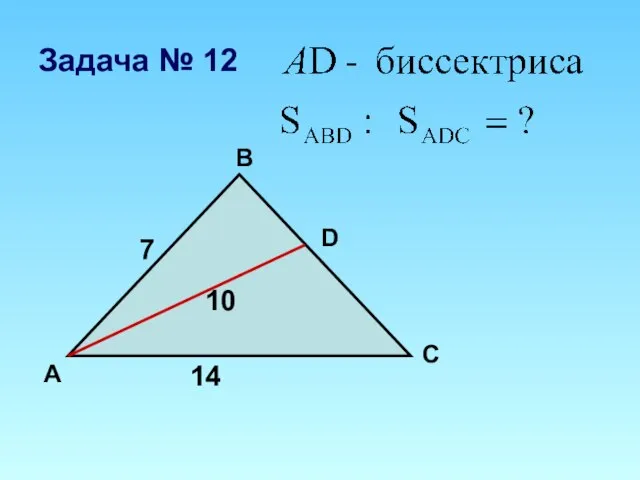

 Площадь трапеции
Площадь трапеции Египетский треугольник
Египетский треугольник Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур 23.01.13 Классная работа. Длина окружности и площадь круга.
23.01.13 Классная работа. Длина окружности и площадь круга. Урок повторения в 6 классе
Урок повторения в 6 классе Задачи на построение сечений
Задачи на построение сечений Сумма углов треугольника
Сумма углов треугольника Преобразования на плоскости
Преобразования на плоскости Геометрия
Геометрия Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Измерение объема тела
Измерение объема тела Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска Теорема Фалеса 8 класс
Теорема Фалеса 8 класс Площадь параллелограмма 8 класс
Площадь параллелограмма 8 класс Периметр – сумма длин всех сторон.
Периметр – сумма длин всех сторон. Длина окружности
Длина окружности Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Геометрия в древние и новые века
Геометрия в древние и новые века Построение диаграмм и графиков
Построение диаграмм и графиков Равнобедренный треугольник
Равнобедренный треугольник Бриллианты элементарной геометрии - презентация по Геометрии_
Бриллианты элементарной геометрии - презентация по Геометрии_ Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Шар, вписанный в пирамиду, призму, конус
Шар, вписанный в пирамиду, призму, конус Лист Мёбиуса
Лист Мёбиуса Развёртка куба
Развёртка куба Параллельность в пространстве
Параллельность в пространстве