Содержание
- 2. ? ? ? ? ? ? ? ?
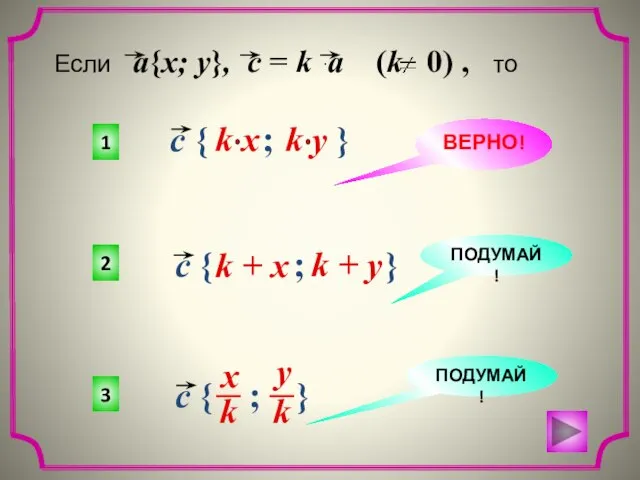
- 3. Найти координаты векторов. } }
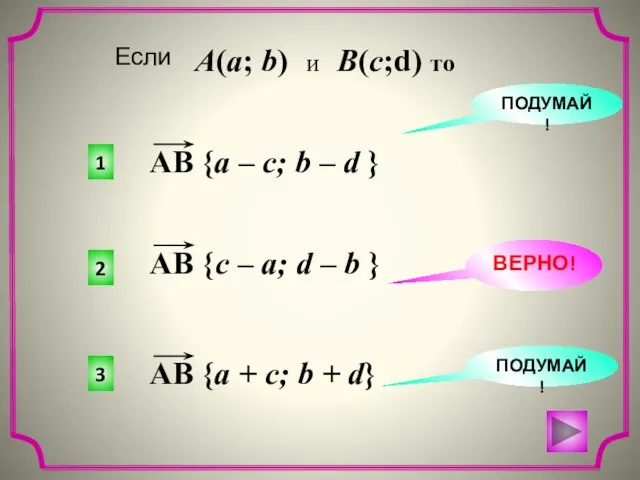
- 4. c + e Найти координаты векторов.
- 5. 3 2 1 ВЕРНО! ПОДУМАЙ! ПОДУМАЙ!
- 6. 1 2 3 ВЕРНО! ПОДУМАЙ! ПОДУМАЙ!
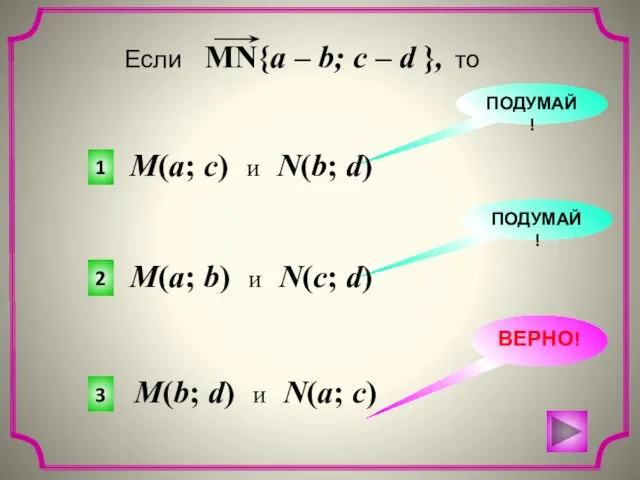
- 7. { } Найти координаты векторов. { } { } { } { } { }
- 8. 3 2 1 ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! M(a; c) и N(b; d) M(a; b) и N(c; d)
- 9. 2 1 3 ПОДУМАЙ! ВЕРНО! ПОДУМАЙ!
- 10. C (x0;y0) A(x1;y1) B(x2;y2) x y О Координаты середины отрезка
- 11. Найдите координаты cередин отрезков R(2;7); M(-2;7); C P(-5;1); D(-5;7); C R(-3;0); N(0;5); C A(0;-6); B(-4;2); C
- 12. ( ) ( ) ( ) ( ) ( ) ( ) Найти координаты середин отрезков.
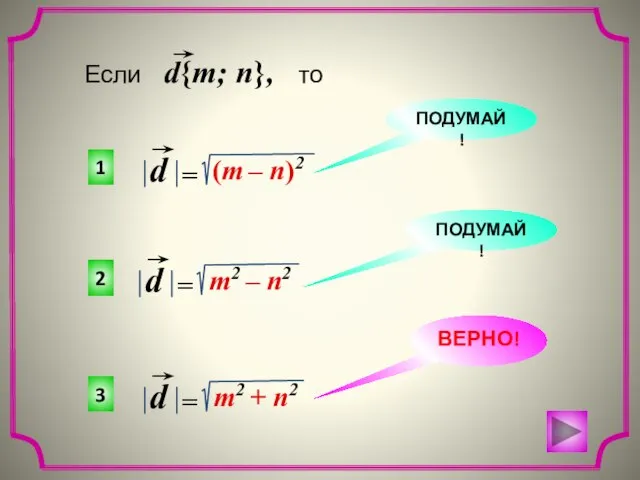
- 13. = = x y О Вычисление длины вектора по его координатам OA2=OA12 + AA12 x y
- 14. 3 2 1 ВЕРНО! ПОДУМАЙ! ПОДУМАЙ!
- 15. Расстояние между двумя точками M2(x2;y2) M1(x1;y1) d
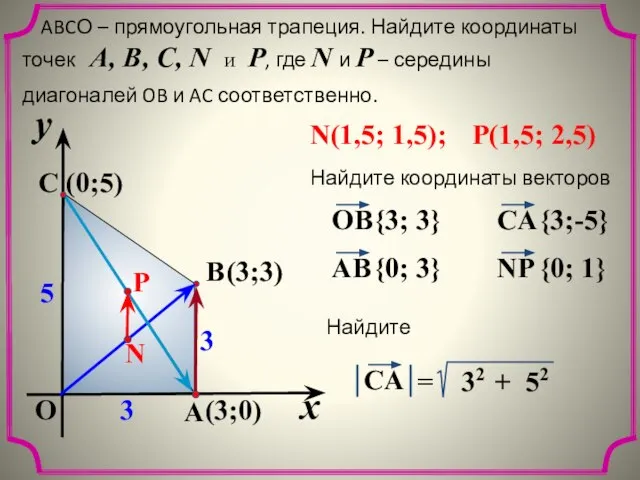
- 16. x y O A C B 5 3 3 ABCО – прямоугольная трапеция. Найдите координаты точек
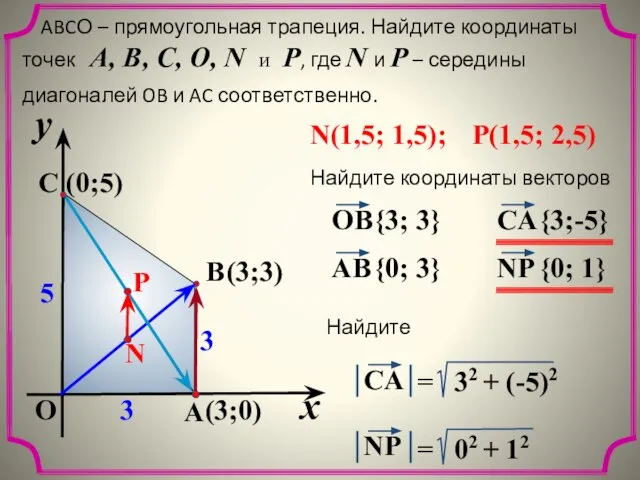
- 17. x y O A C B 5 3 3 ABCО – прямоугольная трапеция. Найдите координаты точек
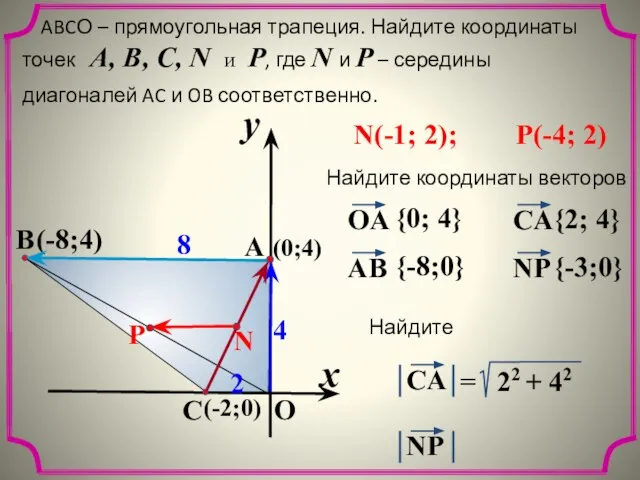
- 18. x y O A C B 8 2 4 ABCО – прямоугольная трапеция. Найдите координаты точек
- 19. x y O A C B 8 2 4 ABCО – прямоугольная трапеция. Найдите координаты точек
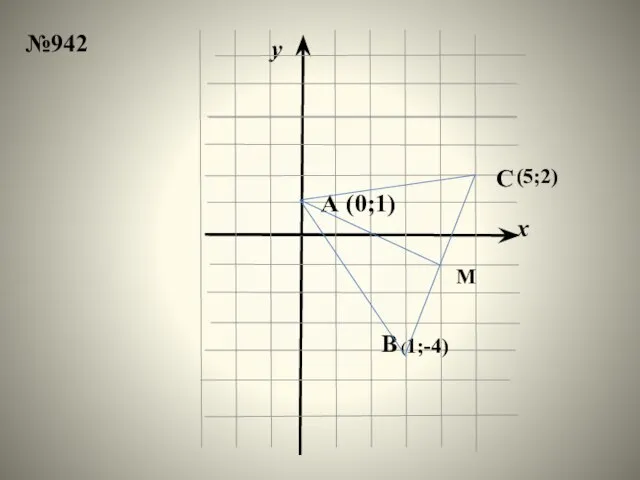
- 20. x y A (0;1) (1;-4) В С (5;2) М №942
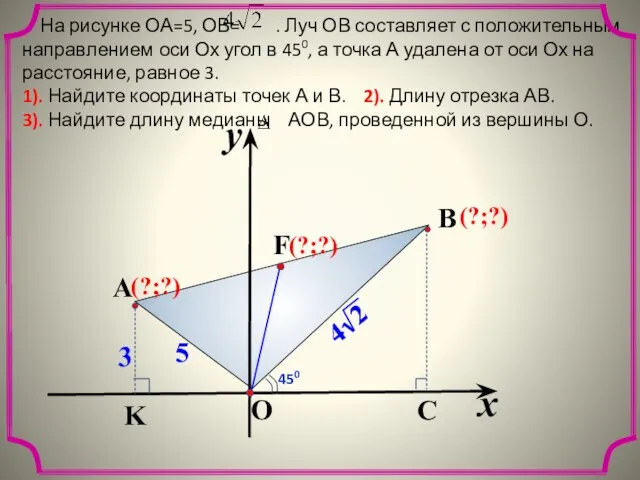
- 21. На рисунке ОА=5, ОВ= . Луч ОВ составляет с положительным направлением оси Ох угол в 450,
- 23. Скачать презентацию











 Планиметрия
Планиметрия Измерение объема тела
Измерение объема тела Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна
Підготувала вчитель математики Олексіївської ЗОШ, Нікопольсьский район Гудзь Ольга Володимирівна Правильные фигуры и тела
Правильные фигуры и тела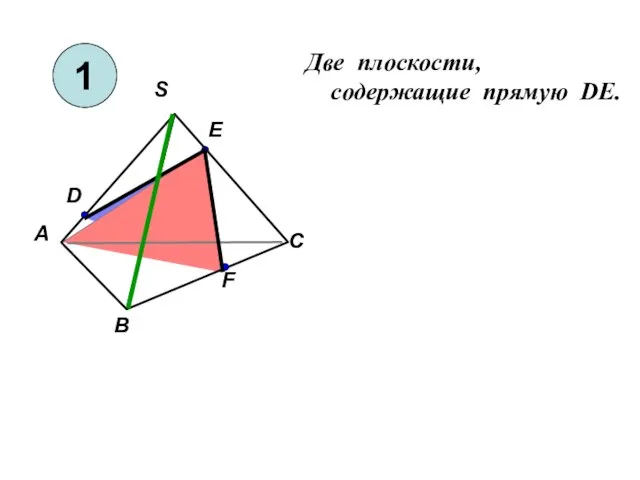 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE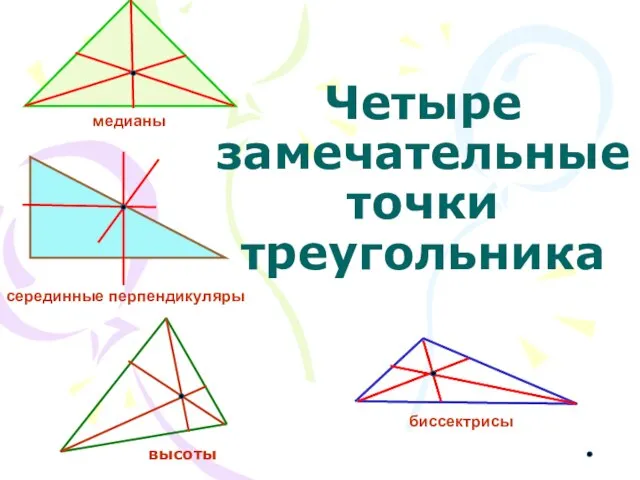 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Сумма углов треугольника
Сумма углов треугольника Магические квадраты (5 класс)
Магические квадраты (5 класс) Правильный додекаэдр
Правильный додекаэдр Объём призмы
Объём призмы Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Объём пирамиды
Объём пирамиды Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ Площадь 8 КЛАСС
Площадь 8 КЛАСС Решение треугольников
Решение треугольников Прямоугольный треугольник и его свойства - презентация по Геометрии_
Прямоугольный треугольник и его свойства - презентация по Геометрии_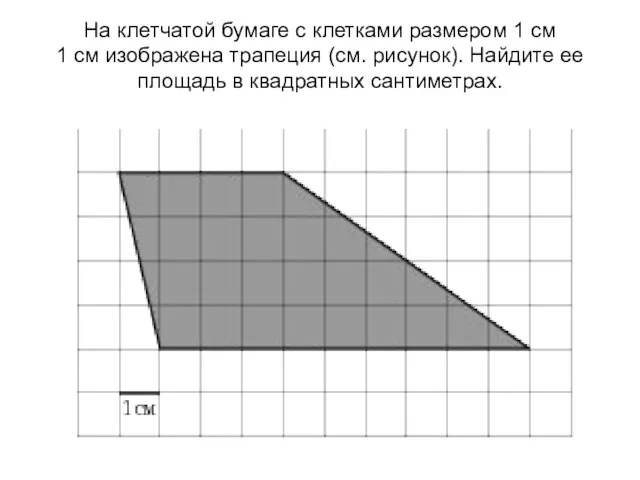 Площади фигур на клетке
Площади фигур на клетке Красота Фракталов
Красота Фракталов Площадь круга и его частей
Площадь круга и его частей Понятие цилиндра
Понятие цилиндра Правильная пирамида
Правильная пирамида Геометрия Лобачевского
Геометрия Лобачевского Угол между плоскостями
Угол между плоскостями Классификация геометрических объектов
Классификация геометрических объектов Красота, гармония, симметрия
Красота, гармония, симметрия Смежные и вертикальные углы
Смежные и вертикальные углы