Содержание
- 2. Цель урока: Выработать умение решать задачи на определение классической вероятности с использованием основных формул комбинаторики. Оборудование:
- 3. 1 этап: проверка домашнего задания Задача 1: В урне находится 3 синих, 8 красных и 9
- 4. РЕШЕНИЕ К ЗАДАЧЕ№ 1: Так как появление любого шара можно считать равновозможным, то мы имеем всего
- 5. Задача 2: Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а
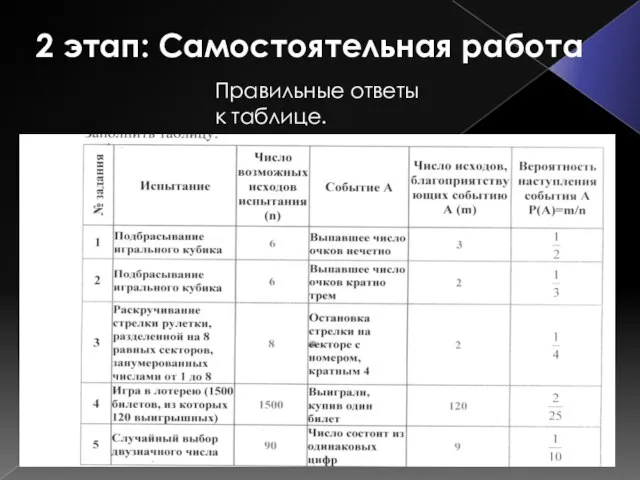
- 6. 2 этап: Самостоятельная работа Правильные ответы к таблице.
- 7. 4 этап: Практикум по решению задач. Задача 1: Таня забыла последнюю цифру номера телефона знакомой девочки
- 8. Решение: . . На последнем месте может стоять одна из 10 цифр: от 0 до 9.
- 9. Задача 2. На четырех карточках написаны буквы О, Т, К, Р. карточки перевернули и перемешали. Затем
- 10. Решение: Исходы – все возможные перестановки из четырех элементов (О, Т, К. Р);общее число исходов: n
- 11. Задача 3: На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем
- 12. Решение: Исходами опыта являются все возможные размещения четырех карточек на трех местах (порядок расположения важен). Общее
- 13. Задача 4: В ящике лежат 1 белый шар и три желтых шара. Наугад вынимают два шара.
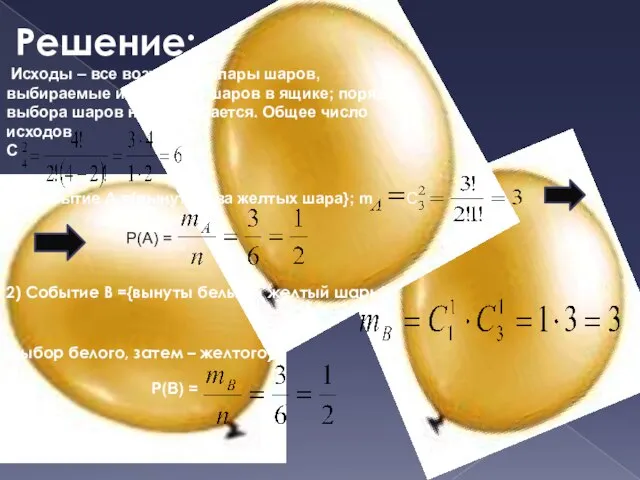
- 14. Решение: Исходы – все возможные пары шаров, выбираемые из четырех шаров в ящике; порядок выбора шаров
- 15. Задача 5: Случайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите вероятности того,
- 16. Решение: Исходы – все возможные пары букв русского алфавита без учета порядка их расположения; общее число
- 17. 2). В ={среди выбранных букв есть «ъ»}. Выбор твердого знака С выбор второй буквы из оставшихся
- 18. Домашнее задание: Задача 1: Набирая номер телефона, состоящий из 7 цифр, абонент забыл, в какой последовательности
- 19. Задача2: На каждой карточке написана одна из букв О, П, Р, С, Т. Несколько карточек наугад
- 21. Скачать презентацию
















 Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты Правильная пирамида
Правильная пирамида Шар. Сфера
Шар. Сфера Скрещивающиеся прямые
Скрещивающиеся прямые Параллельность в пространстве
Параллельность в пространстве Сумма двух векторов Геометрия -9 Урок 4
Сумма двух векторов Геометрия -9 Урок 4 Установление соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_
Установление соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_ ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Путешествие в страну Геометрия
Путешествие в страну Геометрия Признаки паралельности прямых
Признаки паралельности прямых Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А.
Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А. Параллелограмм
Параллелограмм Площади
Площади Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Вводное повторение курса геометрии
Вводное повторение курса геометрии Музей истории четырёхугольников
Музей истории четырёхугольников Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Задачи на построение сечений в параллелепипеде и тетраэдре
Задачи на построение сечений в параллелепипеде и тетраэдре Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Геометрия Лобачевского
Геометрия Лобачевского Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Прямоугольный треугольник и его свойства - презентация по Геометрии_
Прямоугольный треугольник и его свойства - презентация по Геометрии_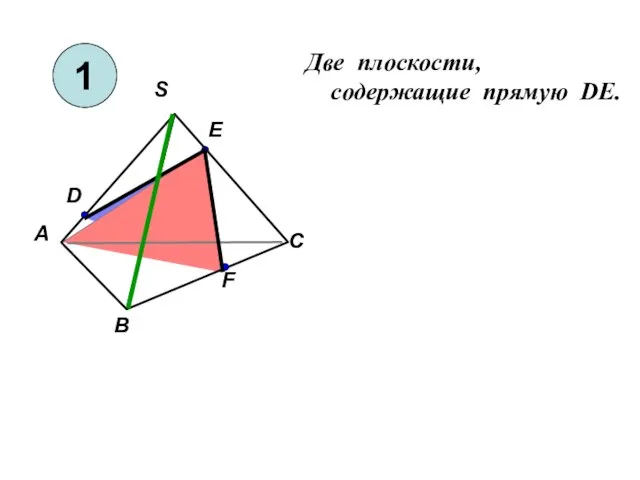 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE