можно вписать в куб, при этом шесть взаимно
перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, так что четыре
вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом
вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением
вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12
вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.
Собрать модель икосаэдра можно при помощи 20
правильных тетраэдров.




 В мире плоскостей
В мире плоскостей Цилиндр. Конус. Шар
Цилиндр. Конус. Шар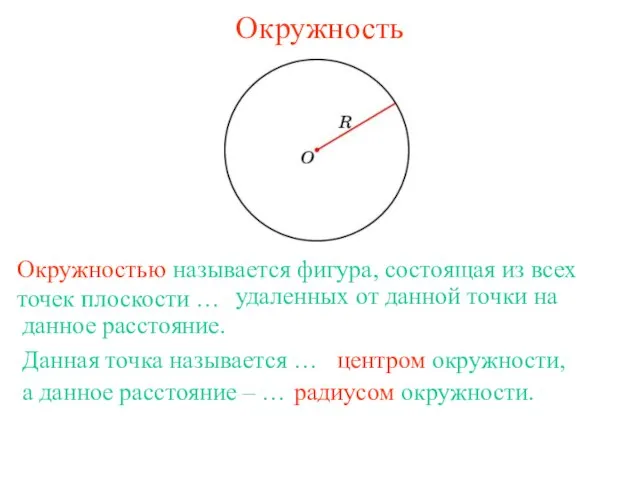 Окружность
Окружность Прямоугольник и его свойства
Прямоугольник и его свойства Угол между прямыми
Угол между прямыми Теорема, обратная теореме Пифагора - презентация по Геометрии_
Теорема, обратная теореме Пифагора - презентация по Геометрии_ Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Задачи на готовых чертежах
Задачи на готовых чертежах ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга
ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга Ромб
Ромб Преобразования на плоскости
Преобразования на плоскости Перпендикуляр и наклонная
Перпендикуляр и наклонная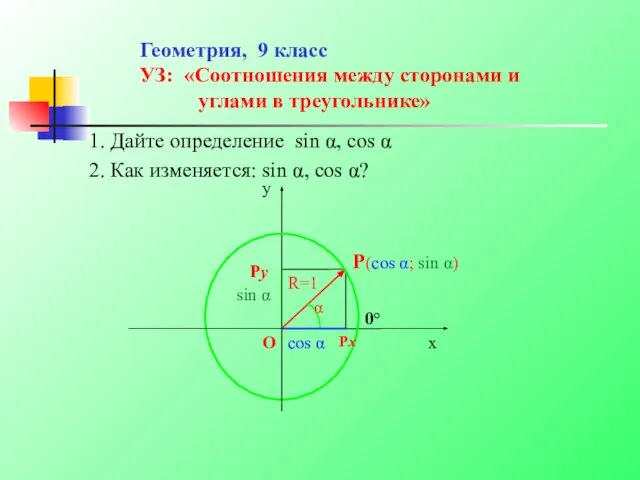 Соотношения между сторонами и углами в треугольнике
Соотношения между сторонами и углами в треугольнике Длина окружности. Площадь круга
Длина окружности. Площадь круга Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Биссектриса угла
Биссектриса угла Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д.
Учебный проект выполнен учеником 7Б класса МОАУ средней школы №58 Брыляковым Михаилом Руководитель Салангина Е.Д. Площади и объемы
Площади и объемы Решение прямоугольных треугольников
Решение прямоугольных треугольников Флексагоны
Флексагоны Учитель Лемешкина А.М.
Учитель Лемешкина А.М.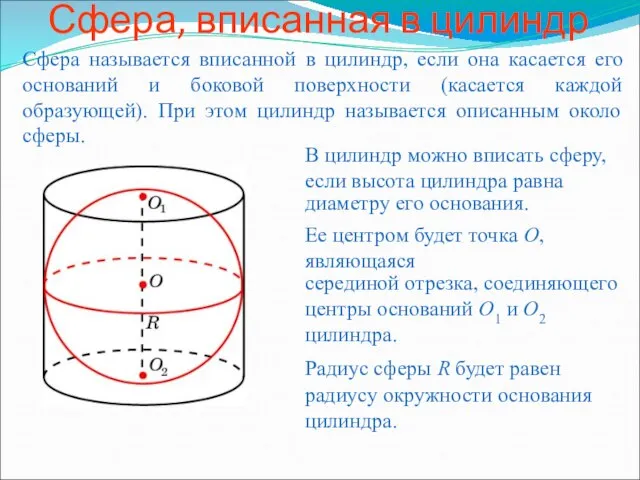 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Площадь параллелограмма 9 класс
Площадь параллелограмма 9 класс Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач