ЭНЕРГЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ

Термодинамическая система
Основным объектом изучения термодинамики является, термодинамическая система. Термодинамическая система – это совокупность материальных объектов, выделенных нами для изучения и отделенных от окружающей среды реальной или воображаемой поверхностью раздела.

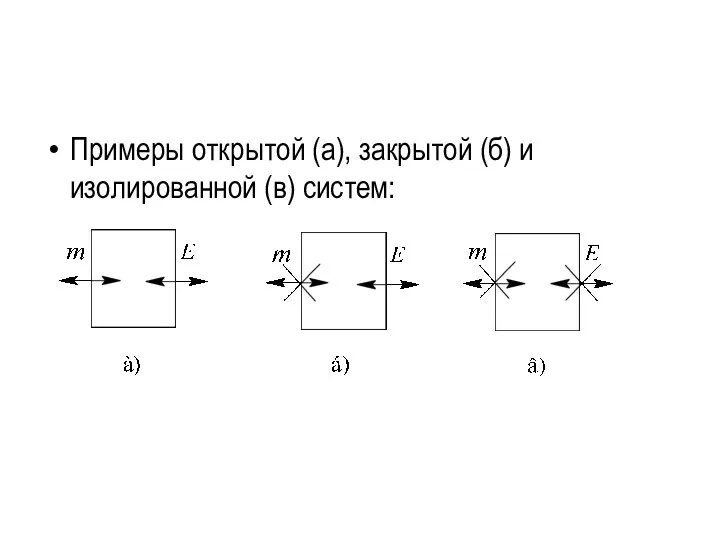
Система бывает:
открытой, если через границу, разделяющую систему и внешнюю среду, может происходить обмен веществом и энергией ( жидкость и ее пар).
закрытой, если она может обмениваться с внешней средой энергией и не может обмениваться веществом (герметически закрытый сосуд с теплопроводящими стенками).
изолированной, если система не в состоянии обмениваться с внешней средой ни веществом, ни энергией. Изолированная система – это физическая модель, не существующая в природе. Понятие изолированной системы используется при теоретических построениях.

Примеры открытой (а), закрытой (б) и изолированной (в) систем:

термодинамические параметры системы
Состояние системы определяется термодинамическими параметрами системы. Термодинамический параметр состояния – это свойство, численное значение которого не зависит от способа достижения данного состояния. В качестве параметров состояния обычно выбирают свойства, которые легко определяются экспериментально: давление (Р), температура (Т), объем (V), химическое количество вещества (n), концентрация (С) и др.

Знать состояние системы – это значит знать численные значения ее термодинамических параметров. Многие параметры зависят друг от друга и связаны между собой, например уравнением состояния идеального газа (PV = nRT). Для описания системы достаточно знать только некоторые параметры, остальные можно определить из уравнения.

Параметры могут зависеть или нет от количества вещества в системе. Экстенсивные параметры зависят от количества вещества в системе и при объединении систем складываются, т.е. обладают свойством аддитивности (масса, объем, энергия). Интенсивные параметры не зависят от количества вещества, находящегося в системе, и при объединении систем выравниваются (температура, плотность, давление, концентрация).

Термодинамический процесс
Термодинамический процесс – это переход системы из одного состояния в другое или это изменение численного значения хотя бы одного из параметров системы. Термодинамические процессы бывают самопроизвольные – протекающие без вмешательства извне (без подвода энергии), и несамопроизвольные – требующие затрат энергии извне для своего протекания

В ходе термодинамических процессов система из одного состояния переходит в другое, характеризующееся иным набором параметров. При этом могут изменяться все параметры состояния системы, либо некоторые параметры остаются без изменения.
Если процессы перехода системы происходят при постоянстве каких-то параметров системы, то они называются изобарическими.

а) изобарическими (P = const);
б) изохорическими (V = const);
в) изотермическими (Т = const);
г) изобарно-изотермическими (P = const,
Т = const).
д) адиабатическими (отсутствует теплообмен с окружающей средой,
(Q = 0).

Если термодинамические параметры состояния системы не изменяются во времени, то такая система находится в состоянии термодинамического равновесия. В зависимости от характера протекания процесса различают два типа термодинамических процессов:

1.Термодинамически обратимые процессы
Это такие процессы, которые можно провести как в прямом, так и в обратном направлении через одни и те же стадии без каких-либо изменений в окружающей среде. Эти процессы протекают бесконечно медленно через ряд стадий бесконечно близких к равновесным.

2. Необратимые термодинамические процессы
Необратимые термодинамические процессы в прямом направлении протекают не так, как в обратном. Необратимые термодинамические процессы оставляют в окружающей среде следы своего протекания. Например, двигатель внутреннего сгорания, процессы жизнедеятельности. Все реальные процессы – необратимые, они могут только в той или иной степени приближаться к обратимым.

Функции состояния
Состояние системы и происходящие в ней изменения характеризуются функциями состояния. Функцией состояния называется такая переменная характеристика системы, которая не зависит от предыстории системы и изменение которой в термодинамическом процессе зависит только от начального и конечного состояний системы и не зависит от пути перехода. К функциям состояния относятся внутренняя энергия (U), энтальпия (Н), энтропия (S), энергия Гиббса (G).

Bнутренняя энергия
Под внутренней энергией системы (U) в термодинамике понимают ее полную энергию, которая складывается из энергии поступательного, колебательного и вращательного движения, энергии притяжения и отталкивания всех частиц системы, исключая потенциальную и кинетическую энергию системы как целого.

Поскольку не определен условный нуль для внутренней энергии, то установить можно лишь ее изменение как разность значений внутренней энергии системы в конечном U2 и начальном U1 состоянии, т.е.:
ΔU = U2 – U1.

Теплота (Q) и работа (А) – две формы обмена внутренней энергией между системой и окружающей средой при условии, что переход вещества через границы системы отсутствует (закрытая система).
Количественное соотношение между изменением внутренней энергии, теплотой и работой для закрытой системы устанавливает первый закон термодинамики:
ΔU = Q – А (1)

Теплота Q – неупорядоченная форма обмена энергией между системой и средой, является результатом хаотического движения микрочастиц вещества (атомов, молекул), но не самого тела как целого. Мерой интенсивности теплового движения микрочастиц служит температура. При соприкосновении тел с разными температурами происходит выравнивание температур и изменение внутренней энергии системы. Энергия более нагретого тела в форме теплоты передается менее нагретому телу. При этом не происходит переноса вещества от одной системы к другой.

Работа А – это упорядоченная форма передачи энергии от системы среде или наоборот. В процессе совершения работы имеет место либо направленное перемещение в пространстве некоторого макроскопического объекта как целого (например, движение поршня), либо такое изменение его свойства, которое равноценно изменению пространственного положения объекта (например, уменьшение объема газа под действием внешнего давления).

Если теплота получена системой, она считается положительной величиной (Q > 0), а отданная системой во внешнюю среду – отрицательной (Q < 0). Работа, совершаемая системой над внешней средой, считается положительной (А > 0), а совершаемая над системой – отрицательной. Теплота и работа измеряются в джоулях (Дж).
Теплота, подведенная к системе, расходуется на приращение внутренней энергии системы и на работу системы над окружающей средой.

Первый закон термодинамики
Первый закон термодинамики является формой выражения закона сохранения энергии: энергия не может ни создаваться, ни исчезать, но может превращаться из одной формы в другую.

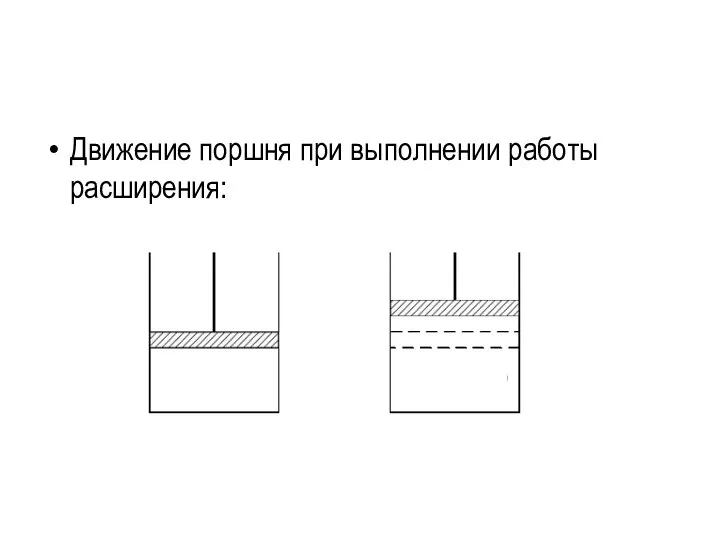
Применение первого закона термодинамики к различным процессам
Изобарический процесс. Энтальпия системы и ее изменение. Работу А можно разделить на два слагаемых: объёмную работу (работу расширения либо сжатия) P∙ΔV (P = const) и другие виды работ (полезную работу) А':
А = А' + PΔV (2),
где P – внешнее давление; ΔV – изменение объема (ΔV = V2 – V1); V2 – объем продуктов реакции; V1 – объем исходных веществ.

Движение поршня при выполнении работы расширения:

Соответственно уравнение (1) при постоянном давлении запишется в виде:
Qp = ΔU + А' + PΔV (3)
Если на систему не действуют никакие другие силы, кроме постоянного давления, т.е. при протекании химического процесса единственным видом работы является объёмная работа, то А' = 0. В этом случае уравнение (3) запишется:
Qp = ΔU + PΔV (4)

Подставив ΔU = U2 – U1, получим:
Qp = U2 – U1 + PV2 – PV1 = (U2 + РV2) – (U1 + PV1) (5)
Функция
Н = U + PV (6)
называется энтальпией системы. Энтальпия – одна из термодинамических функций, характеризующих систему, находящуюся при постоянном давлении.

Абсолютная энтальпия, как и абсолютная внутренняя энергия системы, не может быть определена. Характеристикой химического процесса является не абсолютное значение Н, а ее изменение ΔН, которое может быть измерено экспериментально. Подставив уравнение (6) в (5), получим:
Qp = Н2 – Н1 = ΔН (7)

В случае изобарического процесса
(P = const), теплота, подведенная к системе, равна изменению энтальпии системы.
Изменение энтальпии системы при протекании в ней химической реакции при условии, что система не совершает никакой другой работы, кроме работы расширения либо сжатия, называется тепловым эффектом химической реакции (энтальпией реакции) и имеет размерность кДж.

Изохорический процесс.
Если система находится в изохорических условиях (V = const, ΔV = 0), то из уравнения (4) следует:
Qv = ΔU, (8)
В этом случае тепловой эффект химической реакции равен изменению внутренней энергии системы. Из уравнения (8) следует, что энергия, сообщенная системе в форме теплоты, идет только на приращение внутренней энергии системы.

Изотермический процесс
Т = const и ΔU = 0
Для такого процесса Q = А.
Таким образом, вся сообщенная системе энергия в форме теплоты превращается в работу.

Адиабатический процесс
В адиабатическом процессе система не обменивается с окружающей средой энергией (Q = 0), работа совершается за счет уменьшения внутренней энергии системы:
А = –ΔU
Поскольку в большинстве случаев химические реакции протекают при постоянном давлении, то в дальнейшем, кроме особо оговоренных исключений, будут рассмотрены изобарические условия.

Тепловой эффект реакции обозначается ΔН. Если исходные вещества и продукты реакции находятся в стандартном состоянии, то тепловой эффект реакции называется стандартной энтальпией реакции обозначается ΔH0.
За стандартное состояние вещества принимают такое его физическое состояние, в котором чистое вещество наиболее устойчиво при давлении 1 атм (101325 Па) и определенной температуре. Температура может быть любой постоянной, но чаще всего это 298 К.

Условия стандартного состояния веществ

Если в результате реакции теплота выделяется, т.е. энтальпия системы понижается (ΔН < 0), то реакция называется экзотермической.
Реакция, протекающая с поглощением теплоты, т.е. с повышением энтальпии системы (ΔН > 0), называется эндотермической

Термохимическое уравнение
Термохимическое уравнение – это уравнение реакции со значением теплового эффекта. Тепловой эффект реакции – это количество энергии, которое выделяется или поглощается в результате реакции. Величина теплового эффекта зависит от агрегатного состояния исходных и конечных веществ, например:
(Н2) + 1/2(О2)= (Н2О); = –242 кДж/моль
(Н2) + 1/2(О2)= {Н2О}; = –286 кДж/моль

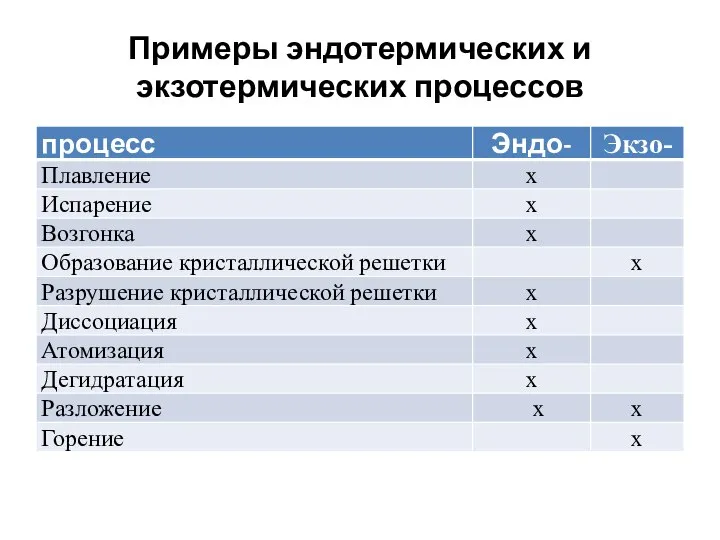
Примеры эндотермических и экзотермических процессов

Тепловой эффект реакции зависит от температуры; поэтому в индексе обычно указывается температура ΔН оT или ΔНо298 (Р = 1 атм).
Учет зависимости изменения энтальпии реакции от температуры актуален для точных термодинамических вычислений. В ряде случаев зависимостью изменения энтальпии химической реакции от температуры можно пренебречь. Для большинства реакций изменение теплового эффекта в пределах температур, имеющих практическое значение, относительно невелико.

Например, тепловой эффект реакции окисления графита: (С + СО2 = 2СО) при увеличении температуры с 500 до 1500 K изменяется на 5%, а реакции окисления азота (N2 + О2 = 2NO) при повышении температуры с 298 до 4000 K – лишь на 2,2%. Поэтому в дальнейшем будут использоваться значения ΔНо298 вместо ΔНоТ :
ΔН оТ ≈ ΔНо298

Влияние давления на тепловой эффект можно не учитывать, так как в пределах давлений, используемых в практике, эффект давления для большинства реакций относительно невелик. Например, при увеличении давления с 105 до 5 · 107 Па тепловой эффект реакции синтеза аммиака:
N2 + 3Н2 = 2NН3
изменяется на 5%. Поэтому в дальнейшем в расчетах влияние давления на энтальпию реакции не будет учитываться, а будут использоваться стандартные значения энтальпий реакций (ΔН0).

Стандартная энтальпия (теплота) образования. Тепловой эффект образования 1 моля вещества из простых веществ, устойчивых при 298 K и давлении 101,325 кПа, называют стандартной энтальпией (теплотой) образования. Стандартную энтальпию образования вещества обозначают ΔН0f,298. Знак (0) означает, что вещество находится в стандартном состоянии. Буква f от английского formation (образование) означает, что это энтальпия образования данного вещества из простых веществ, а не из каких-нибудь других. Индекс 298 означает, что энтальпия образования определена или рассчитана при 298 K.

Стандартную энтальпию образования простых веществ, устойчивых при 298 К и давлении 101,325 кПа, принимают равной нулю.
Нулевое значение энтальпии образования имеет фаза или модификация вещества, наиболее устойчивая при 298 К и давлении 101,325 кПа: газообразный кислород, жидкий бром, белое олово, ромбическая сера. Например:
ΔН0f,298 (О2) = 0 кДж/моль,
но ΔН 0f,298 (О3) = 142,3 кДж/моль.

Величины стандартных энтальпий образования ΔН0f,298 определены с той или иной степенью точности для большого числа веществ и приведены в справочниках. Если стандартная энтальпия образования отрицательна, соединение более устойчиво, чем простые вещества, из которых оно образовалось. Если она положительна, соединение менее устойчиво, чем простые вещества, образовавшие его.
Эндотермические соединения (ΔН0f,298 > 0) неустойчивы и склонны к распаду. Получают их, как правило, косвенным путем.

Если ΔН0f,298 < 0, то в ряду однотипных соединений, чем меньше ΔН0f,298 , тем больше его термическая устойчивость относительно разложения на простые вещества. Так в приведенном ряду термическая устойчивость соединений уменьшается:

Стандартная молярная энтальпия сгорания вещества (ΔН0сгор., 298 ) соответствует изменению энтальпии при сгорании в кислороде 1 моля вещества при температуре 298 K и давлении 1 атм с образованием углекислого газа, жидкой воды, N2, SO2, стандартные теплоты сгорания которых приняты равными нулю, например:
(C3H8) + 5(O2) → 3(CO2) + 4{H2O},
ΔН0сгор., 298 = –2220 кДж/моль
Стандартные молярные энтальпии сгорания многих соединений приведены в справочной литературе.

Стандартная энтальпия растворения – это изменение энтальпии при растворении 1 моля вещества с образованием бесконечно разбавленного раствора. При этом предполагается, что энтальпия не зависит от концентрации раствора. Складывается из теплоты разрушения кристаллической решетки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием гидратов (сольватов).

Разрушение кристаллической решетки – эндотермический процесс (ΔHореш > 0), а гидратация ионов – экзотермический
(ΔHогидр < 0). В зависимости от соотношения значений ΔHореш и ΔHогидр энтальпия растворения может иметь как положительное (например, растворение нитрата аммония), так и отрицательное значение (растворение гидроксида калия).

При расчете изменения энтальпий химических реакций, протекающих в растворах, используют значения стандартных энтальпий образования ионов для диссоциирующих в воде соединений и стандартные энтальпии образования соединений для тех веществ, которые не подвергаются диссоциации. За нуль принята энтальпия образования 1 моля иона водорода в 1 дм3 водного раствора в стандартных условиях (давление 1 атм (101,325 kПа) и температура 298 К). Стандартные энтальпии образования других ионов определены относительно стандартной энтальпии образования иона водорода в растворе и приведены в справочной литературе.

Стандартная молярная энтальпия нейтрализации – изменение энтальпии при образовании 1 моля воды в результате нейтрализации каких-либо кислоты и щелочи при температуре 298 K и давлении 1 атм.
В случае нейтрализации сильной щелочи сильной кислотой стандартная молярная энтальпия нейтрализации равна
–55,65 kДж/моль. Это объясняется тем, что любые реакции нейтрализации сильных кислот и щелочей можно описать одним и тем же ионным уравнением:
{H+} + {ОH–} → {H2O}, ΔН0298 = –55,65 кДж/моль

Калориметрия
Для измерения количества энергии, высвобождаемой или поглощаемой в результате химической реакции или физического превращения используют специальные приборы – калориметры.

ТЕРМОХИМИЧЕСКИЕ РАСЧЕТЫ
Раздел химии, изучающий тепловые эффекты химических реакций и фазовых превращений, называется термохимией.
Термохимические уравнения иногда имеют дробные коэффициенты:
2[Al] + (O2) = [Al2O3]; ΔНо = –1675,8кДж

В термохимических уравнениях указываются агрегатные состояния и модификации исходных веществ и продуктов реакции:
(СО2) + [Cграфит] = 2(СО); ΔНо = 172,47 кДж

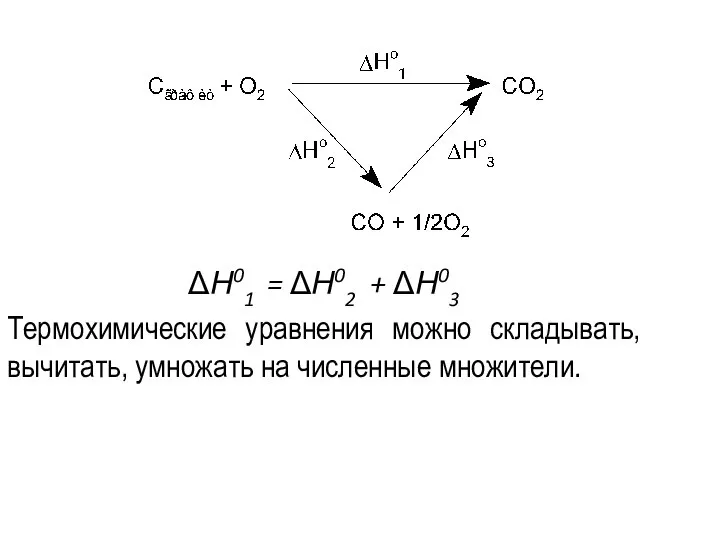
Закон Гесса
Термохимические расчеты основаны на законе Гесса: тепловой эффект реакции при постоянных температуре и давлении зависит только от природы и состояния исходных и конечных веществ и не зависит от числа и характера промежуточных стадий.

ΔН01 = ΔН02 + ΔН03
Термохимические уравнения можно складывать, вычитать, умножать на численные множители.

Пример 1. Вычислить теплоту образования СО, если известны тепловые эффекты реакций:
Сграфит + О2 → СО2, ΔН01 = –393,5 кДж/моль,
СО + О2 → СО2, ΔН03 = –283,0 кДж
Сграфит + 1/2О2 → СО, ΔН02 = – ?
Последнее уравнение получается, если из первого вычесть второе. Следовательно,
ΔН02 = ΔН01 – ΔН03 = –110,5 кДж/моль

1-е следствие из закона Гесса
Применяют в термохимических расчетах : тепловой эффект реакции ( ) равен сумме стандартных теплот образования (ΔН0f,298 ) продуктов реакции за вычетом суммы стандартных теплот образования исходных веществ с учетом стехиометрических коэффициентов:
= –
–

При вычислении тепловых эффектов различных процессов необходимо:
1) записать соответствующий процесс, указав агрегатные состояния веществ, участвующих в реакции;
2) расставить стехиометрические коэффициенты;
3) выписать из справочника значения стандартных энтальпий образования ΔН0f,298 всех участвующих в реакции веществ в соответствующих агрегатных состояниях;
4) используя 1-ое следствие из закона Гесса, рассчитать тепловой эффект процесса (ΔН0298 ). Стехиометрические коэффициенты необходимо учитывать, так как энтальпия является экстенсивной величиной.

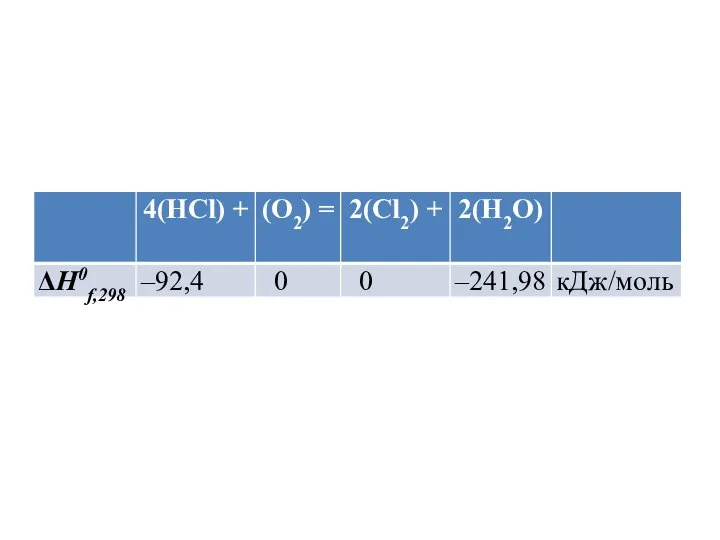
Пример 2. Рассчитать тепловой эффект (изменение энтальпии) реакции
4(HCl) + (O2) = 2(Cl2) + 2(H2O)
в стандартных условиях.
Решение. Записываем уравнение реакции со стехиометрическими коэффициентами, обозначив агрегатные состояния веществ. Под формулой каждого из веществ выписываем из справочника значения стандартных энтальпий образования:

4(HCl) + (O2) = 2(Cl2) + 2(H2O)
Используя следствие из закона Гесса, рассчитываем тепловой эффект реакции:
ΔН 0298 = 2ΔН0f,298 (H2O) + 2ΔН0f,298 (Cl2) – 4ΔН 0f,298 (HCl) – ΔН0f,298 (O2) =
= 2 ⋅ (–241,98) + 2 ⋅ 0 – 4(–92,4) – 0=
= –114,36 кДж

Пример 3. Рассчитать тепловой эффект процесса испарения воды.
Решение. {H2O} = (H2O)
ΔH0f,298 –285,84 –241,98 кДж/моль;
ΔH0298 = (–241,98) – (–285,84) = 43,86 кДж.
Процесс является эндотермическим

Пример 4. Рассчитать тепловой эффект реакции нейтрализации 1 моля соляной кислоты 1 молем гидроксида калия в стандартных условиях.
Решение. Расчет изменения энтальпии процессов, протекающих в растворах, проводят, используя сокращенные ионно-молекулярные уравнения соответствующих процессов:
{HCl} + {KOH} = {KCl} + {H2O}
{H+} + {ОH–} = {H2O},
ΔH0f,298 0 –230,19 –285,84 кДж/моль;
ΔН0298 = –285,84 + 230,19 = –55,65 кДж

Пример 5. Рассчитать тепловой эффект растворения 1 моля нитрата калия.
Решение. При растворении нитрат калия диссоциирует на ионы:
ΔН0298 растворения = –251,2 – 207,5 + 493,2 = 34,5 кДж/моль
Растворение нитрата калия – эндотермический процесс

Рассчитать тепловой эффект ионизации 1 моль атомов хлора.
Запишем процесс ионизации хлора: Cl г + e– = Cl̶–г
ΔH , кДж/моль 121,31 –233,62
ΔН = –233,62 – 121,31 = –354,93 кДж/моль

Расчет энергиии связи
Под энергией (энтальпией) связи А–В в молекуле АВ понимают энергию (энтальпию) разрыва 1 моль связей
А–В, при этом атомы разводятся на бесконечно большое расстояние. Разорвать связи на атомы возможно только в газовой фазе.

Под средней энергией связи А–В в молекуле АВn, понимают 1/n часть энтальпии разрыва всех связей в 1 моль молекул АВn до состояния атомов. Атомы разводятся на бесконечно большое расстояние.
Например:
NH3 г = N г + 3H г; ΔН = 3ΔН ср.связи N-H.

2-е следствие из закона Гесса
применимо к процессам с участием органических веществ: тепловой эффект реакции равен сумме стандартных теплот сгорания исходных веществ с учетом стехиометрических коэффициентов за вычетом суммы стандартных теплот сгорания продуктов реакции с учетом стехиометрических коэффициентов:
ΔН = –
ΔН
=
–
.