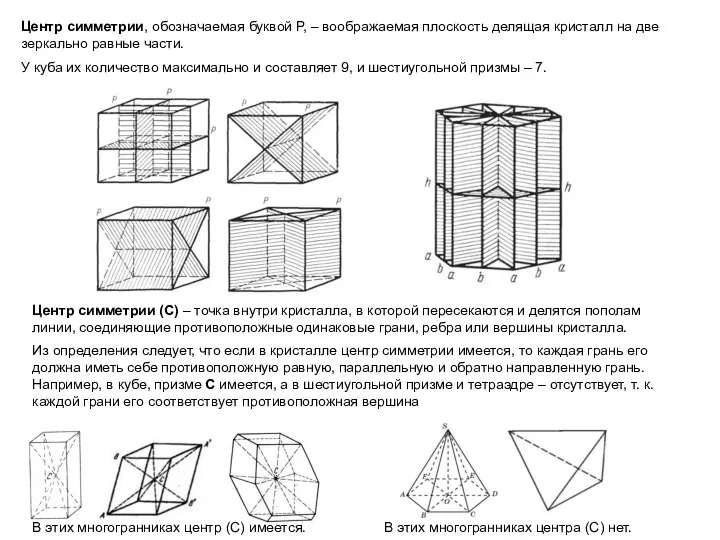
зеркально равные части.
У куба их количество максимально и составляет 9, и шестиугольной призмы – 7.
Центр симметрии (С) – точка внутри кристалла, в которой пересекаются и делятся пополам линии, соединяющие противоположные одинаковые грани, ребра или вершины кристалла.
Из определения следует, что если в кристалле центр симметрии имеется, то каждая грань его должна иметь себе противоположную равную, параллельную и обратно направленную грань. Например, в кубе, призме С имеется, а в шестиугольной призме и тетраэдре – отсутствует, т. к. каждой грани его соответствует противоположная вершина
В этих многогранниках центр (С) имеется.
В этих многогранниках центра (С) нет.

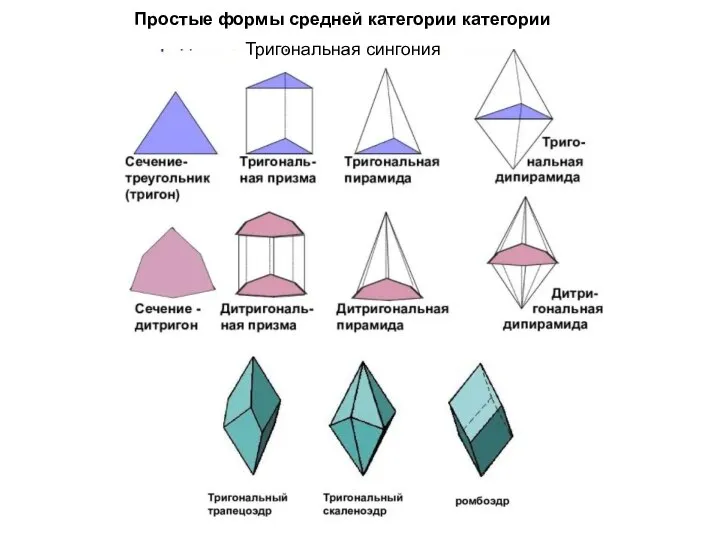
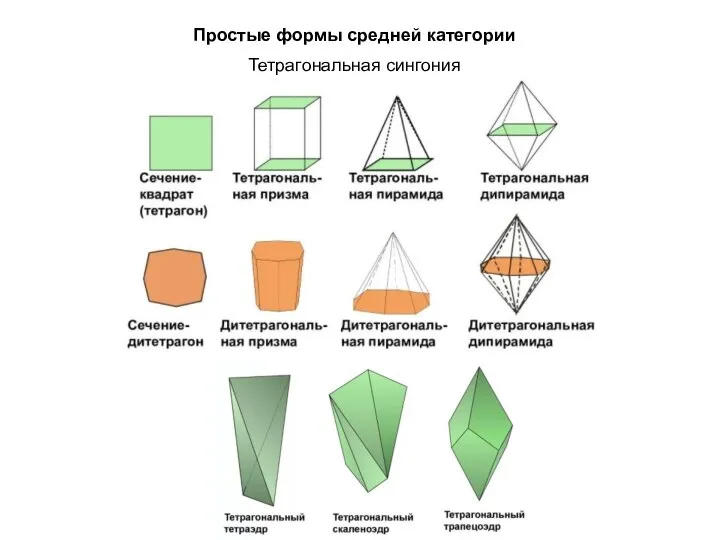
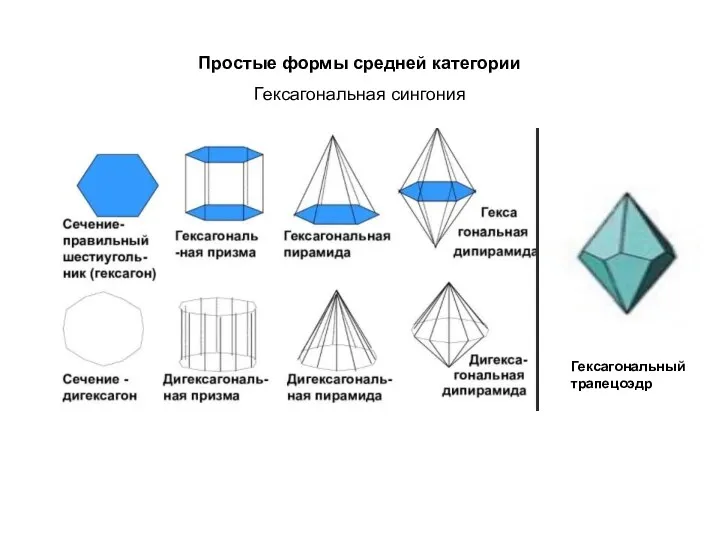
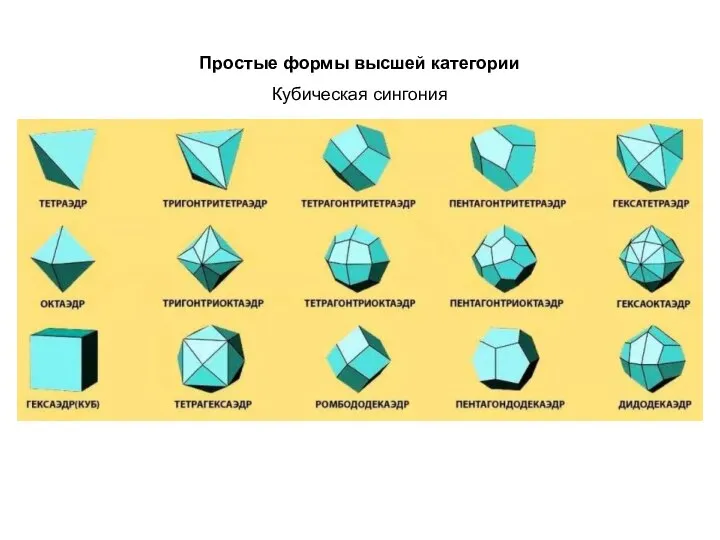
 Оксиды. Классификация, химические и физические свойства
Оксиды. Классификация, химические и физические свойства Реакции ионного обмена
Реакции ионного обмена Презентация на тему Виды кристаллических решеток
Презентация на тему Виды кристаллических решеток  Изучение ТЭД и ОВР в школьном курсе химии
Изучение ТЭД и ОВР в школьном курсе химии Соли: получение
Соли: получение Устный журнал из истории развития химии
Устный журнал из истории развития химии Предельные углеводороды. Тест 19
Предельные углеводороды. Тест 19 Виды аккумулирования энергии
Виды аккумулирования энергии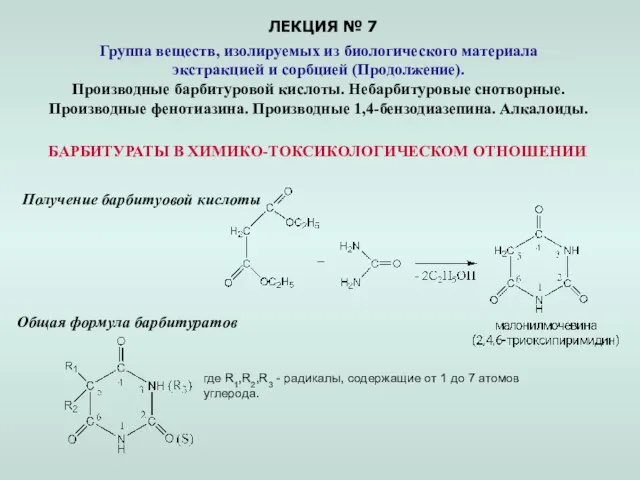 Презентация по Химии "Группа веществ, изолируемых из биологического материала экстракцией и сорбцией"
Презентация по Химии "Группа веществ, изолируемых из биологического материала экстракцией и сорбцией"  Важнейшие классы неорганических соединений. Соли
Важнейшие классы неорганических соединений. Соли Презентация на тему Химия и пища
Презентация на тему Химия и пища  Способы получения металлов
Способы получения металлов Химические свойства кислот с точки зрения ТЭД
Химические свойства кислот с точки зрения ТЭД Углеводы. Глюкоза
Углеводы. Глюкоза Классификация минералов + самородные элементы. Занятие 5
Классификация минералов + самородные элементы. Занятие 5 АРЕНЫ
АРЕНЫ 01_Osnovnye_ponyatia_i_zakony_khimii
01_Osnovnye_ponyatia_i_zakony_khimii Презентация по Химии "Углекислый газ"
Презентация по Химии "Углекислый газ"  Основные химические понятия и законы химии. (Часть 2)
Основные химические понятия и законы химии. (Часть 2) НХ 3 Термохимия
НХ 3 Термохимия Презентация на тему Электролиз: что полезно знать
Презентация на тему Электролиз: что полезно знать  Гидролиз солей – частный случай РИО
Гидролиз солей – частный случай РИО Классификация методов аналитической химии
Классификация методов аналитической химии Исследование кокаина методом ГХ-МС
Исследование кокаина методом ГХ-МС Магний и кальций
Магний и кальций Фтор. Биологическое значение, соединения и применение
Фтор. Биологическое значение, соединения и применение Классификация неорганических веществ
Классификация неорганических веществ Презентация на тему Подгруппа кислорода
Презентация на тему Подгруппа кислорода