Перициклические реакции

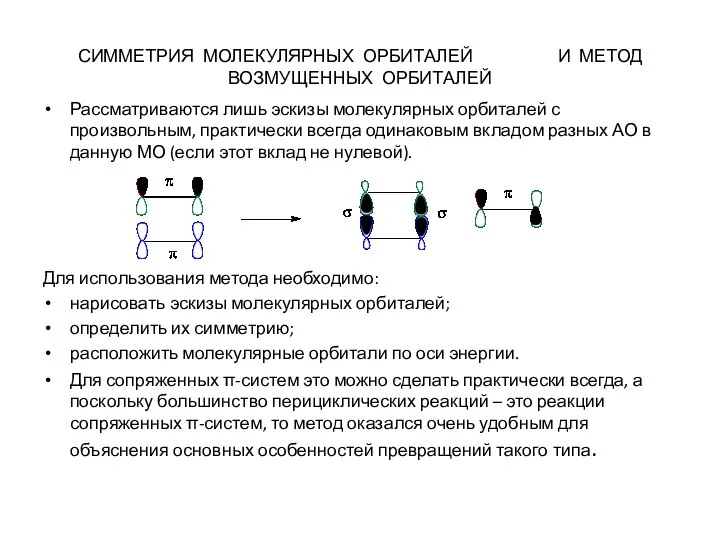
СИММЕТРИЯ МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ И МЕТОД ВОЗМУЩЕННЫХ ОРБИТАЛЕЙ
Рассматриваются лишь эскизы молекулярных орбиталей с произвольным, практически всегда одинаковым вкладом разных АО в данную МО (если этот вклад не нулевой).
Для использования метода необходимо:
нарисовать эскизы молекулярных орбиталей;
определить их симметрию;
расположить молекулярные орбитали по оси энергии.
Для сопряженных π-систем это можно сделать практически всегда, а поскольку большинство перициклических реакций – это реакции сопряженных π-систем, то метод оказался очень удобным для объяснения основных особенностей превращений такого типа.

Теория возмущений молекулярных орбиталей
Основной вопрос, на который отвечает теория ВМО:
как будет изменяться энергия системы (повысится или понизится) в том случае, если две молекулы начнут сближаться на расстояние меньше, чем ван-дер-ваальсовские радиусы. Это изменение энергии является определяющим фактором для осуществления превращения:
если энергия системы повышается, молекулы расходятся, а если понижается, то происходит реакция.
Следует отметить, что в теории ВМО не рассматривается весь путь от реагентов через переходное состояние к продуктам. Смысл термина «реакционная способность» в этой теории заключается в том, что способность молекул вступать в реакцию определяется их собственными структурными свойствами.
Реакция рассматривается только в самый начальный момент ее развития. В этот момент реагент испытывает малые возмущения со стороны другого реагента. Малым возмущениям соответствуют малые изменения энергии, которые представляются как расщепление первичных уровней энергии.

Предполагается, что при перекрывании орбиталей реагирующих молекул две (или большее число) первоначально невозмущенные (базисные) орбитали взаимодействуют таким образом, что это приводит к образованию двух новых возмущенных орбиталей. Одна из двух новых орбиталей имеет более низкую, а другая – более высокую энергию, чем базисные орбитали. Следует отметить, что эти две возмущенные орбитали не являются орбиталями продукта реакции, а соответствуют слабому комплексу между двумя молекулами. Комплекс образуется на ранней стадии реакции и его можно рассматривать как пару сближенных друг с другом молекул. Такой комплекс называют «супермолекулой». В «супермолекуле» каждый из составляющих ее партнеров практически сохраняет свойства изолированной молекулы.
Рассмотрим, как происходит формирование новых орбиталей в следующих простых реакциях:
а) объединение двух протонов в «молекулу» Н22+ (реакция чисто гипотетическая),

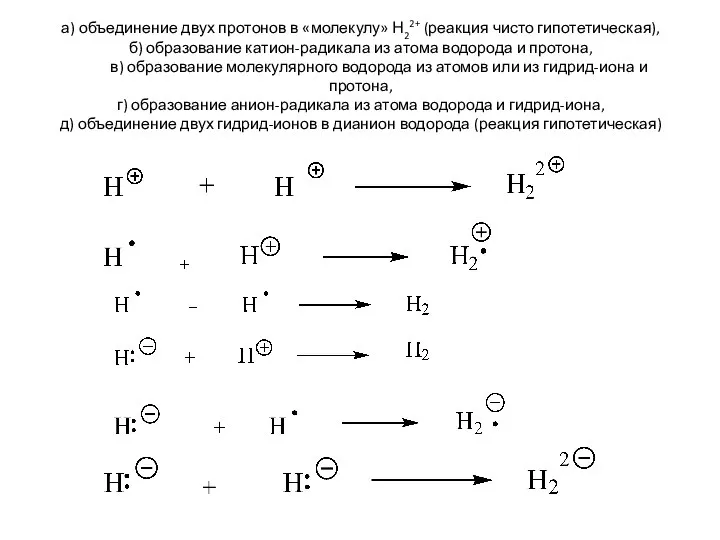
а) объединение двух протонов в «молекулу» Н22+ (реакция чисто гипотетическая),
б) образование катион-радикала из атома водорода и протона,
в) образование молекулярного водорода из атомов или из гидрид-иона и протона,
г) образование анион-радикала из атома водорода и гидрид-иона,
д) объединение двух гидрид-ионов в дианион водорода (реакция гипотетическая)

Во всех этих случаях сближающиеся частицы имеют по одной 1s-атомной орбитали (1s-АО). Согласно теории возмущения, при достаточном сближении частиц происходит перекрывание 1s АО. Из этих двух 1s АО образуются две новые «возмущенные» орбитали, одна из которых лежит ниже базисных атомных 1s-АО, а вторая − выше базисных атомных 1s-орбиталей.
Нижняя возмущенная МО образуется путем перекрывания в фазе (положительная интерференция), и амплитуда волновой функции в пространстве между ядрами возрастает (рис. 2). Эта σ-МО называется связывающей.
Верхняя возмущенная МО образуется путем вычитания волновых функций, т. е. путем их перекрывания в противофазе (отрицательная интерференция), и амплитуда волновой функции на середине межъядерной линии равна нулю.
Эта σ-МО называется антисвязывающей или разрыхляющей (обозначается σ*).

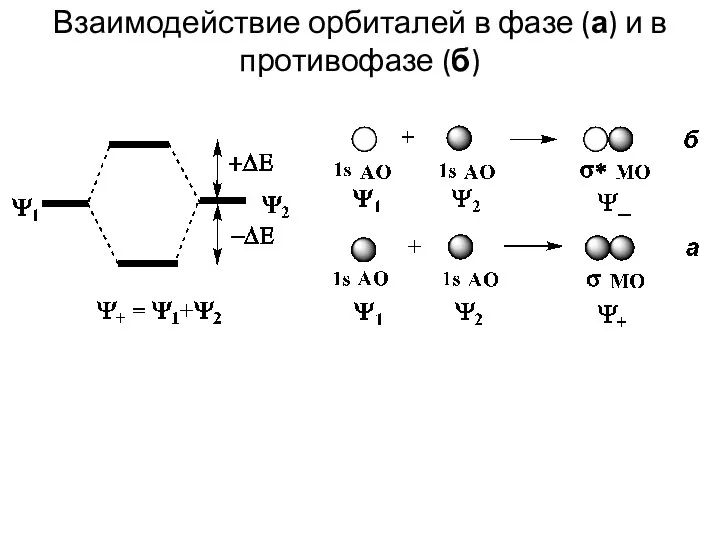
Взаимодействие орбиталей в фазе (а) и в противофазе (б)

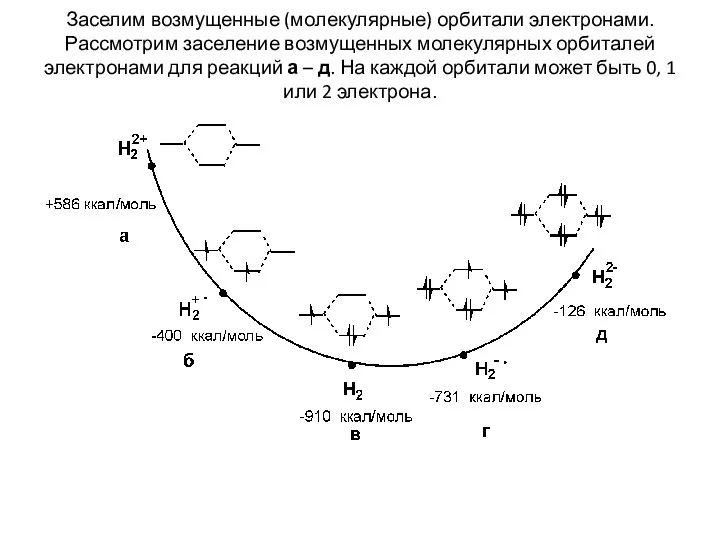
Заселим возмущенные (молекулярные) орбитали электронами. Рассмотрим заселение возмущенных молекулярных орбиталей электронами для реакций а – д. На каждой орбитали может быть 0, 1 или 2 электрона.

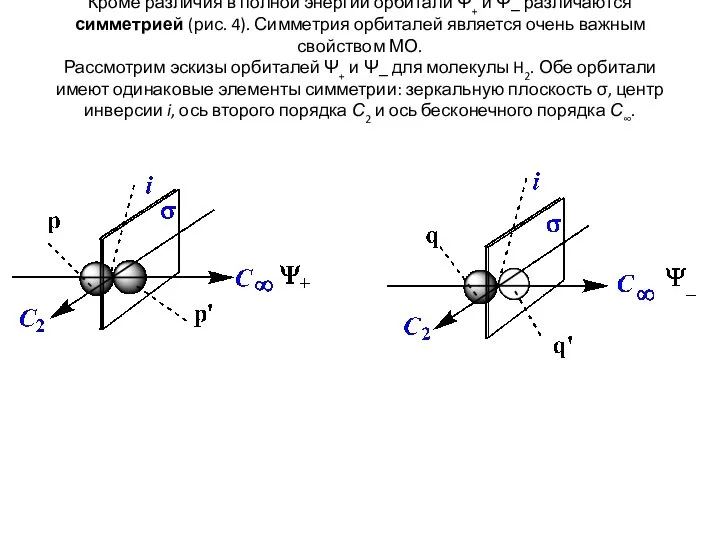
Кроме различия в полной энергии орбитали Ψ+ и Ψ_ различаются симметрией (рис. 4). Симметрия орбиталей является очень важным свойством МО.
Рассмотрим эскизы орбиталей Ψ+ и Ψ_ для молекулы H2. Обе орбитали имеют одинаковые элементы симметрии: зеркальную плоскость σ, центр инверсии i, ось второго порядка С2 и ось бесконечного порядка С∞.

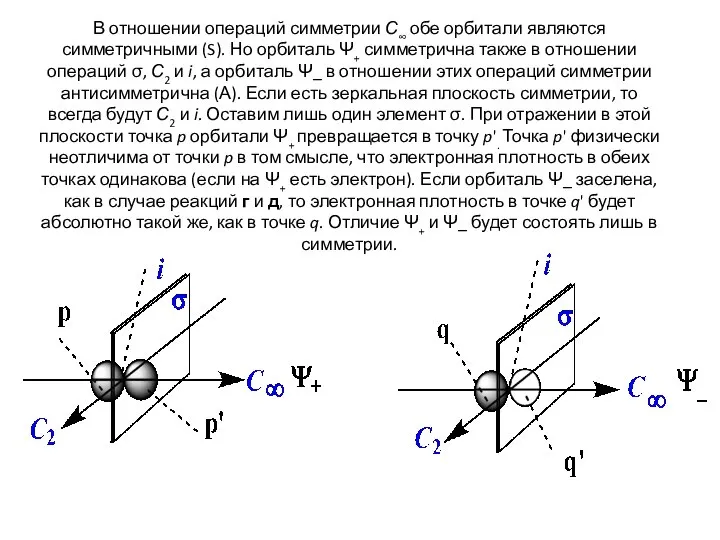
В отношении операций симметрии С∞ обе орбитали являются симметричными (S). Но орбиталь Ψ+ симметрична также в отношении операций σ, С2 и i, а орбиталь Ψ_ в отношении этих операций симметрии антисимметрична (А). Если есть зеркальная плоскость симметрии, то всегда будут С2 и i. Оставим лишь один элемент σ. При отражении в этой плоскости точка p орбитали Ψ+ превращается в точку p'. Точка p' физически неотличима от точки p в том смысле, что электронная плотность в обеих точках одинакова (если на Ψ+ есть электрон). Если орбиталь Ψ_ заселена, как в случае реакций г и д, то электронная плотность в точке q' будет абсолютно такой же, как в точке q. Отличие Ψ+ и Ψ_ будет состоять лишь в симметрии.

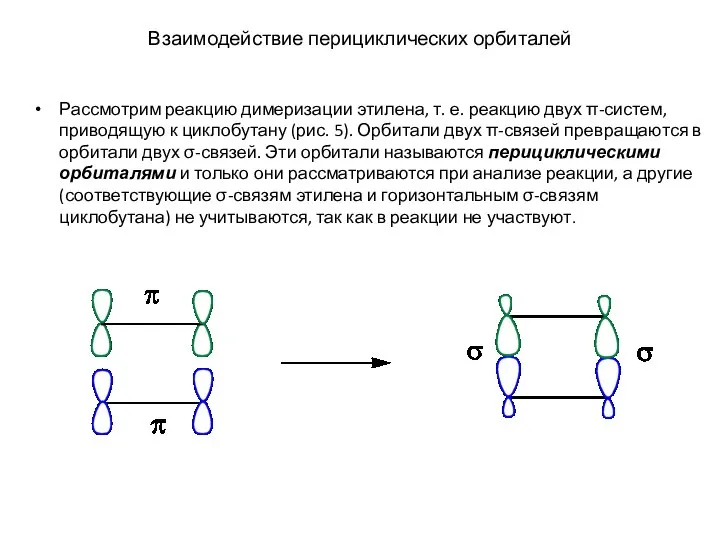
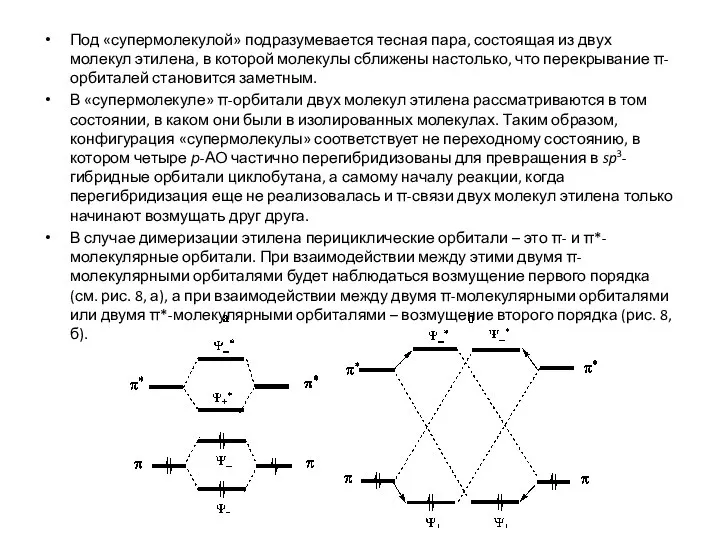
Взаимодействие перициклических орбиталей
Рассмотрим реакцию димеризации этилена, т. е. реакцию двух π-систем, приводящую к циклобутану (рис. 5). Орбитали двух π-связей превращаются в орбитали двух σ-связей. Эти орбитали называются перициклическими орбиталями и только они рассматриваются при анализе реакции, а другие (соответствующие σ-связям этилена и горизонтальным σ-связям циклобутана) не учитываются, так как в реакции не участвуют.

Перициклические орбитали – это орбитали образующихся и разрывающихся связей.
Возможность осуществления реакции при сближении двух молекул этилена связана с теми изменениями орбитальной энергии каждой молекулы, которые происходят при этом. К взаимодействию двух молекулярных орбиталей применимы все те же правила, что и к взаимодействию двух атомных орбиталей.
Из двух взаимодействующих базисных молекулярных орбиталей получаются две новые возмущенные молекулярные орбитали.
При этом возможны два варианта возмущения в зависимости от энергий базисных молекулярных орбиталей:
Базисные молекулярные орбитали имеют одинаковую энергию (рис. 6, а).
При возмущении таких молекулярных орбиталей образуются две новые возмущенные орбитали, причем
Ψ1 и Ψ2 – базисные молекулярные орбитали;
Ψ+ и Ψ_– возмущенные молекулярные орбитали «cупермолекулы».

Возмущение, описывающееся уравнениями (1), называется возмущением первого порядка.
Базисные молекулярные орбитали имеют разную энергию (рис. 6, б). При возмущении таких молекулярных орбиталей образуются две новые возмущенные орбитали, причем
где Ψ1 – базисная молекулярная орбиталь с более низкой энергией;
Ψ2 − базисная молекулярная орбиталь с более высокой энергией.
Важно, что чем больше разность энергий между Ψ1 и Ψ2, тем меньше возмущение при одинаковом перекрывании (λ → 0). При возмущении второго порядка и образовании возмущенной орбитали Ψ+ базисная молекулярная орбиталь Ψ2 подмешивается к базисной молекулярной орбитали Ψ1 (с коэффициентом λ), а при образовании Ψ_ базисная молекулярная орбиталь Ψ1 подмешивается к базисной молекулярной орбитали Ψ2 (также с коэффициентом λ). Другими словами, Ψ+ − это в основном Ψ1, а Ψ_ − в основном Ψ2.

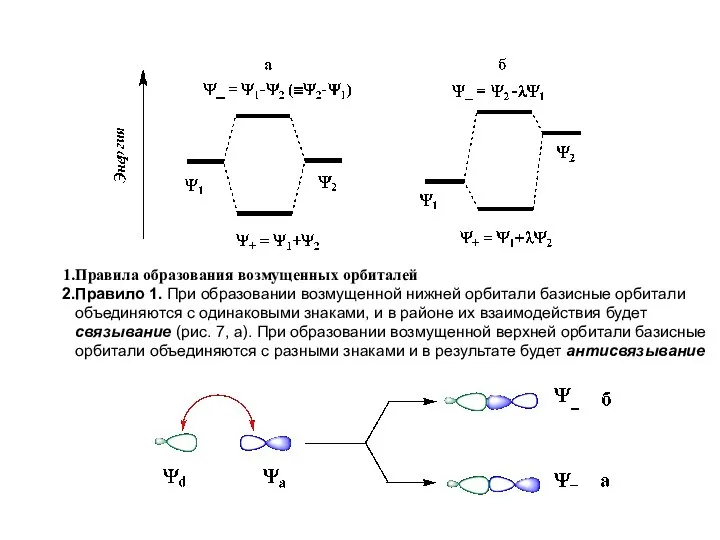
Правила образования возмущенных орбиталей
Правило 1. При образовании возмущенной нижней орбитали базисные орбитали объединяются с одинаковыми знаками, и в районе их взаимодействия будет связывание (рис. 7, а). При образовании возмущенной верхней орбитали базисные орбитали объединяются с разными знаками и в результате будет антисвязывание

Правило 2. Если возмущенные орбитали имеют разную энергию, возмущение приводит к тому, что энергия орбиталей, первоначально имеющих более низкую энергию, еще более понижается, а энергия орбиталей, имеющих первоначально более высокую энергию, еще более повышается. Такие изменения энергии наиболее выражены при максимальном перекрывании орбиталей и менее выражены при значительном различии между энергиями взаимодействующих орбиталей.
Правило 3. Орбиталь с первоначально более низкой энергией изменяется при частичном взаимодействии с орбиталью, которая имеет более высокую энергию, связывающим образом (в фазе). Орбиталь с первоначально более высокой энергией изменяется при частичном воздействии орбитали с низкой энергией антисвязывающим образом (в противофазе). В каждом случае взаимодействие тем лучше, чем больше перекрывание орбиталей, и тем меньше, чем больше начальная разница в энергии взаимодействующих орбиталей.
Применим эти правила к взаимодействию двух молекул этилена. В методе ВМО рассматривается лишь начальная стадия реакции, а продукт реакции не анализируется. Необходимо определить, будет ли стабильной «супермолекула» (СН2=СН2)2 по сравнению с парой молекул реагентов 2СН2=СН2.

Под «супермолекулой» подразумевается тесная пара, состоящая из двух молекул этилена, в которой молекулы сближены настолько, что перекрывание π-орбиталей становится заметным.
В «супермолекуле» π-орбитали двух молекул этилена рассматриваются в том состоянии, в каком они были в изолированных молекулах. Таким образом, конфигурация «супермолекулы» соответствует не переходному состоянию, в котором четыре р-АО частично перегибридизованы для превращения в sp3-гибридные орбитали циклобутана, а самому началу реакции, когда перегибридизация еще не реализовалась и π-связи двух молекул этилена только начинают возмущать друг друга.
В случае димеризации этилена перициклические орбитали – это π- и π*-молекулярные орбитали. При взаимодействии между этими двумя π-молекулярными орбиталями будет наблюдаться возмущение первого порядка (см. рис. 8, а), а при взаимодействии между двумя π-молекулярными орбиталями или двумя π*-молекулярными орбиталями – возмущение второго порядка (рис. 8, б).

Симметрия молекулярных орбиталей
2.2.1. Точечные группы симметрии
Операции симметрии, которые будут рассмотрены, таковы, что, по крайней мере, одна точка объекта остается неподвижной. Такие операции называются точечными, а неподвижная точка, которая не меняет положения при всех точечных операциях симметрии объекта, − это центр тяжести объекта, в котором пересекаются все оси и плоскости симметрии.
Каждой операции симметрии соответствует определенный элемент симметрии.
Элементом симметрии называется геометрическое место точек, остающихся неподвижными при данной операции симметрии.
Основными элементами симметрии являются:
собственные оси вращения, которые имеют символ Сn, (n-порядок оси, означающий, что поворот молекулы на угол 2π/n приводит к структуре, неотличимой от первоначальной);
несобственные оси вращения, или зеркально-поворотные оси (Sn);
зеркальные плоскости симметрии σ, делящие молекулу пополам так, что одна половина является зеркально-симметричной другой половине;
центр инверсии (i);
тождественное преобразование (E).

Собственная ось симметрии. Все молекулы имеют ось С1, поскольку в любом случае поворот на 360о возвращает молекулу в исходное состояние. Следовательно, операция С1 эквивалентна операции идентичности (С1≡Е).
Несобственная ось симметрии. Простейшая зеркально-поворотная ось S1 эквивалентна перпендикулярной ей плоскости симметрии (S1≡σ). Зеркально-поворотные оси более высокого порядка (Sn) можно рассматривать как комбинацию вращения на угол 2π/n с последующим отражением в плоскости, перпендикулярной оси вращения.
Симметрия – это основа теории МО. При операции симметрии произвольно выбранная точка внутри молекулы превращается в новую точку. Если они эквивалентны, то физическое состояние молекулы остается неизменным. В рамках теории МО этот вывод означает, что Ψ2, описывающая электронную плотность, должна быть в обеих точках одинаковой. Другими словами, функция Ψ2 должна обладать всеми элементами симметрии молекулы. Если рассматривается молекула с неcколькими элементами симметрии, то распределение электронов (Ψ2) на каждой молекулярной орбитали не должно меняться при всех операциях симметрии, которые могут быть произведены с точечной группой симметрии самой молекулы (т. е. с ядерным остовом). Только в этом случае молекулярно-орбитальное описание будет соответствовать реальному объекту.