Содержание
- 2. Математическая модель химического реактора включает два уравнения: - уравнение материального баланса - уравнение теплового баланса В
- 3. Уравнение материального баланса химического реактора Варианты: Общий (брутто-баланс) Частный баланс по компоненту Элементный баланс 3
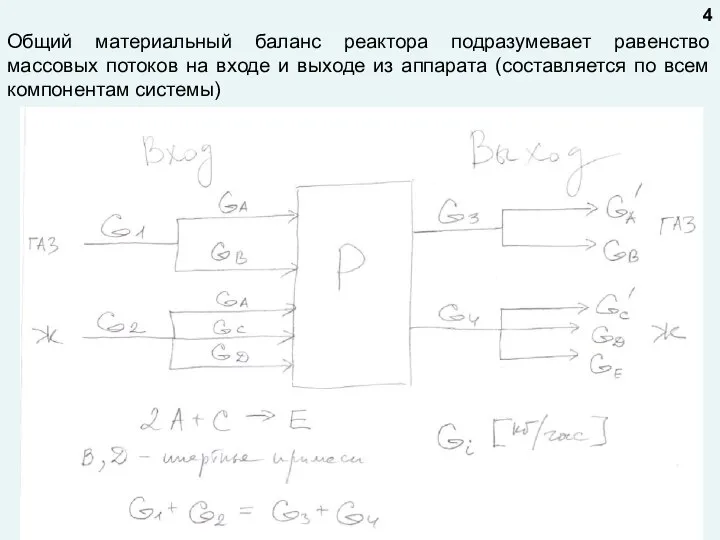
- 4. Общий материальный баланс реактора подразумевает равенство массовых потоков на входе и выходе из аппарата (составляется по
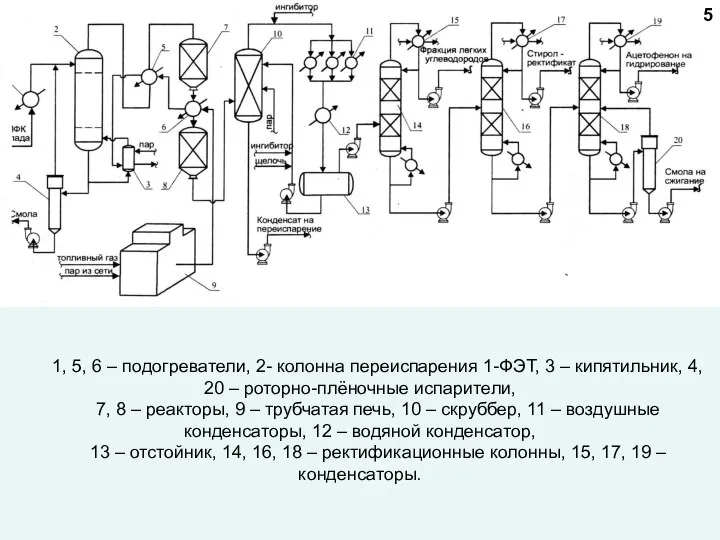
- 5. 1, 5, 6 – подогреватели, 2- колонна переиспарения 1-ФЭТ, 3 – кипятильник, 4, 20 – роторно-плёночные
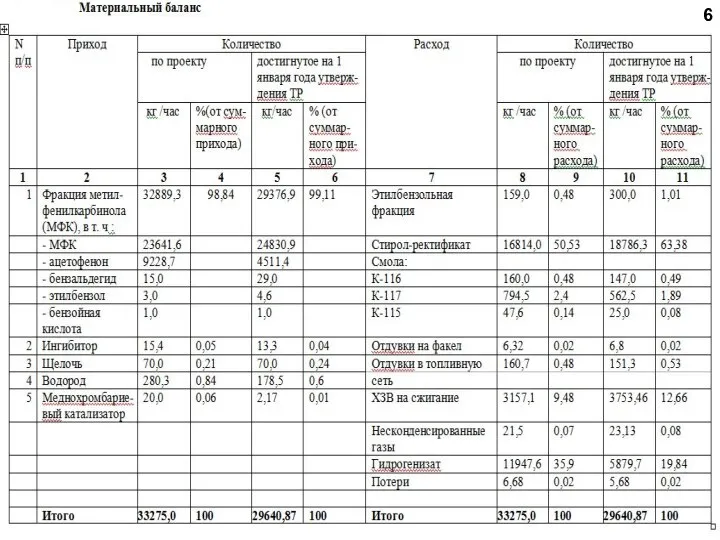
- 6. 6
- 7. Частный материальный баланс реактора по компоненту реакционной системы (реагенту или продукту) составляется с учетом расходования или
- 8. Элементный баланс может быть составлен по любому элементу, например: по углероду для органических смесей по азоту
- 9. Уравнение материального баланса для элементарного объема аппарата, в котором протекает химическая реакция: А → В где
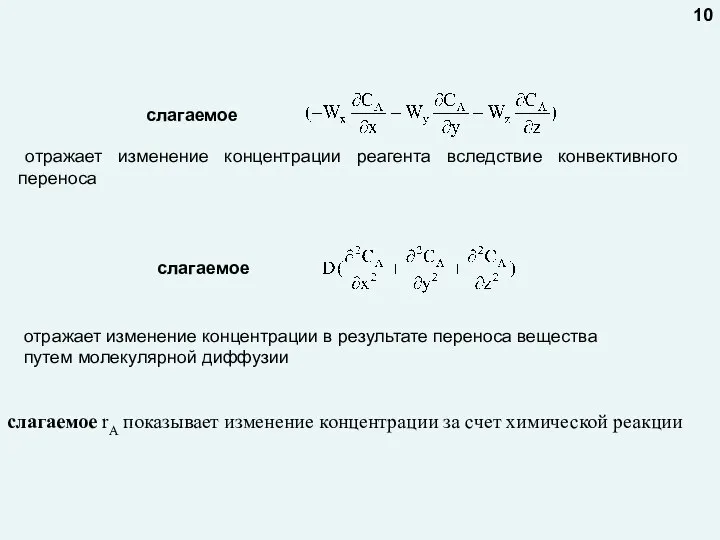
- 10. слагаемое отражает изменение концентрации реагента вследствие конвективного переноса слагаемое отражает изменение концентрации в результате переноса вещества
- 11. Гидродинамические модели реакторов. Вывод характеристических уравнений. Любой химический реактор в большем или меньшем приближении можно описать
- 12. Реактор идеального смешения периодического действия РИС-П Аппарат с мешалкой, в который периодически загружают исходные реагенты и
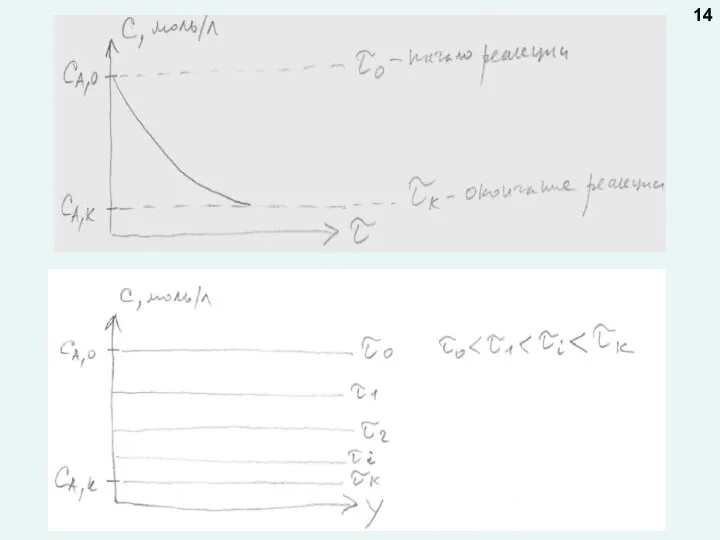
- 13. Графические зависимости: 1. Изменение концентрации реагента во времени СA=f(τ) 2. Изменение концентрации реагента по объему аппарата
- 14. 14
- 15. 15
- 16. При Vреакци.смеси = const CA = CA,0 (1-αА) - характеристическое уравнение РИС-П 16
- 17. Предположим, что в реакторе протекает простая необратимая реакция «n»-го порядка nA → продукты По закону действующих
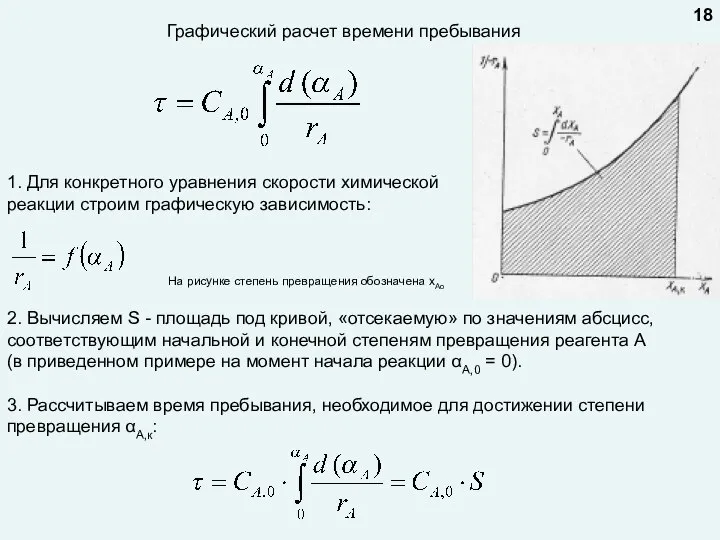
- 18. 1. Для конкретного уравнения скорости химической реакции строим графическую зависимость: Графический расчет времени пребывания 2. Вычисляем
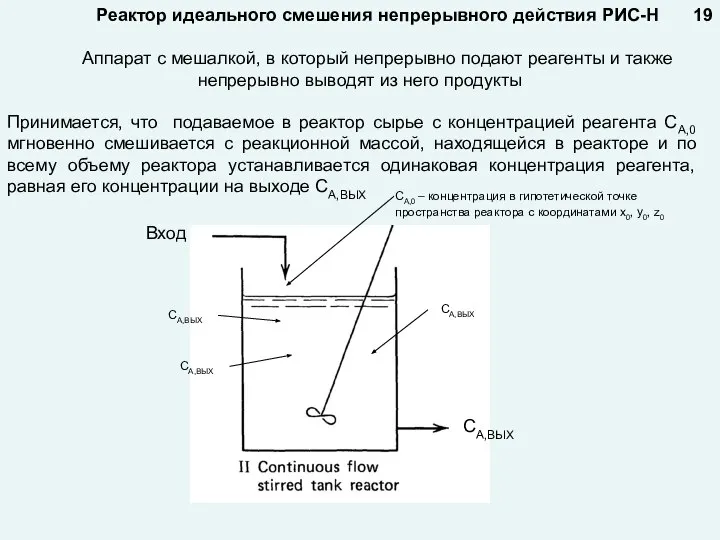
- 19. Реактор идеального смешения непрерывного действия РИС-Н Аппарат с мешалкой, в который непрерывно подают реагенты и также
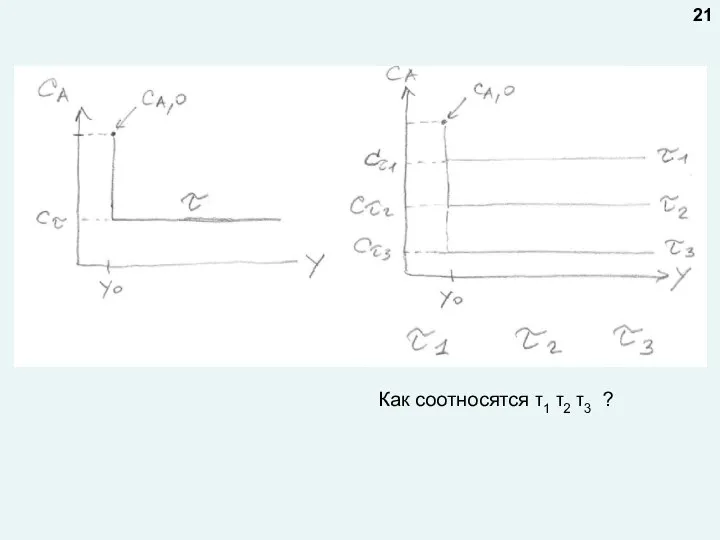
- 20. Графические зависимости: Изменение концентрации реагента по объему аппарата для времени пребывания (реакции) τ (беря по абсциссе
- 21. Как соотносятся τ1 τ2 τ3 ? 21
- 22. 22
- 23. Поскольку для РИС-Н (работающего в стационарном режиме) характерно отсутствие градиента параметров и во времени, и по
- 24. - характеристическое уравнение для РИС-Н 24
- 25. Предположим, что в реакторе протекает простая необратимая реакция «n»-го порядка nA → продукты По закону действующих
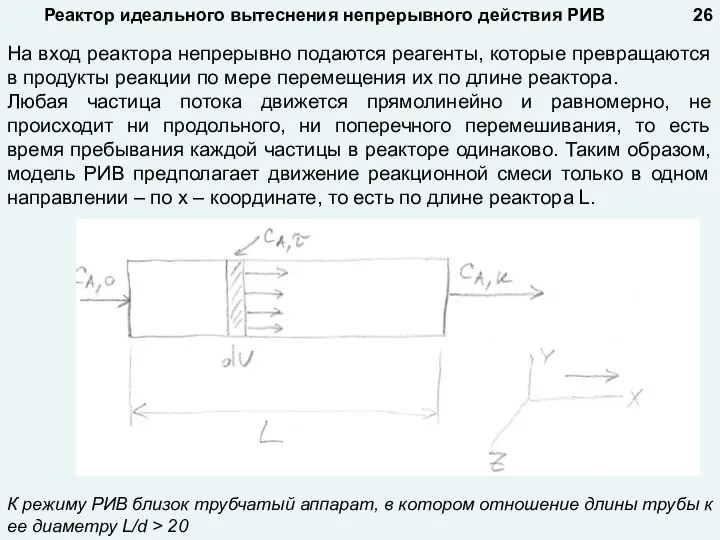
- 26. Реактор идеального вытеснения непрерывного действия РИВ К режиму РИВ близок трубчатый аппарат, в котором отношение длины
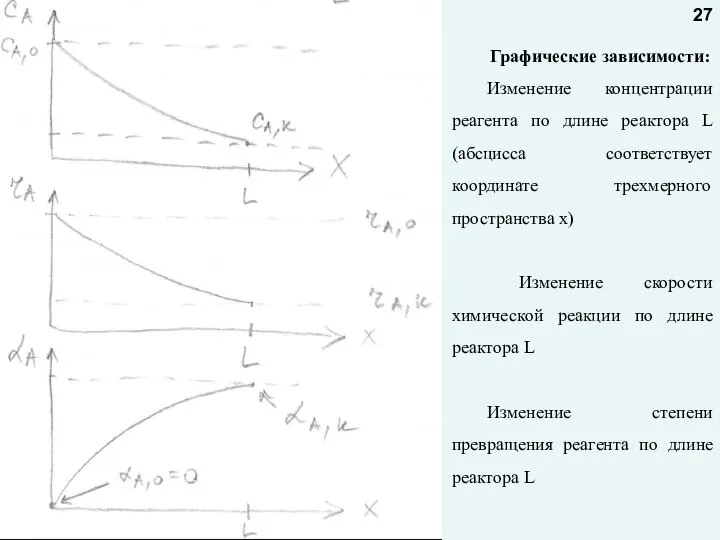
- 27. Графические зависимости: Изменение концентрации реагента по длине реактора L (абсцисса соответствует координате трехмерного пространства x) Изменение
- 28. Так как изменение концентрации происходит только в одном направлении - по длине реактора, а составляющие конвективного
- 29. С учетом вышеизложенного получаем для реактора РИВ уравнение материального баланса в виде: Как было отмечено выше,
- 30. Линейная скорость движения реакционной смеси в реакторе с постоянной площадью сечения равна С учетом этого уравнение
- 31. Как видно, характеристические уравнения материального баланса для РИС-П и РИВ одинаковы, то есть время достижения заданной
- 32. Сравнение РИС-Н и РИВ В РИС-Н вспомогательных операций нет, как и в случае РИВ, но гидродинамическая
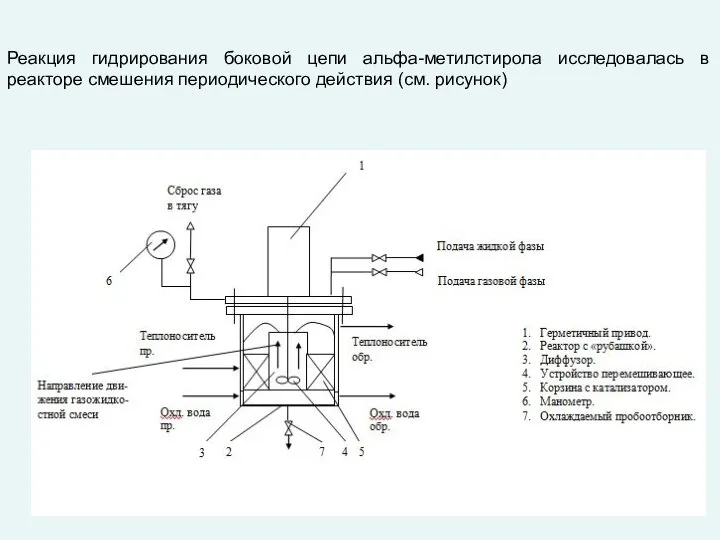
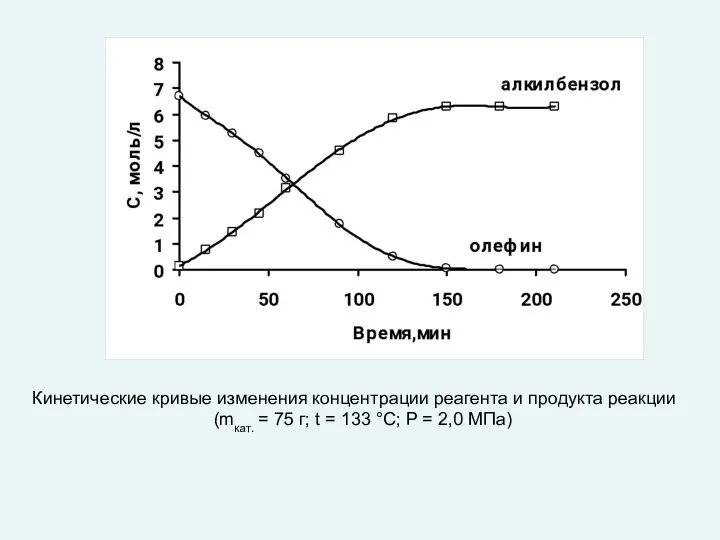
- 33. Реакция гидрирования боковой цепи альфа-метилстирола исследовалась в реакторе смешения периодического действия (см. рисунок)
- 35. Общий вид кинетического уравнения в соответствии с законом действующих масс где kэфф. - эффективная константа скорости,
- 36. Кинетические кривые изменения концентрации реагента и продукта реакции (mкат. = 75 г; t = 133 °С;
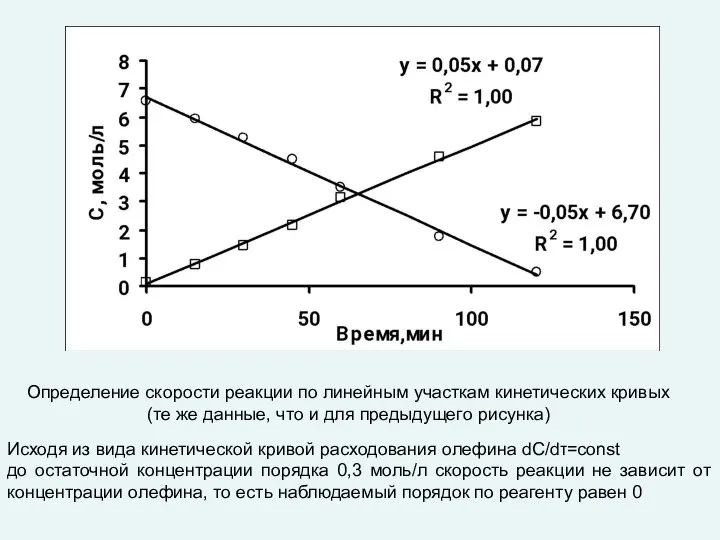
- 37. Определение скорости реакции по линейным участкам кинетических кривых (те же данные, что и для предыдущего рисунка)
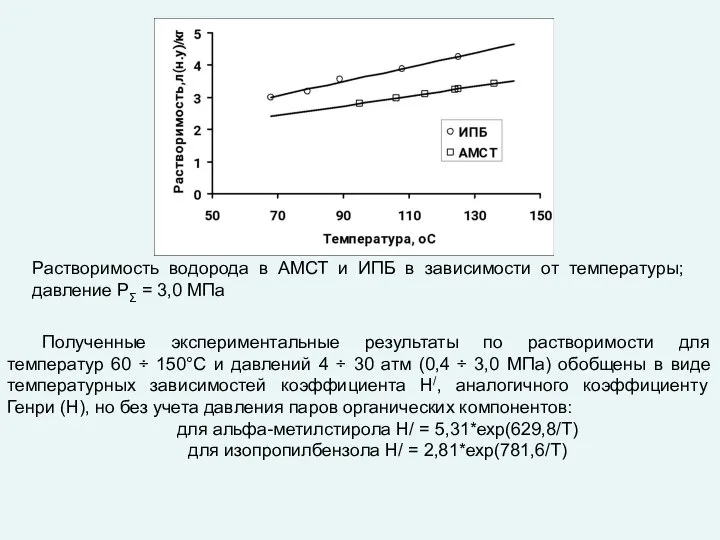
- 38. Растворимость водорода в АМСТ и ИПБ в зависимости от температуры; давление PΣ = 3,0 МПа Полученные
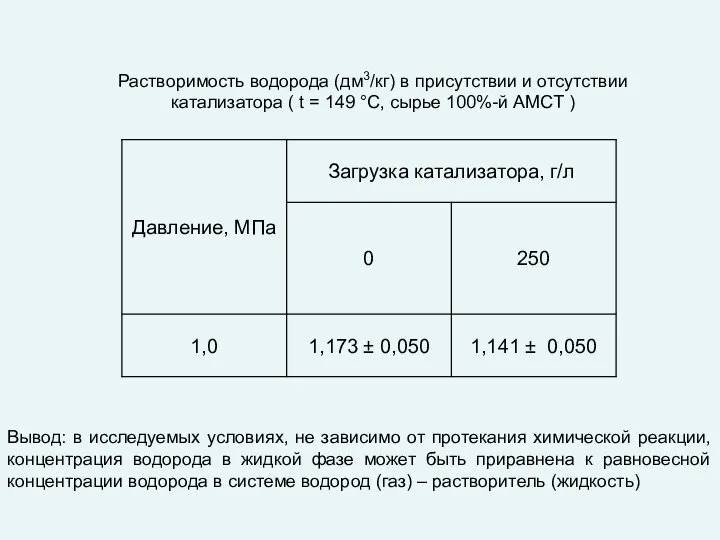
- 39. Растворимость водорода (дм3/кг) в присутствии и отсутствии катализатора ( t = 149 °С, сырье 100%-й АМСТ
- 40. К определению порядка по водороду: логарифм скорости гидрирования альфа-метилстирола в зависимости от логарифма концентрации водорода в
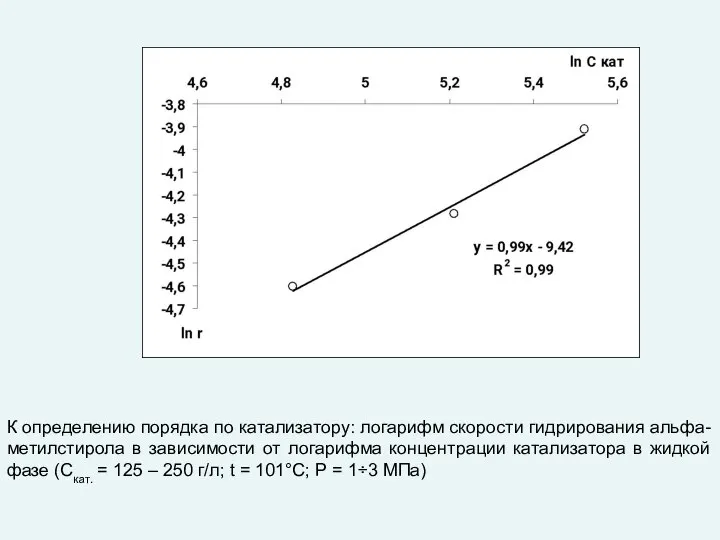
- 41. К определению порядка по катализатору: логарифм скорости гидрирования альфа-метилстирола в зависимости от логарифма концентрации катализатора в
- 42. Итого: порядок по олефину принимаем равным 0 порядок по водороду принимаем равным 1 порядок по катализатору
- 43. Как определяются параметры уравнения Аррениуса kэфф,0 и ЕА Проводится серия экспериментов в изотермических условиях, когда переменной
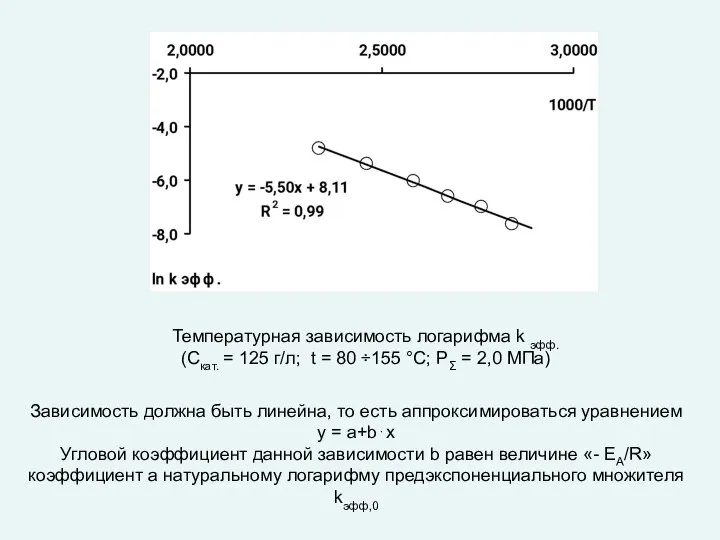
- 44. Температурная зависимость логарифма k эфф. (Cкат. = 125 г/л; t = 80 ÷155 °С; РΣ =
- 45. Итоговое кинетическое уравнение скорости химической реакции:
- 47. Скачать презентацию


























 Электронная конфигурация атома
Электронная конфигурация атома Движение молекул
Движение молекул L4_Aminoacids, peptides, proteins (2)
L4_Aminoacids, peptides, proteins (2) Простые вещества - неметаллы
Простые вещества - неметаллы Введение в общую теорию поверхностных явлений. Лекция 1
Введение в общую теорию поверхностных явлений. Лекция 1 Приемы разделения мембранных липидов на классы
Приемы разделения мембранных липидов на классы Оксиды
Оксиды Простое вещество и химический элемент азот
Простое вещество и химический элемент азот Презентация на тему Органическая химия "Жиры"
Презентация на тему Органическая химия "Жиры"  Валентность
Валентность Презентация по Химии "Углекислый газ"
Презентация по Химии "Углекислый газ"  Природные источники углеводородов
Природные источники углеводородов Арены. Бензол
Арены. Бензол Алканы
Алканы Алкены
Алкены Презентация на тему Великие химики
Презентация на тему Великие химики  proekt_TTU_15 (1)
proekt_TTU_15 (1) Термохимическое уравнение реакции полного сгорания ацетилена
Термохимическое уравнение реакции полного сгорания ацетилена Презентация на тему Химия и стирка
Презентация на тему Химия и стирка  Предельные и непредельные углеводороды
Предельные и непредельные углеводороды Презентация на тему Пестициды
Презентация на тему Пестициды  Презентация на тему Щелочные металлы
Презентация на тему Щелочные металлы  Спирты
Спирты Примеры реакций в жизни и в быту. Реакции по направлению процесса
Примеры реакций в жизни и в быту. Реакции по направлению процесса Химические явления
Химические явления Химическая связь
Химическая связь Актиний. Нахождение в природе
Актиний. Нахождение в природе Метиловый спирт
Метиловый спирт