Жидкокристаллический эластомер как роторный актуатор

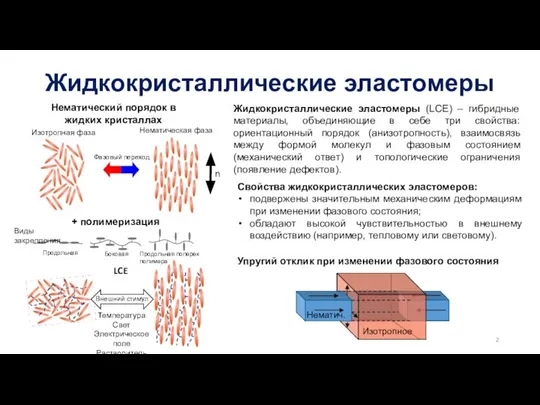
Жидкокристаллические эластомеры
Нематический порядок в жидких кристаллах
Изотропная фаза
Нематическая фаза
n
+ полимеризация
Внешний стимул
Температура
Свет
Электрическое поле
Растворитель
Фазовый переход
Продольная
Боковая
Продольная поперек полимера
LCE
Жидкокристаллические эластомеры (LCE) – гибридные материалы, объединяющие в себе три свойства: ориентационный порядок (анизотропность), взаимосвязь между формой молекул и фазовым состоянием (механический ответ) и топологические ограничения (появление дефектов).
2
Свойства жидкокристаллических эластомеров:
подвержены значительным механическим деформациям при изменении фазового состояния;
обладают высокой чувствительностью в внешнему воздействию (например, тепловому или световому).
Упругий отклик при изменении фазового состояния
Изотропное
Нематич.
Виды закрепления

LCE актуаторы
Теплом
Актуация может быть вызвана:
Светом
Serak et al., Soft Matter 6, 779-783 (2010)
Растворитель (LC гель)
Hashimoto et al., Ang. Chem. 47, 6690-6693 (2008)
Finkelmann, e-Polymers 1, 111-123 (2001)
Перистальтическое движение
Hashimoto et al.,
Adv.Materials 19.21 (2007)
Самостоятельное перемещение
Актуатор – универсальное исполнительное устройство. Им может быть как некоторое устройство, так и материал.
Под актуацией понимается приведение актуатора в возбужденное состояние или смена его состояния.

DEA роторный микромотор
Структура DEA роторного микромотора
Схема работы DEA роторного микромотора
Imboden, Ji et al. DEA Rotary micro-motor (https://lmts.epfl.ch/EAPmotor)

Мотор Икеды
Ikeda et al. Angew. Chem., 120, 5064 –5066 (2008)
Конструкция мотора:
Мотор представляет собой систему шкивов, на которую помещена LCE-пленка в форме ремня.
Принцип работы мотора:
Часть LCE-пленки на правом шкиве освещается ультрафиолетом. В результате возникает локальная сила сжатия.
Часть LCE-пленки на левом шкиве освещается видимым светом. В результате возникает локальная сила растяжения.
Одновременное воздействие видимого света и ультрафиолета приводит к вращению системы шкивов.

Эксперимент
Тонкая пленка нематического эластомера
Лазер циклически сканирует и локально нагревает эластомер
При воздействии лазера эластомер сгибается (т.к. анизотропен по толщине – принцип термостата)
Время остывания > время нагрева
Трение о подложку может быть изменено (на видео бумага)
Hao Zeng (Tampere University of Technology, Finland)

Цель работы
Схема роторного мотора № 1
Изучение динамических свойств жидкокристаллических эластомеров, подверженных значительным механическим деформациям при изменении фазового состояния.
Конструкция мотора:
Мотор состоит из двух кольцевых и n радиальных активных нитей, соединённых в форму диска.
Внутреннее кольцо жестко закреплено на поворотном стержне и может только вращаться вокруг центра стержня.
Внешнее кольцо и радиальные нити ограничены в деформации только сохранением целостностью структуры и актуацией.
Вся конструкция находится на подложке.
Принцип работы:
Циклическая активация структуры из активных и пассивных нитей приводит к выполнению механической работы за счет деформаций и силы трения между конструкцией и подложкой.

Динамика роторного мотора
Предполагается:
нить при осевом сжатии изгибается, а не остается прямой, изменяя свою длину;
процесс актуации быстрее, чем процесс деактивации;
актуация производится с постоянной угловой скоростью ω;
актуация однородна в поперечном и продольном направлении нитей;
на каждом шаге вращения луча активации система приходит в равновесное состояние.
Недеформированное состояние
Последовательное воздействие луча активации на радиальные нити; нити, на которые в данный момент действует луч, окрашены красным цветом

Деформирование активных нитей

Расчет формы структуры
Расчет формы структуры производится с учетом того, что на каждом шаге поворота луча активации структура приходит к равновесному состоянию, удовлетворяя условию
– координаты системы
Поскольку характерное время релаксации намного меньше чем характерное время вращения луча, задача минимизации общей энергии для поиска равновесных состояний решалась на каждом шаге поворота луча следуя уравнению псевдо-эволюции системы
Энергия эластичности
Энергия осевой деформации
Энергия изгиба
Выражение для расчета кривизны κ

Алгоритм расчета
Установить положение луча активации на i-ой радиальной нити в текущий момент времени t.
Вычислить распределение
и вычислить оптимальные длины нитей.
Найти равновесное состояние, решив задачу минимизации энергии:
Вычислить изменение энергии из-за малого виртуального перемещения для каждого узла на внешнем кольце вокруг оси вращения в радиальном направлении и в нормальном направлении к плоскости структуры;
Вычислите изменение энергии из-за малого виртуального перемещения внутреннего кольца как твердого тела вокруг оси вращения;
Найти новые положения узлов согласно методу градиентного спуска
где γ мало, и одновременно обновлять все координаты узлов;

Алгоритм расчета
Выполнять шаги 3 а-с до тех пор, пока не приблизимся к минимуму энергии эластичности:
Сделать шаг по времени, переместив луч активации на i+1 – ю радиальную нить.
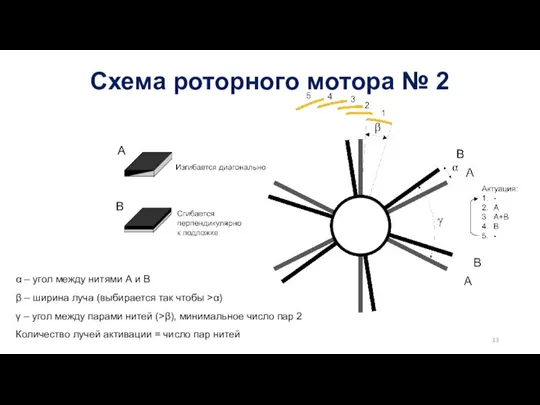
Повторить шаги 1 – 3.
Схема роторного мотора до начала актуации
Схема роторного мотора после одного цикла при k=0,5

Схема роторного мотора № 2
α – угол между нитями А и В
β – ширина луча (выбирается так чтобы >α)
γ – угол между парами нитей (>β), минимальное число пар 2
Количество лучей активации = число пар нитей