Расчетная ячейка при МД моделировании. Граничные условия. Элементарная ячейка для атомов аргона

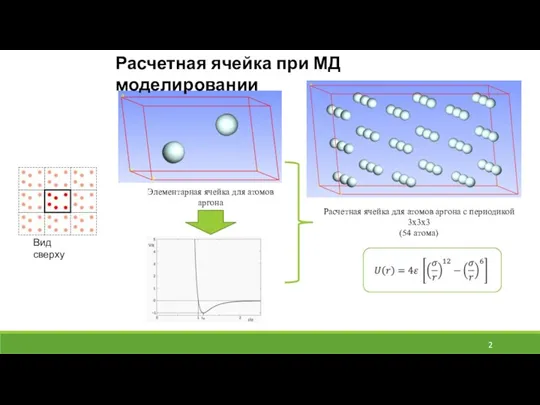
Элементарная ячейка для атомов аргона
Расчетная ячейка для атомов аргона с периодикой 3х3х3
(54 атома)
Расчетная ячейка при МД моделировании
Вид сверху

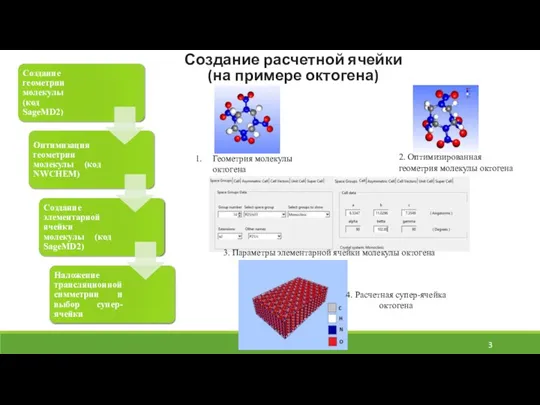
Создание расчетной ячейки
(на примере октогена)
Геометрия молекулы октогена
2. Оптимизированная геометрия молекулы октогена
3. Параметры элементарной ячейки молекулы октогена
4. Расчетная супер-ячейка октогена

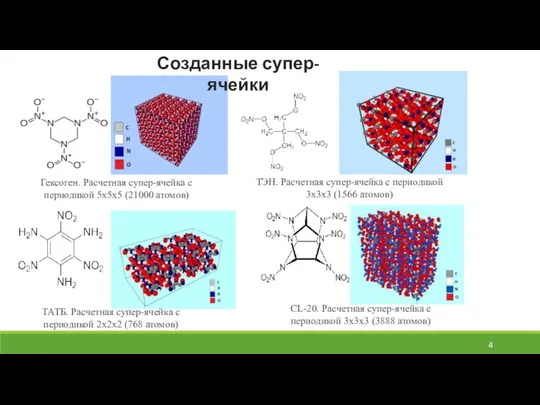
Созданные супер-ячейки
Гексоген. Расчетная супер-ячейка с периодикой 5х5х5 (21000 атомов)
ТЭН. Расчетная супер-ячейка с периодикой 3х3х3 (1566 атомов)
ТАТБ. Расчетная супер-ячейка с периодикой 2х2х2 (768 атомов)
CL-20. Расчетная супер-ячейка с периодикой 3х3х3 (3888 атомов)

Расчетная ячейка для MD моделирования распространения ударной волны в кристаллической решетке гексогена
Число атомов – 483840
Число молекул - 23040
Супер ячейка 80x6x6
Параметры ячейки:
a= 1344 Ǻ, b= 71 Ǻ, с= 66 Ǻ

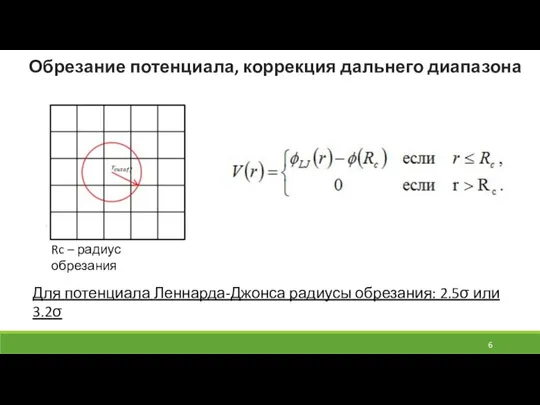
Обрезание потенциала, коррекция дальнего диапазона
Rc – радиус обрезания
Для потенциала Леннарда-Джонса радиусы обрезания: 2.5σ или 3.2σ

Периодические граничные условия
rс – координата атома в боксе
l,m,n - целые числа,
a, b, c - векторы, соответствующие граням бокса
rс + la + mb +nc, (l,m,n=-∞,∞)

Критерий минимального образа
Rc - радиуса обрезания
2Rс - размер бокса по каждому направлению

Типы непериодических граничных условий:
fixed ;
shrink-wrapped;
shrink-wrapped with a minimum value.
Непериодические граничные условия
Используются, когда необходимо читывать поверхностные эффекты:
модель пластины;
модель замороженного слоя;
проволочная модель.

МД моделирование для ансамблей частиц с постоянной температурой и постоянным давлением

Статистические ансамбли

Поддержание постоянной термодинамической величины
Различают 4 основных способа поддержания постоянной термодинамической величины:
Дифференциальный, когда величина имеет строго фиксированное значение, и флуктуации около среднего отсутствуют.
2. Пропорциональный, когда величины, связанные с термодинамической величиной f, корректируются на каждом шаге интегрирования с использованием поправочного коэффициента, устанавливающего заданное значение f. Поправочный коэффициент определяет величину флуктуаций вокруг
.
3. Интегральный, когда гамильтониан системы расширяется путем включения новых независимых величин, которые отражают эффект внешней среды, фиксирующей состояние желаемого ансамбля. Эволюция во времени этих величин описывается уравнениями движения, полученными из расширенного гамильтониана.
4. Стохастический, когда значения величин, связанных с термодинамической величиной f, присваиваются в соответствии с модифицированными уравнениями движения, в которых некоторые степени свободы дополнительно изменяются стохастически, чтобы придать желаемое среднее значение величине f.

Термостатирование
Термостат Берендсена
где T – текущее значение температуры (в момент времени t ),
– температура термостата,
– характерное время взаимодействия с резервуаром.
– коэффициент пересчета скоростей

Термостатирование
2. Термостат Андерсена
- Вероятность для каждого атома системы
- Вероятность следующей иттерации для каждого атома системы
- времена между виртуальными «столкновениями» для i-ого атома,
- полученный, с помощью генератора случайных чисел n-ый набор скоростей для соответствующего атома

Термостатирование
3. Термостат Ланжевена
- Случайная сила, вызывающая нагрев частиц
- Дисперсия
- Сила трения для компенсации температур

4. Термостат Нозе-Хувера
Термостатирование