Содержание
- 2. Концентрационный треугольник Решаются две задачи: а) по положению фигуративной точки тройного сплава на плоскости концентрационного треугольника
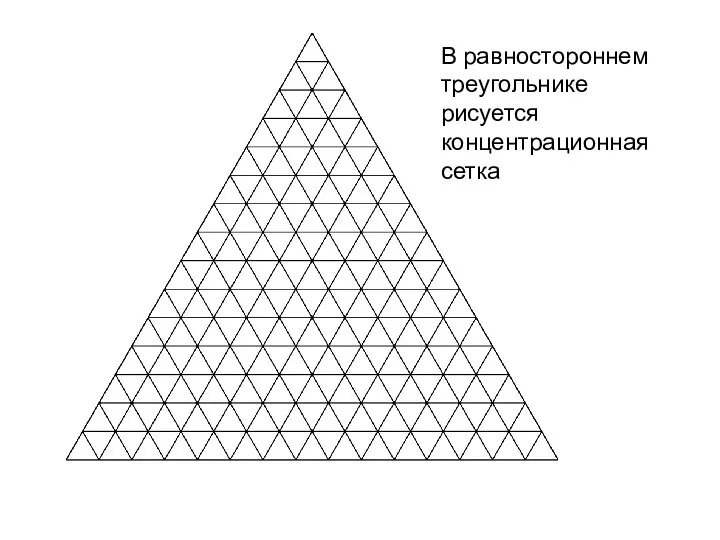
- 3. В равностороннем треугольнике рисуется концентрационная сетка
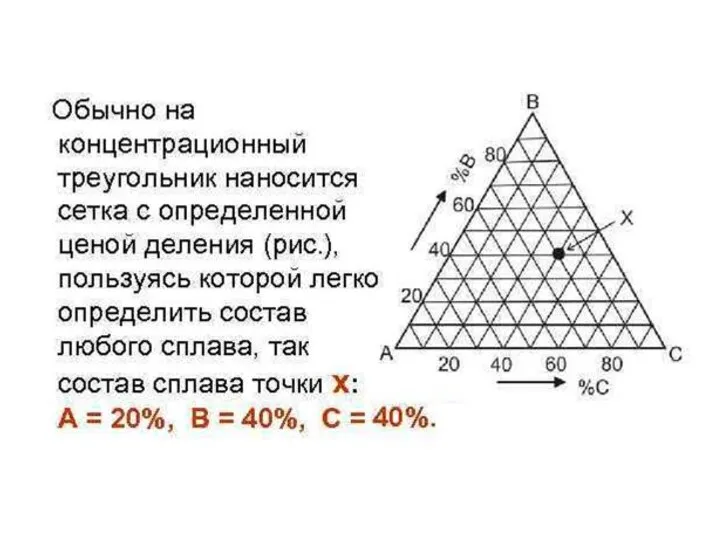
- 4. Составы трехкомпонентных сплавов указываются точкой на плоскости треугольника. Для опреде-ления этой точки исходят из концентрационных осей
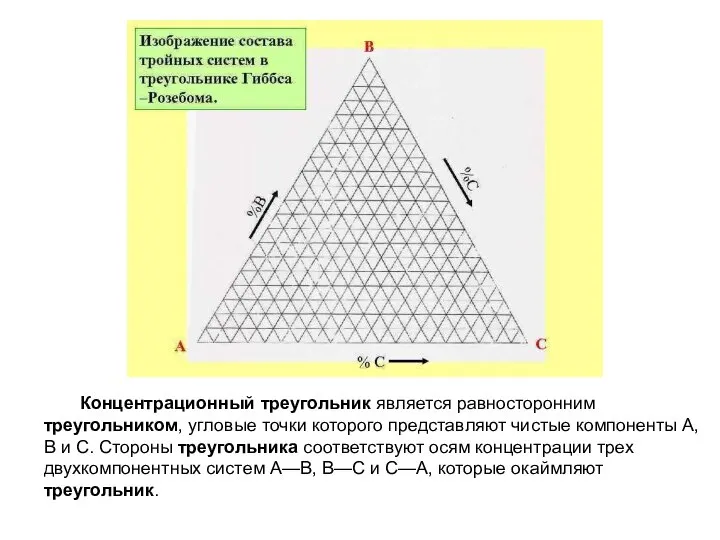
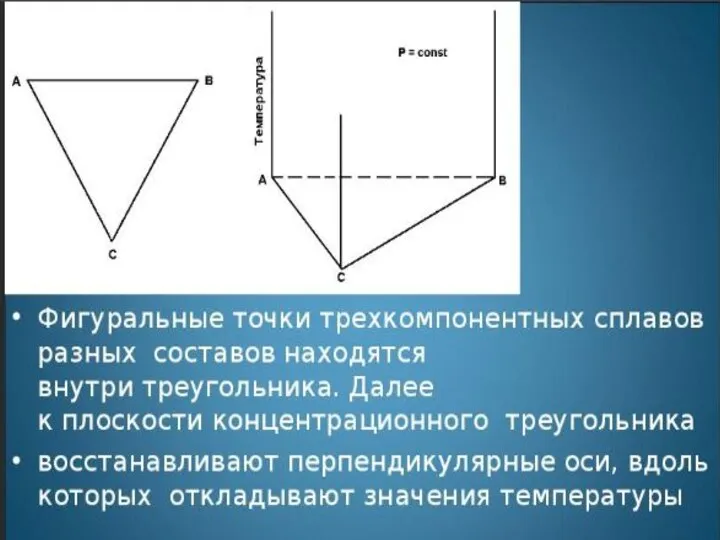
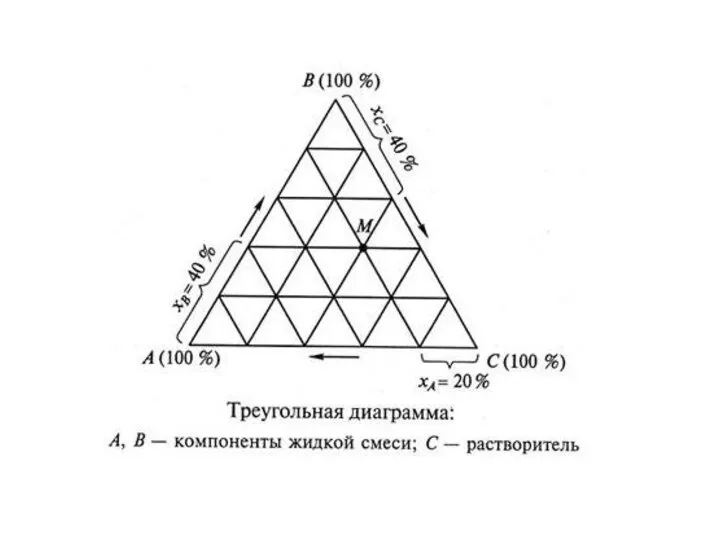
- 5. Концентрационный треугольник является равносторонним треугольником, угловые точки которого представляют чистые компоненты А, В и С. Стороны
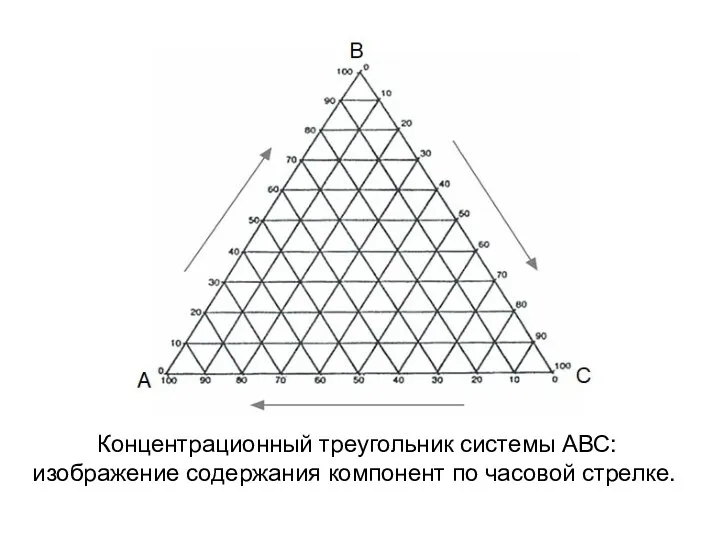
- 7. Концентрационный треугольник системы АВС: изображение содержания компонент по часовой стрелке.
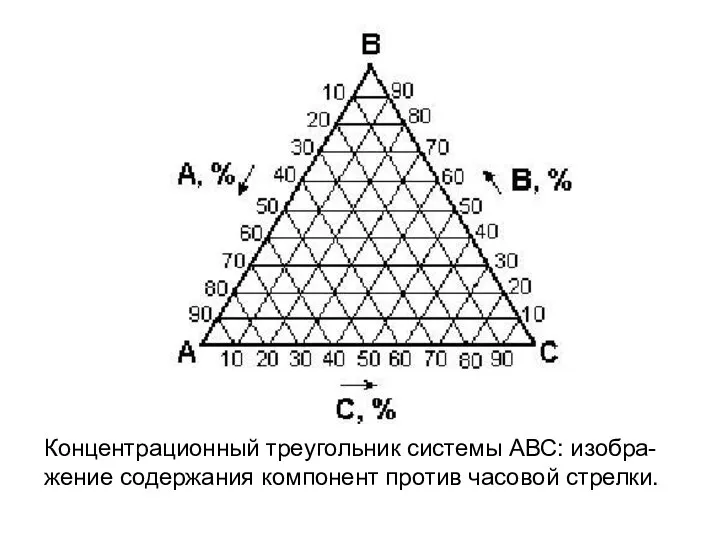
- 8. Концентрационный треугольник системы АВС: изобра-жение содержания компонент против часовой стрелки.
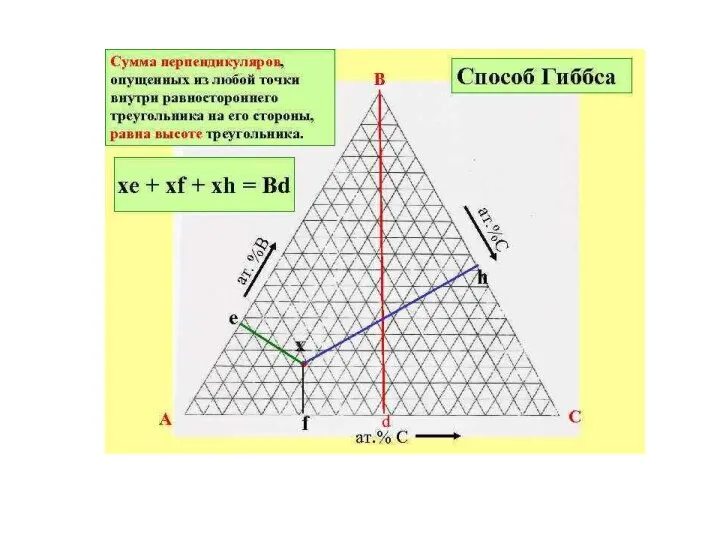
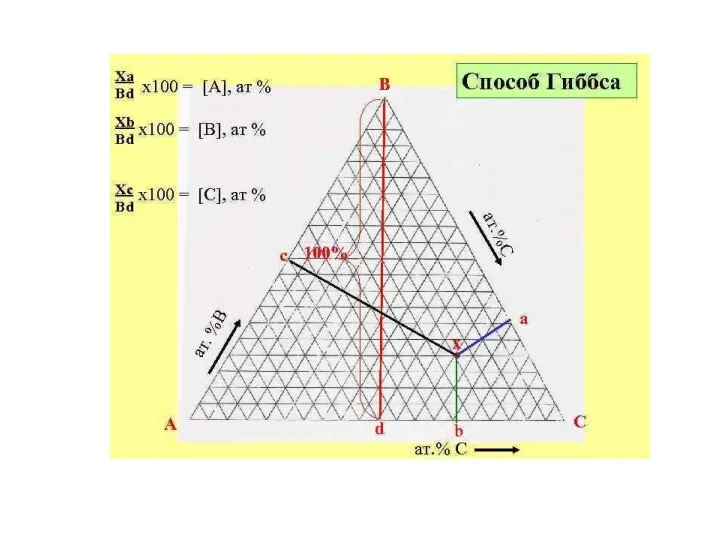
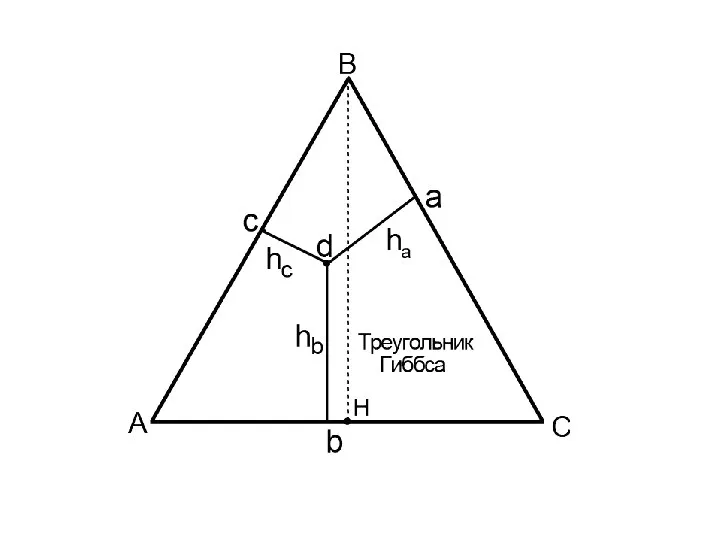
- 10. Треугольник Гиббса. Этот способ определяется тем, что сумма перпендикуляров, опущенных из любой точки внутри треугольника на
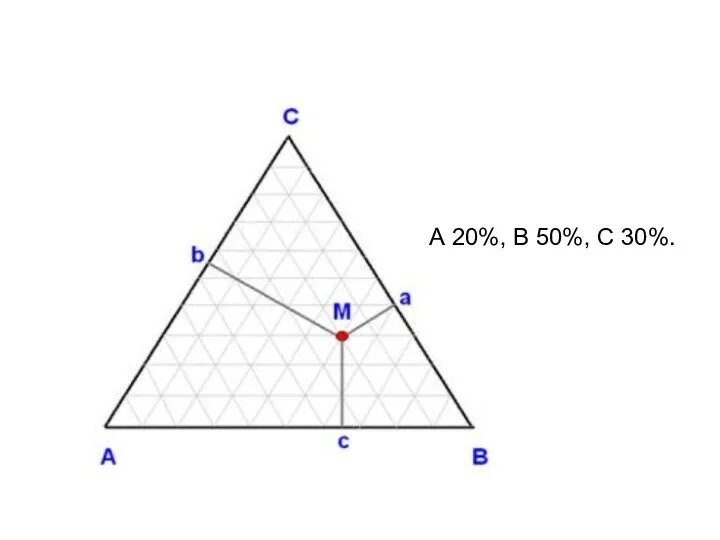
- 11. А 20%, В 50%, С 30%.
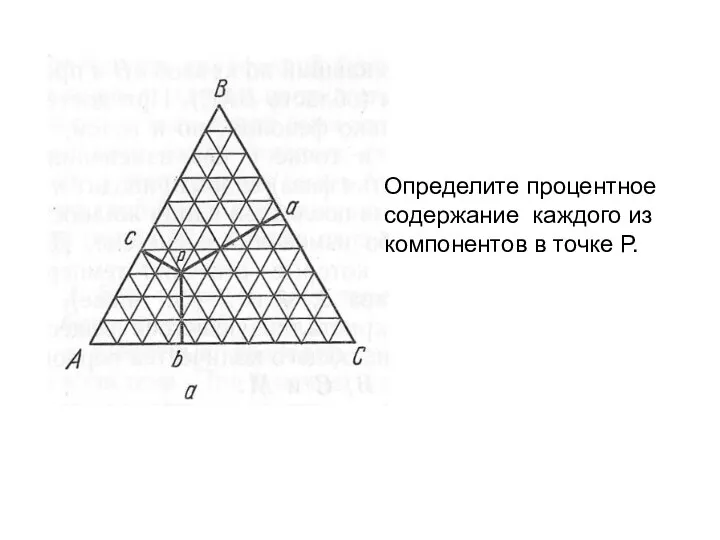
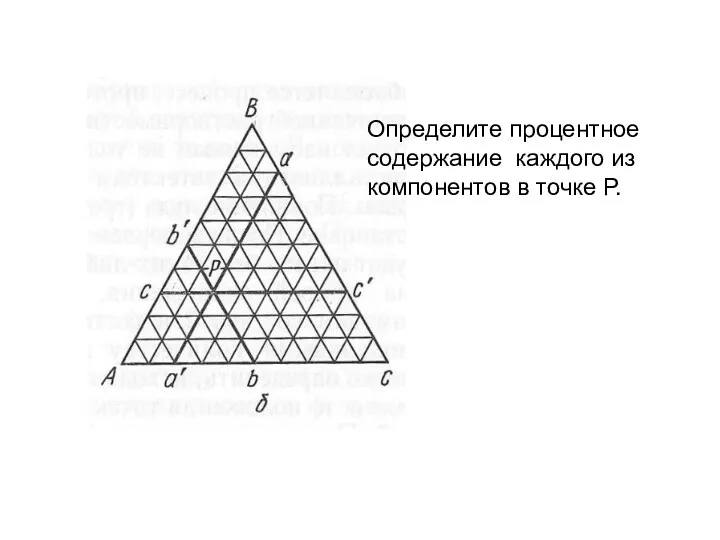
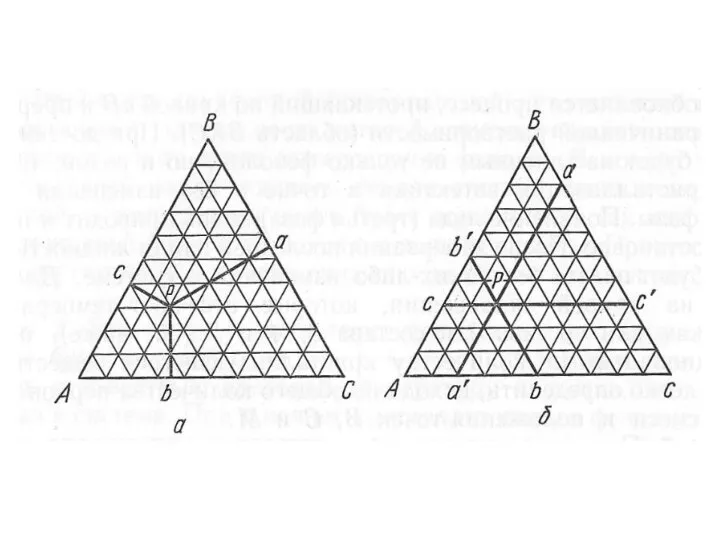
- 16. Определите процентное содержание каждого из компонентов в точке Р.
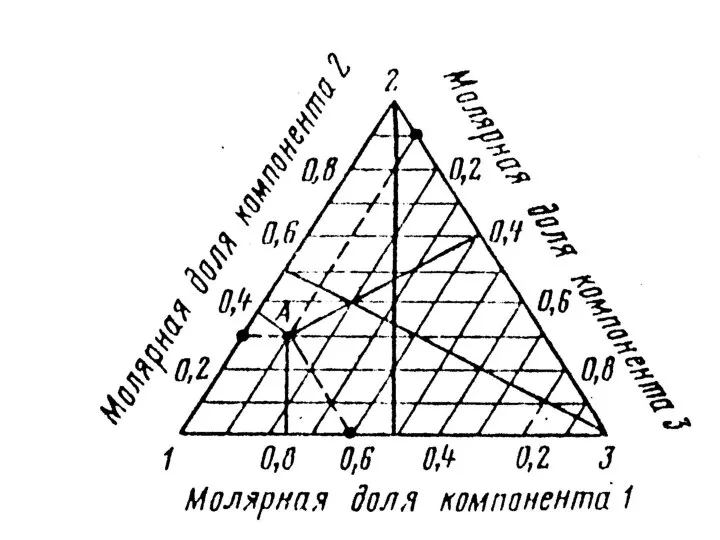
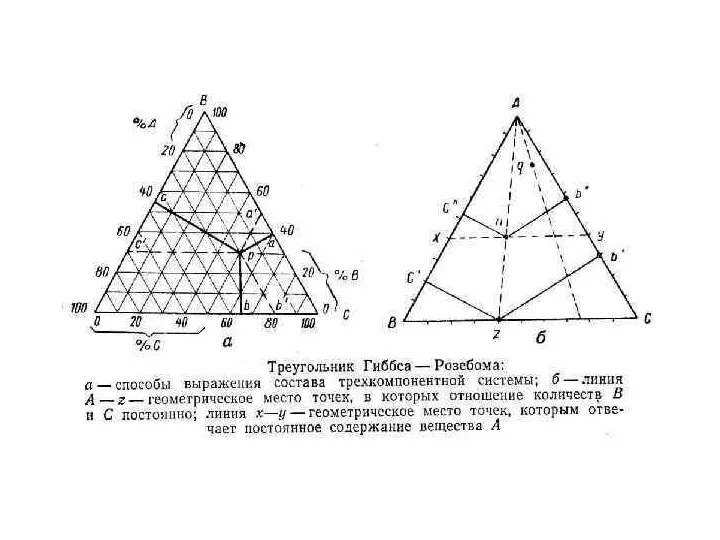
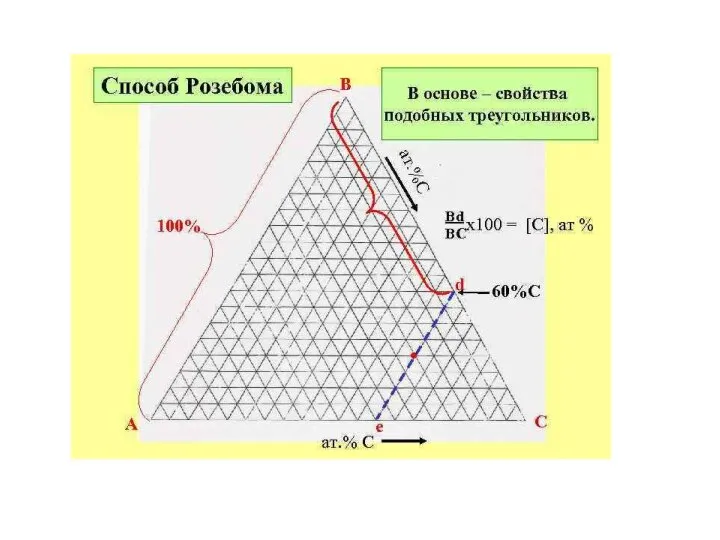
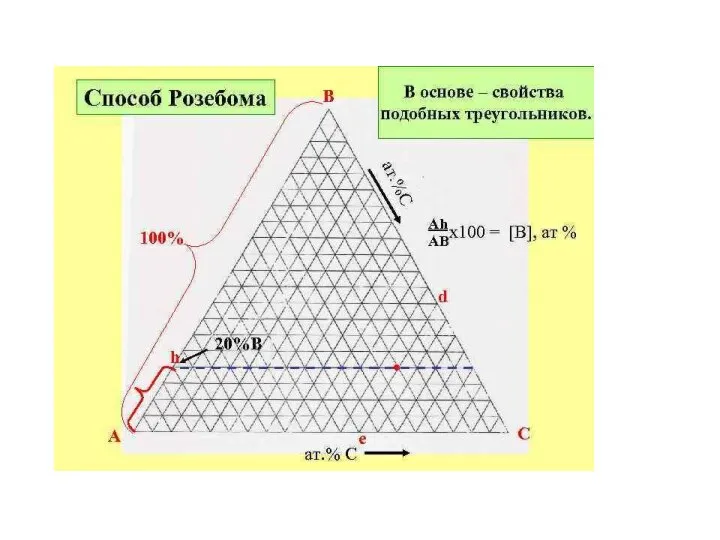
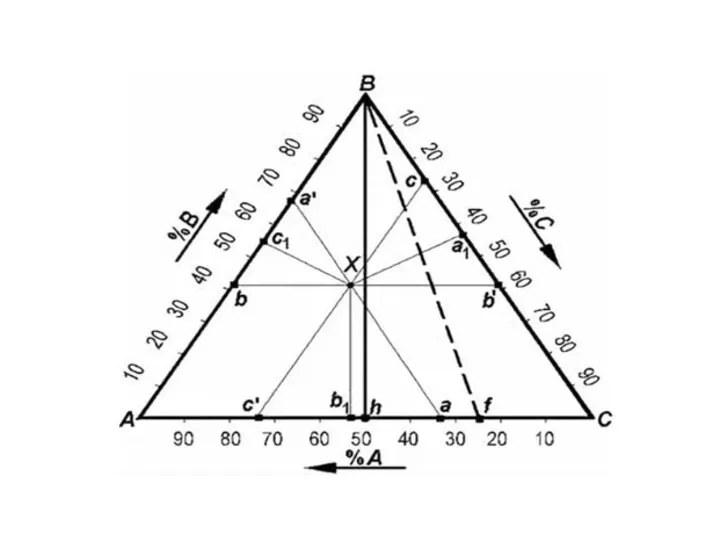
- 19. Треугольник Розебома. В этом способе за 100% принимают сторону треугольника и наносят сетку линий, параллельных каждой
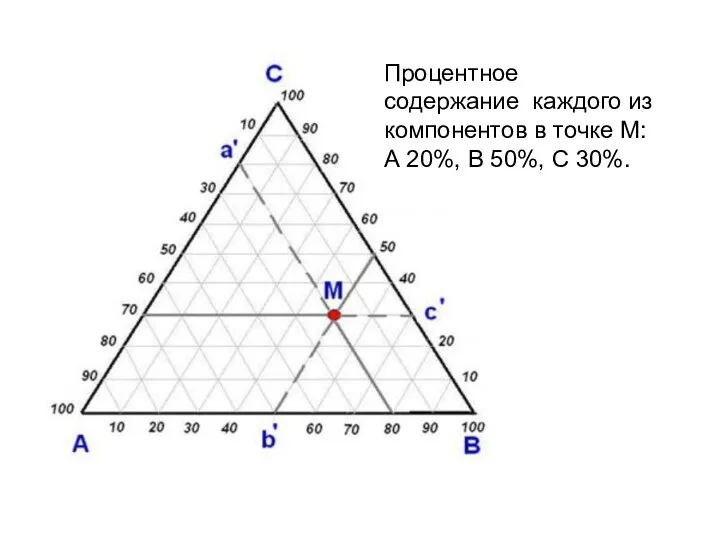
- 20. Процентное содержание каждого из компонентов в точке М: А 20%, В 50%, С 30%.
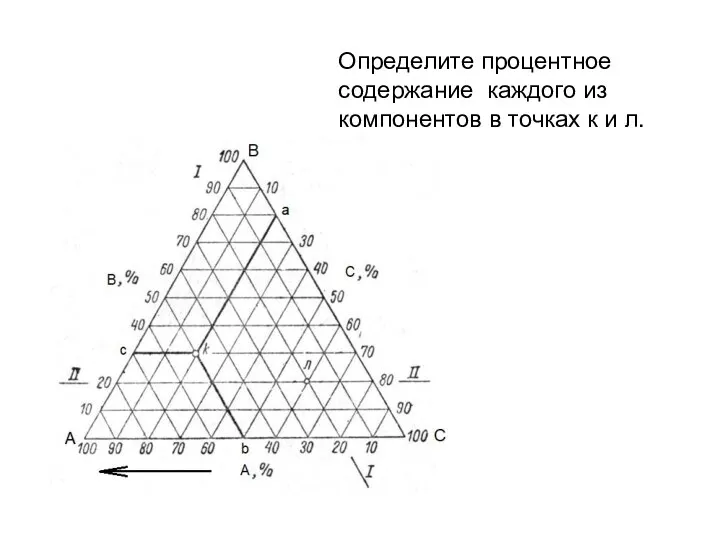
- 21. Определите процентное содержание каждого из компонентов в точках к и л.
- 22. Определите процентное содержание каждого из компонентов в точке Р.
- 24. Отметим три важных свойства линий (проекций) внутри треугольника Розебома. Линии, параллельные одной из сторон треуголь-ника, представляют
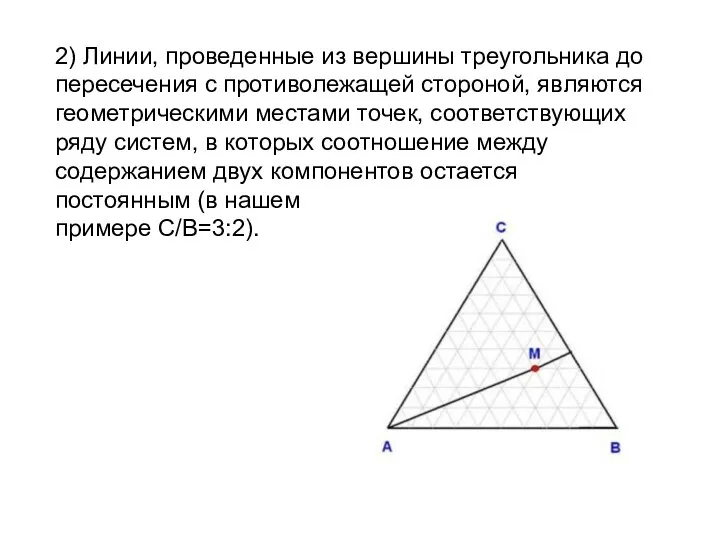
- 25. 2) Линии, проведенные из вершины треугольника до пересечения с противолежащей стороной, являются геометрическими местами точек, соответствующих
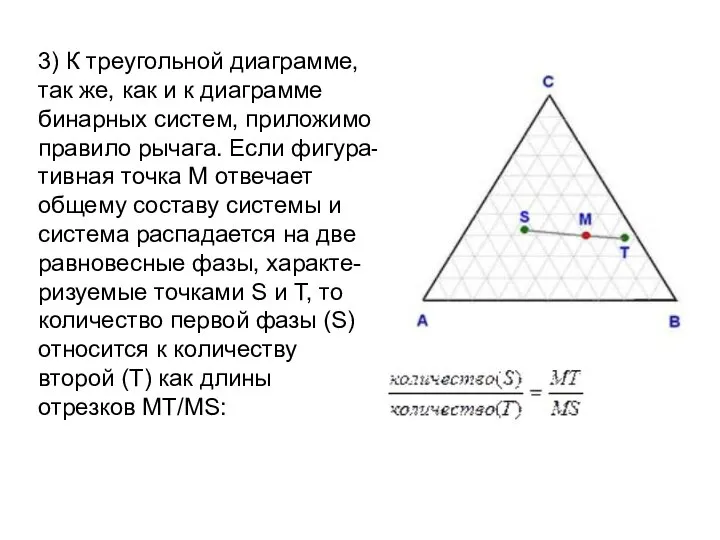
- 26. 3) К треугольной диаграмме, так же, как и к диаграмме бинарных систем, приложимо правило рычага. Если
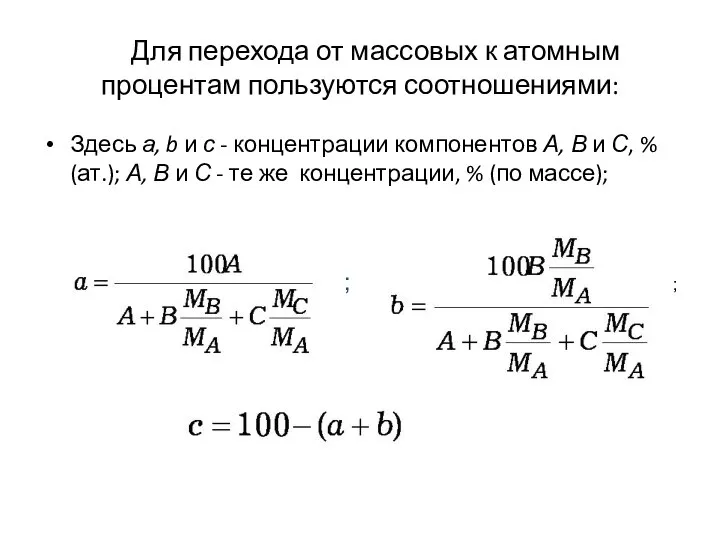
- 28. Для перехода от массовых к атомным процентам пользуются соотношениями: Здесь а, b и с - концентрации
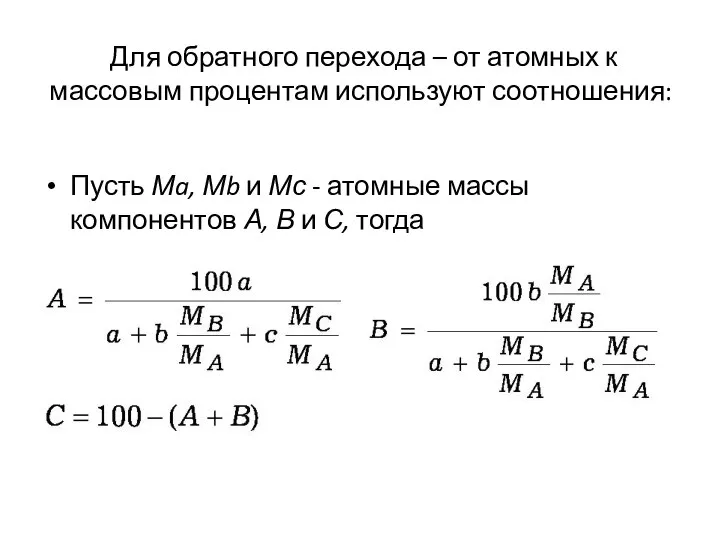
- 29. Для обратного перехода – от атомных к массовым процентам используют соотношения: Пусть Мa, Мb и Мс
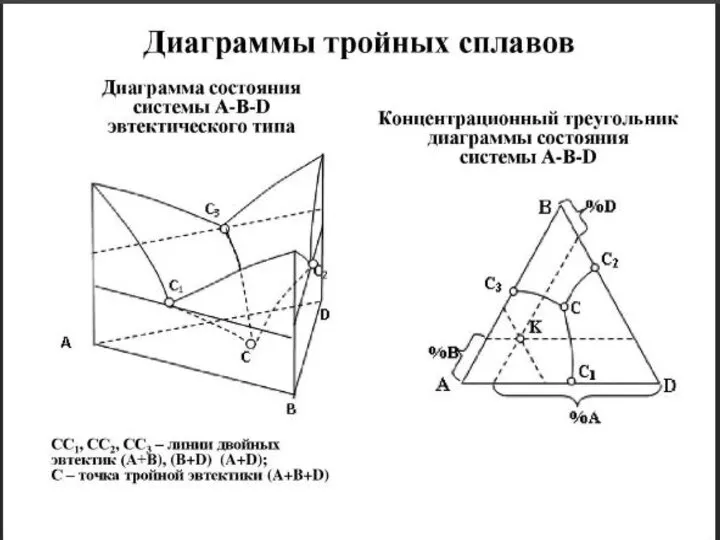
- 30. Диаграммы состояния тройных сплавов
- 31. Классификация диаграмм состояния тройных систем (ДСТС) а) Диаграммы состояния систем с неограниченной растворимостью компонентов в жидком
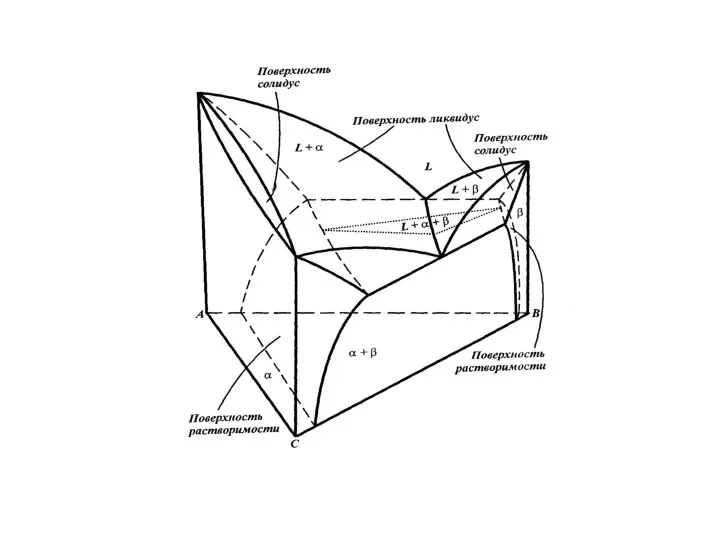
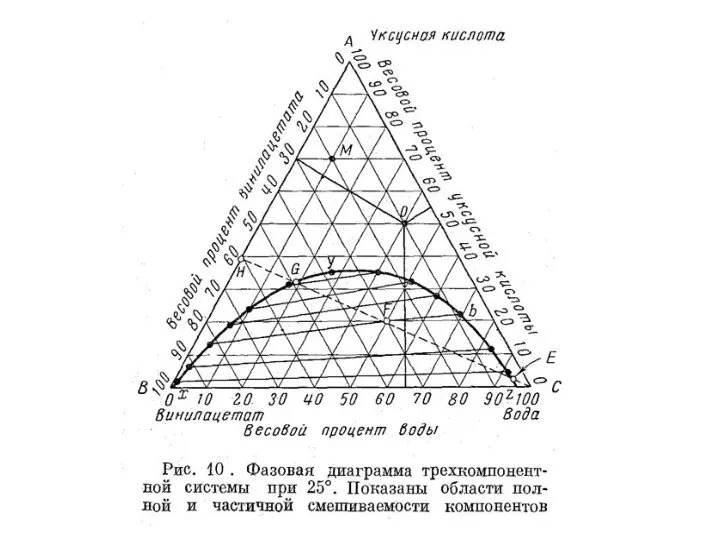
- 33. Общий вид тройных диаграмм состояния определяется характером двойных систем, образующих их боковые грани и характеризующих взаимодействие
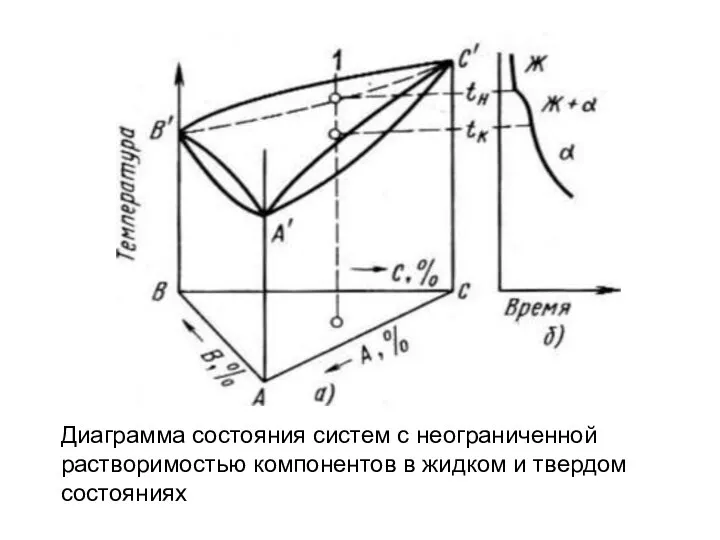
- 36. Диаграмма состояния систем с неограниченной растворимостью компонентов в жидком и твердом состояниях
- 37. Превращения в тройных сплавах удобнее наблюдать не по пространственной диаграмме, а по сечениям (разрезам) этих диаграмм.
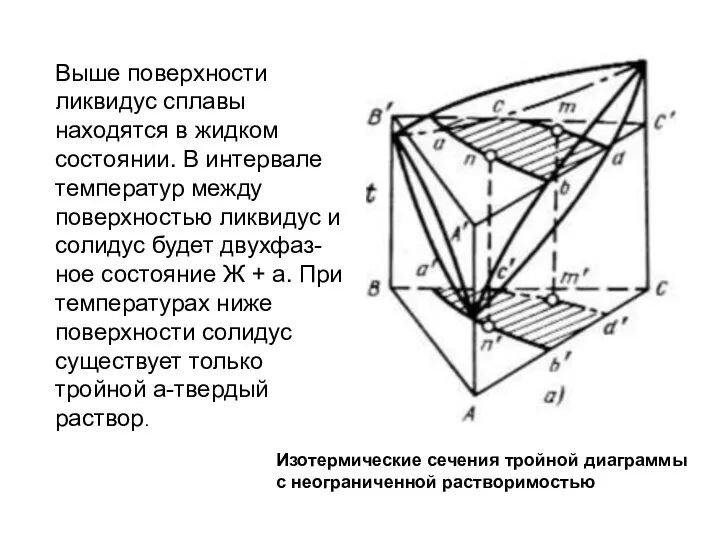
- 38. Выше поверхности ликвидус сплавы находятся в жидком состоянии. В интервале температур между поверхностью ликвидус и солидус
- 39. Жидкие растворы
- 40. Двухкомпонентные (жидкие) системы Рассмотрим диаграмму с учетом правила фаз: С=К-Ф+2. Если имеются два компонента, то С=4—Ф.
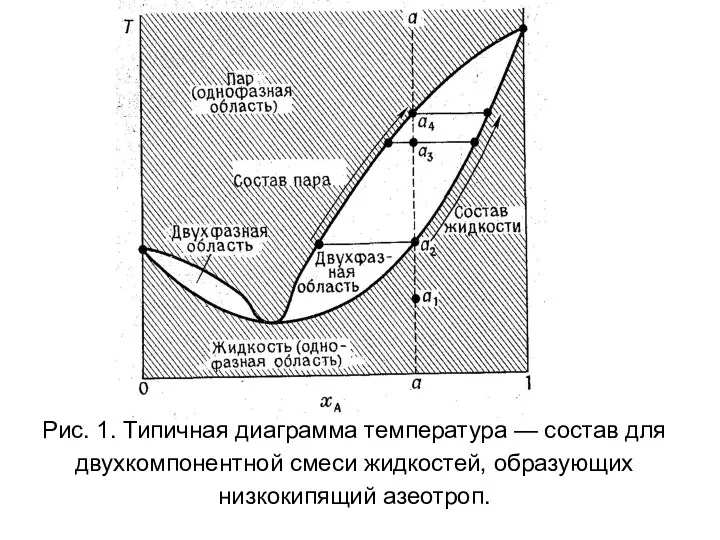
- 41. Рис. 1. Типичная диаграмма температура — состав для двухкомпонентной смеси жидкостей, образующих низкокипящий азеотроп.
- 42. Как интерпретировать диаграмму состав жидкости — состав пара. Типичная диаграмма для полностью смешивающихся жидкостей воспроизведена на
- 43. Вначале в точке а1 весь образец является жидкостью, и, поскольку оба компонента смешиваются, имеется только одна
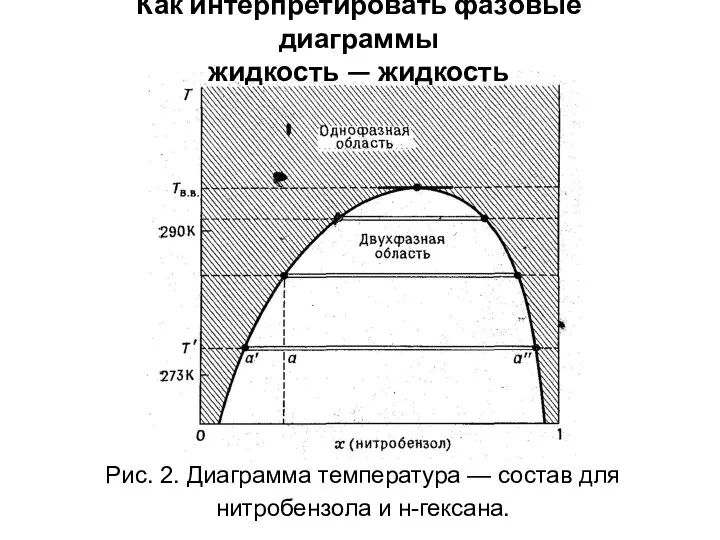
- 44. Как интерпретировать фазовые диаграммы жидкость — жидкость Рис. 2. Диаграмма температура — состав для нитробензола и
- 45. Здесь мы рассмотрим бинарные смеси (Ф=2) при таких температурах и давлениях, когда пар отсутс-твует. В частности,
- 46. Рассмотрим две частично смешивающиеся жидкости А и В. (подходящий пример: н-гексан и нитробензол). К образцу чистого
- 47. Если добавить еще больше нитробензола, то н-гексан переходит из слоя, богатого н-гекса-ном, в слой, богатый нитробензолом.
- 48. Изменение температуры влияет на концентрации, при которых происходит разделение фаз. В приведенном примере при повышении темпера-туры
- 49. Выше определенной температуры, называемой температурой взаиморастворения (сопsolute tеmpеrature), разделение фаз не происходит ни при каких концентрациях.
- 50. Может показаться совершенно естественным, что существует верхняя температура взаиморастворения, при которой более интенсивное молекулярное движение преобладает
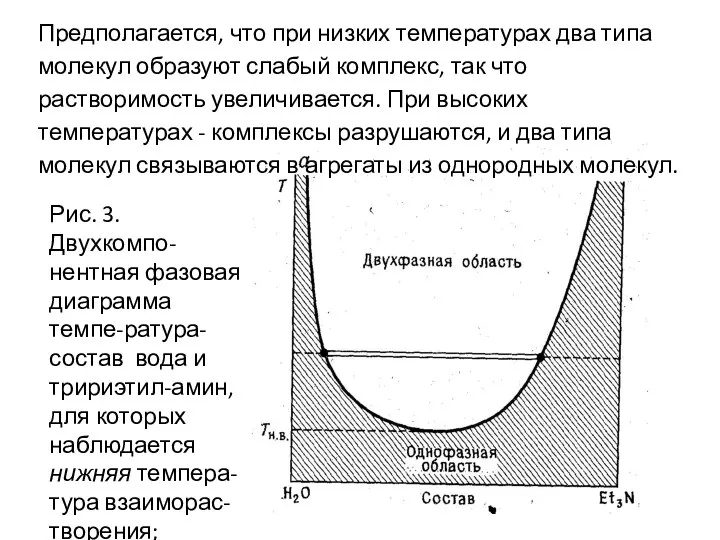
- 51. Предполагается, что при низких температурах два типа молекул образуют слабый комплекс, так что растворимость увеличивается. При
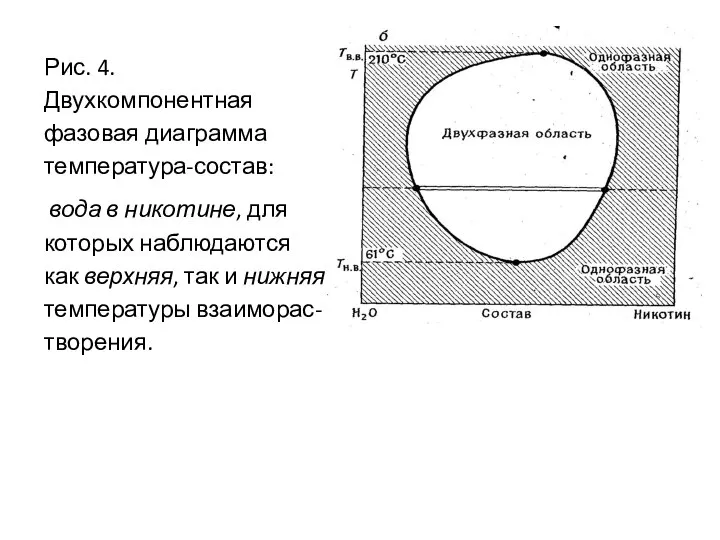
- 52. Для некоторых систем наблюдаются как верхняя, так и нижняя температуры взаиморастворения. Это обусловлено тем, что кинетическое
- 53. Рис. 4. Двухкомпонентная фазовая диаграмма температура-состав: вода в никотине, для которых наблюдаются как верхняя, так и
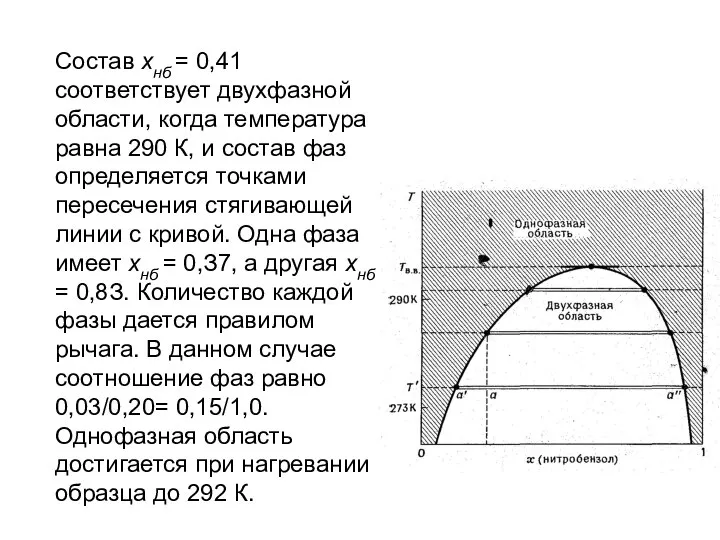
- 54. Пример 1. Смесь 50 г н-гексана и 50 г нитробен-зола приготовлена при 290 К. Каков состав
- 55. Состав хнб = 0,41 соответствует двухфазной области, когда температура равна 290 К, и состав фаз определяется
- 59. Скачать презентацию





















 Кремний и его соединения
Кремний и его соединения Циклоалканы или цикланы – циклические насыщенные углеводороды
Циклоалканы или цикланы – циклические насыщенные углеводороды Металлы. Общая характеристика ( 9 класс)
Металлы. Общая характеристика ( 9 класс) Типы химических реакций в неорганической химии
Типы химических реакций в неорганической химии Типы химических реакций. Реакции обмена
Типы химических реакций. Реакции обмена Спирты
Спирты Презентация на тему Законы электролиза
Презентация на тему Законы электролиза  Алкены
Алкены Chemia kosmetyczna
Chemia kosmetyczna Development of the system of concepts on the topic redox reactions in the school course of inorganic chemistry
Development of the system of concepts on the topic redox reactions in the school course of inorganic chemistry Теория химического строения органических веществ А.М. Бутлерова
Теория химического строения органических веществ А.М. Бутлерова Скорость химической реакции
Скорость химической реакции Строение комплексных соединений. Лекция 4
Строение комплексных соединений. Лекция 4 Чистые вещества и смеси. Использование химического анализа
Чистые вещества и смеси. Использование химического анализа Определение плотности газообразного вещества по плотности
Определение плотности газообразного вещества по плотности Решение заданий ОГЭ по химии (1 - 15)
Решение заданий ОГЭ по химии (1 - 15) Тайна алмазов
Тайна алмазов Исследование концентрированных заквасок для сметаны
Исследование концентрированных заквасок для сметаны Техника безопасности на уроках химии
Техника безопасности на уроках химии Адсорбция. Механизмы адсорбции. Термодинамика адсорбции. Лекция 5
Адсорбция. Механизмы адсорбции. Термодинамика адсорбции. Лекция 5 Аминокислоты
Аминокислоты Структура, свойства и термическая обработка железоуглеродистых сплавов
Структура, свойства и термическая обработка железоуглеродистых сплавов Изучение процесса замерзания воды
Изучение процесса замерзания воды Электрохимические процессы
Электрохимические процессы Расчет псевдокритических свойств конденсатного газа и пластовых газоконденсатных жидкостей. Анализ рекомбинированных проб
Расчет псевдокритических свойств конденсатного газа и пластовых газоконденсатных жидкостей. Анализ рекомбинированных проб Цинк (Zn). Свойства
Цинк (Zn). Свойства Тренинг по теме Валентность
Тренинг по теме Валентность Железо - основа всего мира
Железо - основа всего мира