Содержание
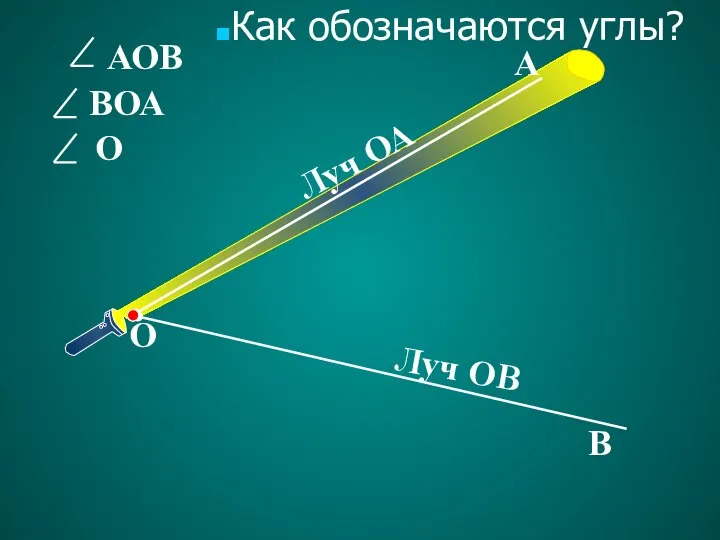
- 2. АОВ О В ВОА А О Луч ОА Луч ОВ Как обозначаются углы?
- 3. Для измерения углов используют транспортир . Какой инструмент можно использовать для измерения углов?
- 4. Единицы измерения угла Всего 180 частей. 1 часть – это 1 градус. 1/60 часть градуса называется
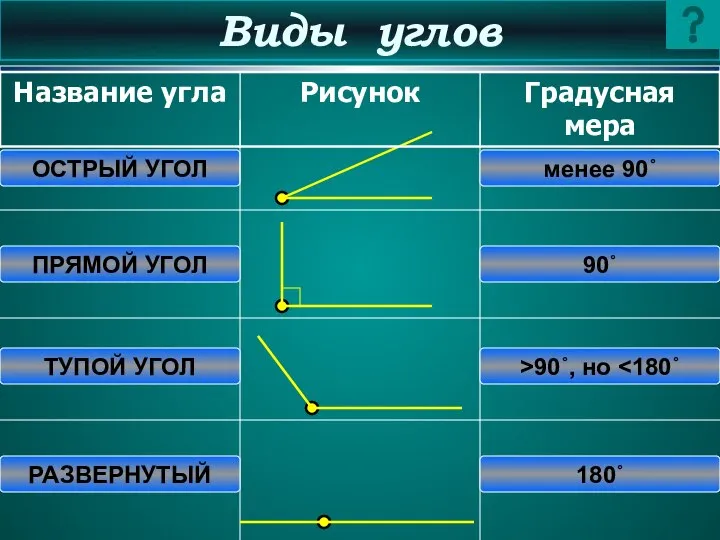
- 5. Виды углов ОСТРЫЙ УГОЛ ПРЯМОЙ УГОЛ ТУПОЙ УГОЛ РАЗВЕРНУТЫЙ менее 90˚ 90˚ >90˚, но 180˚
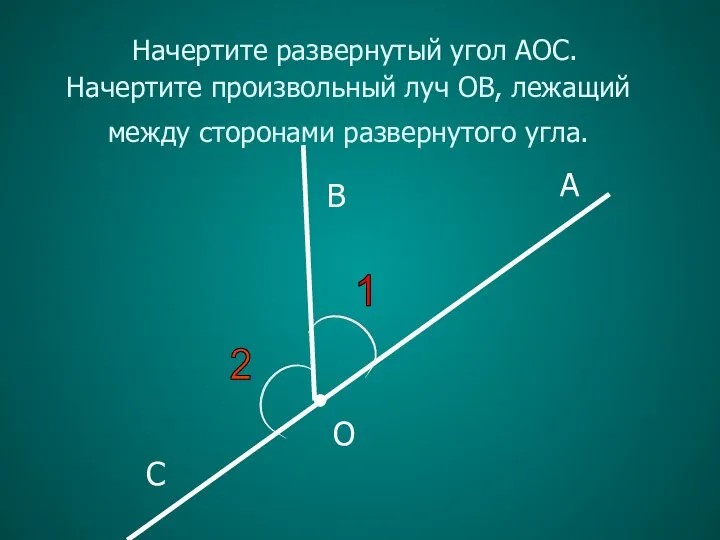
- 6. 1 A B C O Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий между сторонами
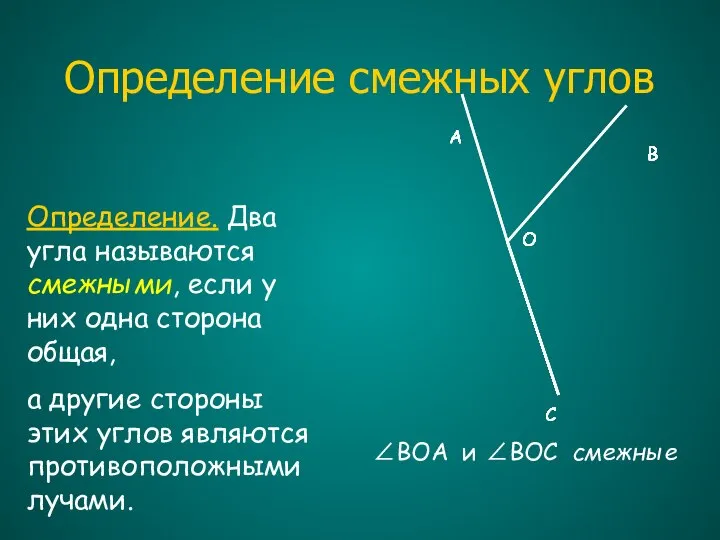
- 7. Определение смежных углов Определение. Два угла называются смежными, если у них одна сторона общая, а другие
- 8. Построение смежных углов
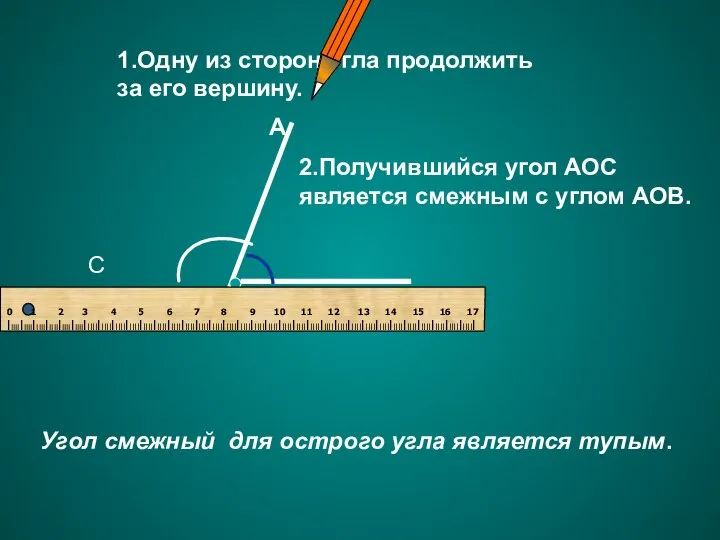
- 9. А О В С Угол смежный для острого угла является тупым. 1.Одну из сторон угла продолжить
- 10. 1. Одну из сторон угла продолжить за его вершину. 2. Получившийся угол АОС является смежным для
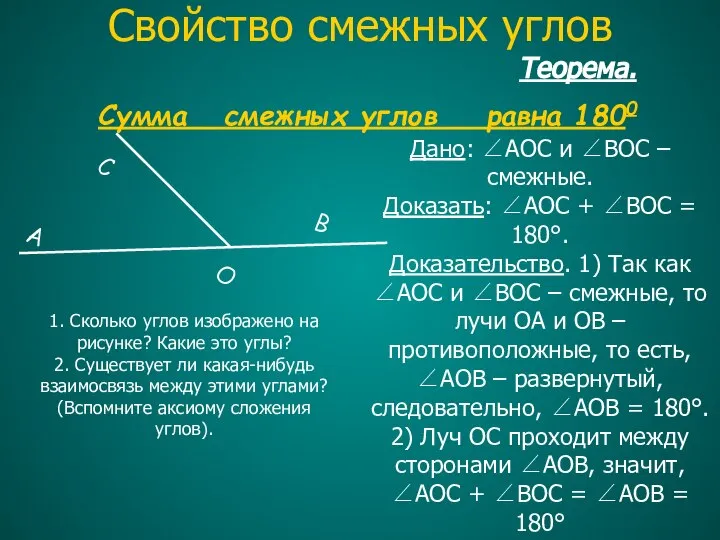
- 11. Теорема. Сумма смежных углов равна 1800 Дано: ∠AOC и ∠BOC – смежные. Доказать: ∠AOC + ∠BOC
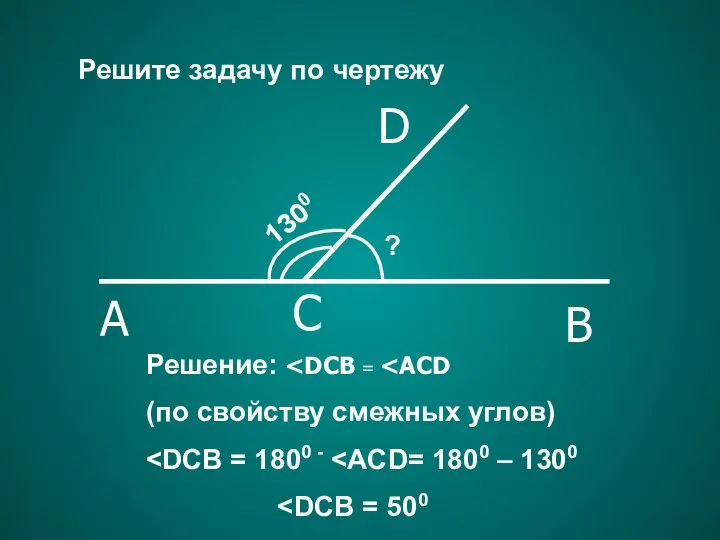
- 12. Решение: (по свойству смежных углов) Решите задачу по чертежу A C B D
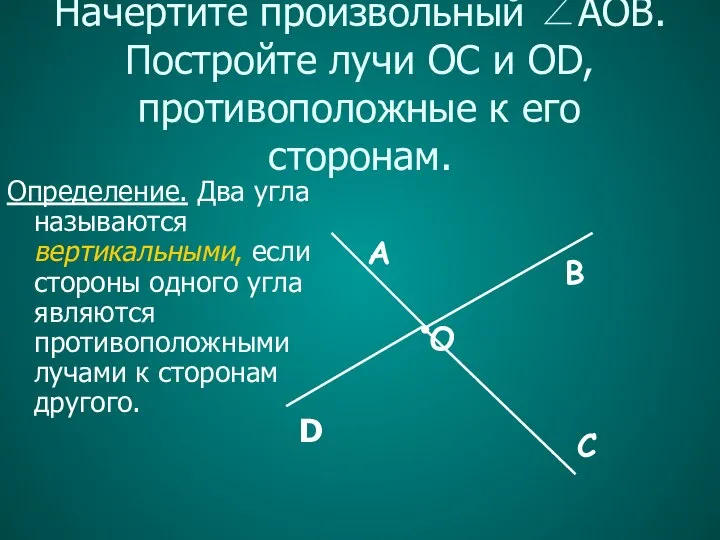
- 13. Начертите произвольный ∠AOB. Постройте лучи OC и OD, противоположные к его сторонам. В С D Определение.
- 14. Построение вертикальных углов
- 15. C D Построить угол. 2.Продлить каждую сторону угла за его вершину.
- 16. Свойство вертикальных углов Теорема. Вертикальные углы равны. Дано: ∠AOD и ∠COB – вертикальные. Доказать: ∠AOD=∠COB Доказательство.
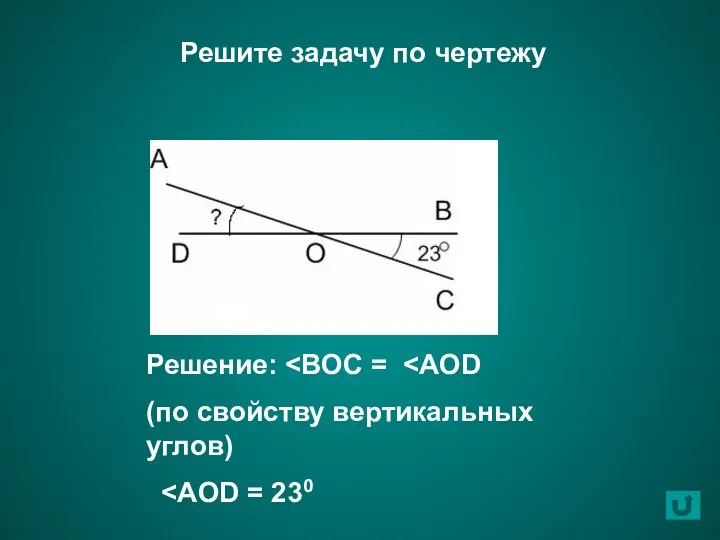
- 17. Решите задачу по чертежу Решение: (по свойству вертикальных углов)
- 19. Скачать презентацию







 Делимость целых чисел
Делимость целых чисел Состав числа в пределах 10; Компоненты задачи
Состав числа в пределах 10; Компоненты задачи Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Предел функции в точке
Предел функции в точке Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Объём цилиндра. Тест. Решение задач по готовым чертежам
Объём цилиндра. Тест. Решение задач по готовым чертежам Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Уравнение. Корень уравнения
Уравнение. Корень уравнения Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Предсказание будущего
Предсказание будущего Равнобедренный треугольник. Свойства равнобедренного треугольника
Равнобедренный треугольник. Свойства равнобедренного треугольника Угол. Прямой угол. Виды углов
Угол. Прямой угол. Виды углов Задача на спрос и предложение
Задача на спрос и предложение Алгоритм исследования функции
Алгоритм исследования функции Тренажёр Учим таблицу деления с удовольствием 3 класс
Тренажёр Учим таблицу деления с удовольствием 3 класс Презентация на тему Виды симметрии. Центральная и осевая симметрия
Презентация на тему Виды симметрии. Центральная и осевая симметрия  Системы принятия решений. Определения
Системы принятия решений. Определения Тренировочный блок по прикладной математике
Тренировочный блок по прикладной математике Классная работа. Признаки равенства треугольников
Классная работа. Признаки равенства треугольников Теоремы теории вероятностей
Теоремы теории вероятностей Симметрия относительно точки
Симметрия относительно точки Конспект урока по математике во 2 классе.
Конспект урока по математике во 2 классе. Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков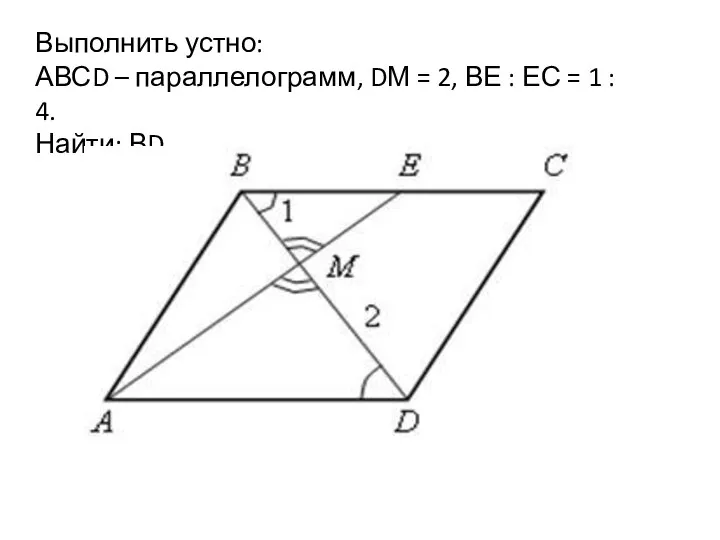 Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Математика в экономике
Математика в экономике Деление на 3
Деление на 3 Квадратное уравнение
Квадратное уравнение Презентация на тему Правильные многоугольники (9 класс)
Презентация на тему Правильные многоугольники (9 класс)